中2数学　2学期までのまとめ３－１

一次関数のグラフを振り返ろう！

グラフの問題は，数学の実力テストならいつだって大体出ます。

すぐに解けるよう，しっかり振り返っておきましょう！

授業動画です。

＜問題＞

次の問いに答えなさい。

（１）　グラフが（－１，３），（３，－５）を通る式を求めなさい。

（２）直線① \(x=3\) のグラフをかきなさい。

（３）直線② \(x-2y=4\) のグラフをかきなさい。

正解はこちら！

（１）　グラフが（－１，３），（３，－５）を通る式を求めなさい。

グラフ用紙を利用した例）

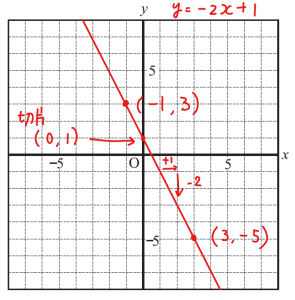
＜別解＞

（－１，３），（３，－５）を通るので，ｘの増加量とｙの増加量から求めてみよう。

\(\displaystyle 変化の割合(傾き)=\frac{ｙの増加量}{ｘの増加量}\)

を使うと，

\(\displaystyle 変化の割合(傾き)=\frac{-5-3}{3-(-1)}\)

\(\displaystyle 変化の割合(傾き)=-2\)

\(y=-2x+b\) と出るので，あとは（－１，３）を代入してしまおう。

\(3=-2×(-1)+b\)

\(b=1\)

よって，\(y=-2x+1\)

（２）直線① \(x=3\) のグラフをかきなさい。

縦か横か，ちょっと悩むかも！？

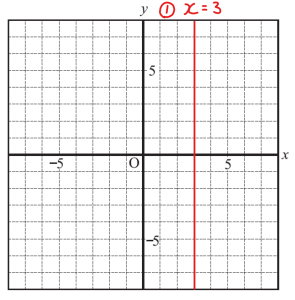
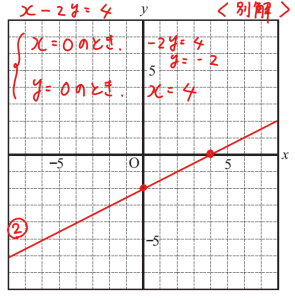
（３）直線② \(x-2y=4\) のグラフをかきなさい。

\(y=ax+b\)に直してグラフにします。

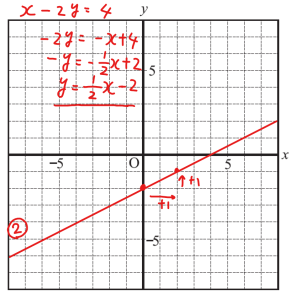
＜別解＞

ｘとｙが０のときの値を調べることで，

簡単にグラフ作成に必要な2点を知ることもできます。

おすすめ記事:

中2数学　2学期までのまとめ３ 中2数学　2学期までのまとめ５ 中2数学　2学期までのまとめ１－１ 中2数学　2学期までのまとめ１－２ 中2数学　2学期までのまとめ６ 中2数学　2学期までのまとめ６－１