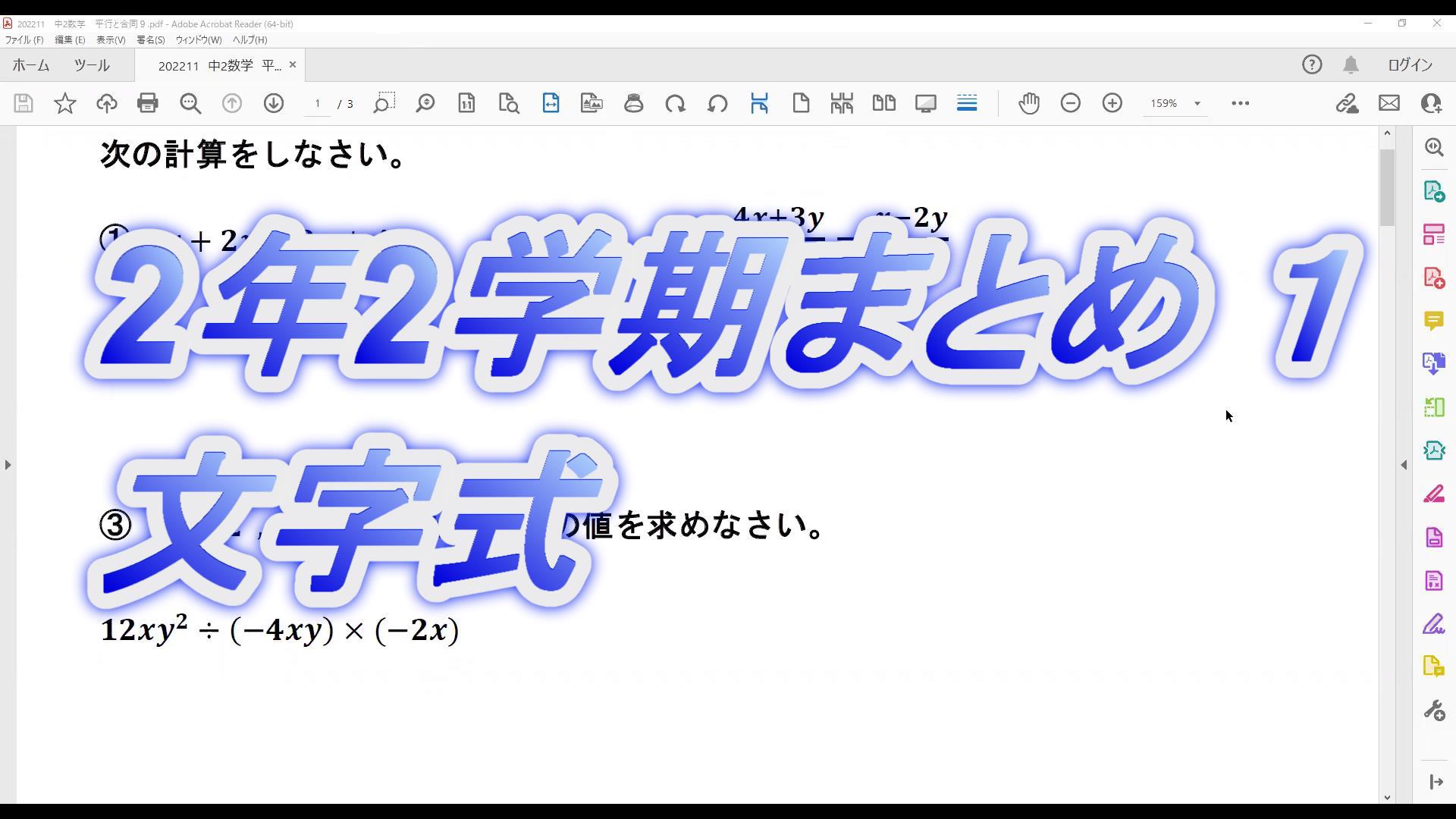
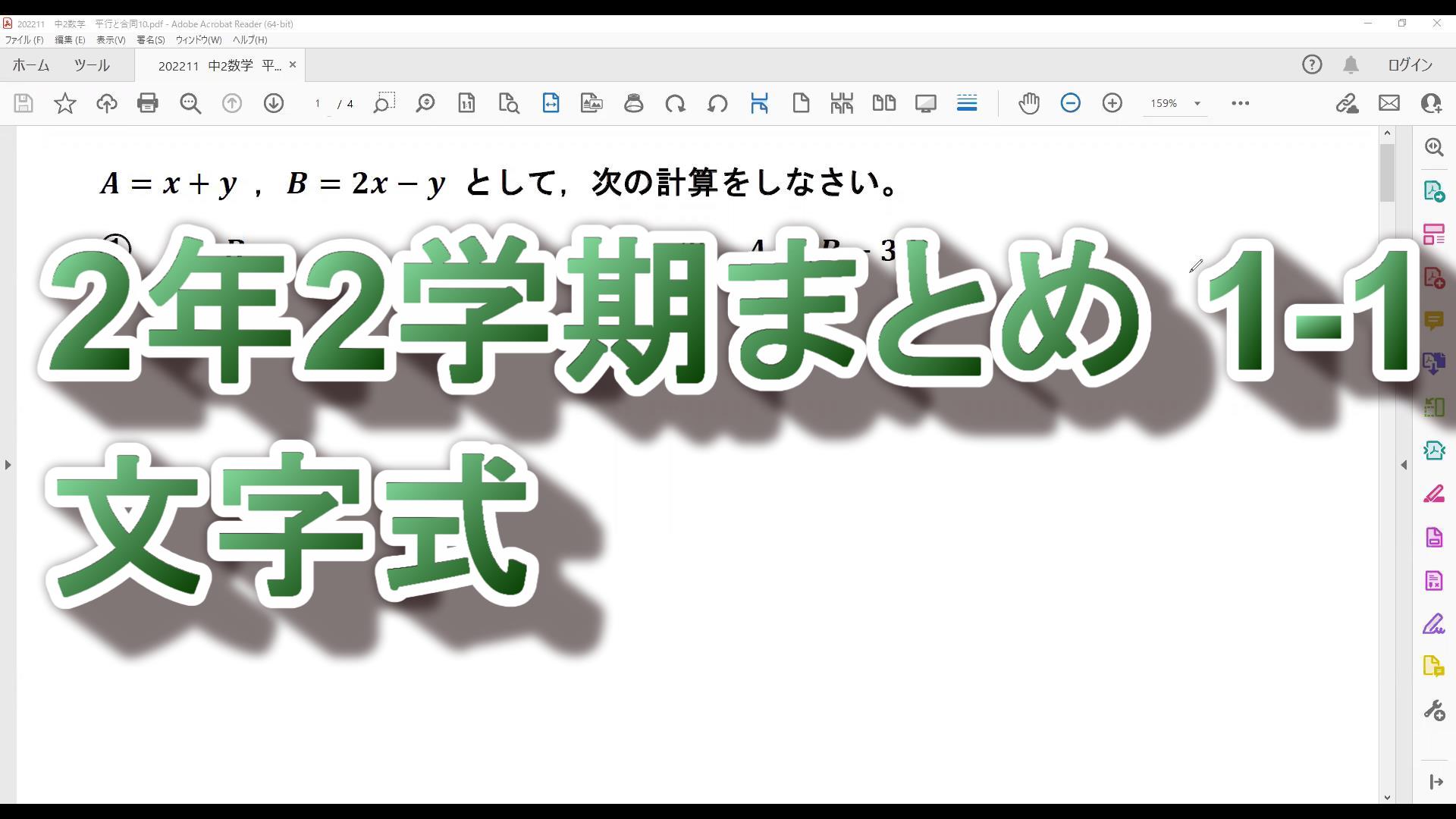
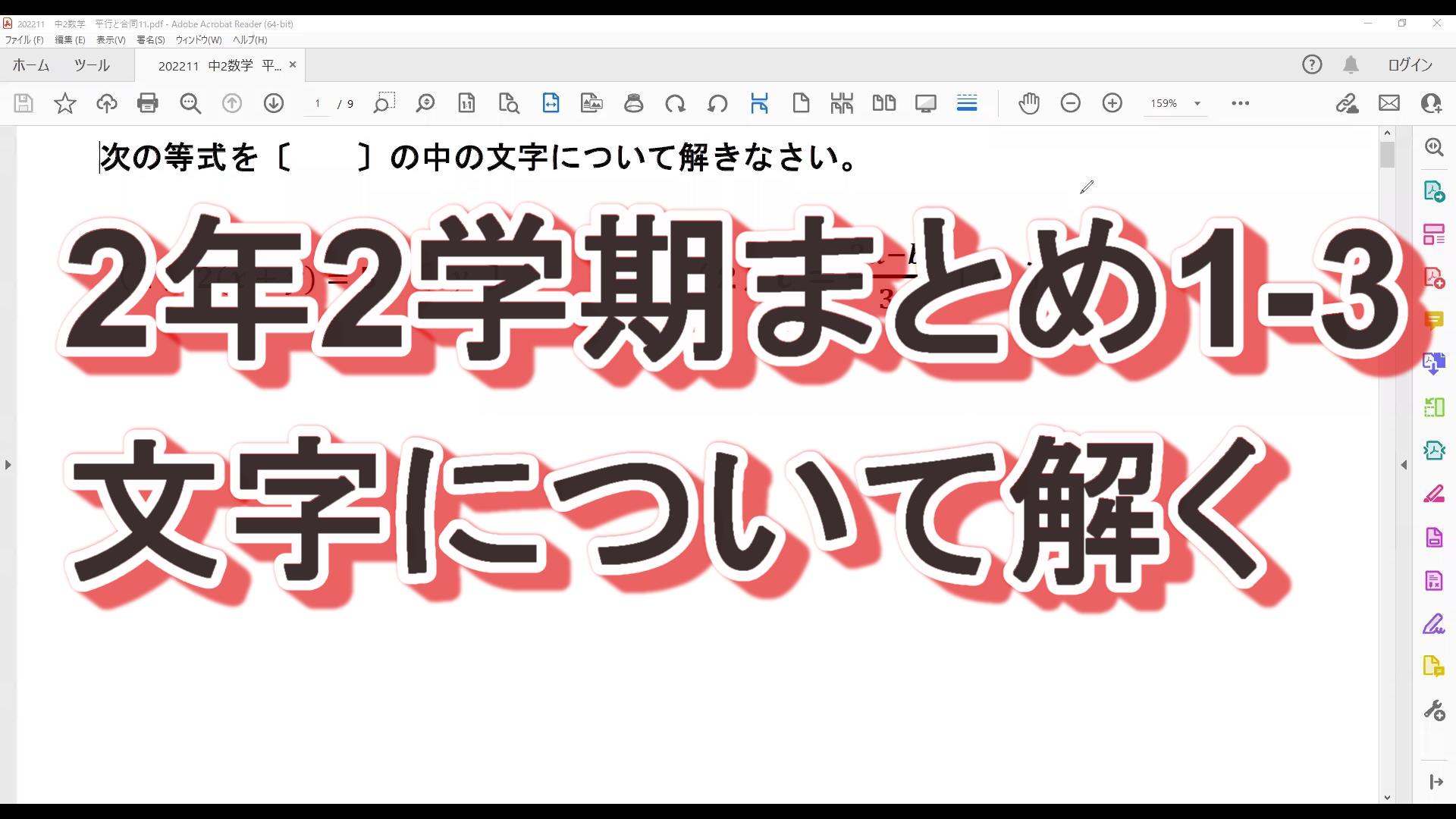
中2数学 2学期までのまとめ1-2
文字式で証明問題を復習しよう!
今回の授業動画です。
<問題>
3つ続いた整数の和は,3の倍数になる。このことを文字を使って説明しなさい。
例)1+2+3=6・・・3の倍数
2+3+4=9・・・3の倍数になるね!
正解はこちら!
生徒さんとの授業動画の1コマです。

3つ続いた整数は,整数nを使うと,
(nー1),n,(n+1)と表せる。
3つ続いた整数の和は,
(nー1)+n+(n+1)=3n
nは整数だから,3nは3の倍数である。
よって,3つ続いた整数の和は3の倍数になる。
※3つの整数を,n,n+1,n+2,と表してもOK!
その場合,和は3n+3=3(n+1)になります。
(n+1)は整数だから,3(n+1)は3の倍数になる,といった書き方にすればOK!
生徒さんと一緒に進めています。
解説動画をぜひ視聴してみてください。