一次関数のグラフを振り返ろう！
グラフの問題は，数学の実力テストならいつだって大体出ます。
すぐに解けるよう，しっかり振り返っておきましょう！
授業動画です。
＜問題＞
次の問いに答えなさい。
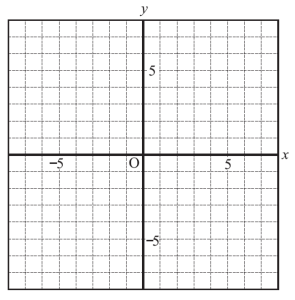
（１） グラフが（－１，３），（３，－５）を通る式を求めなさい。
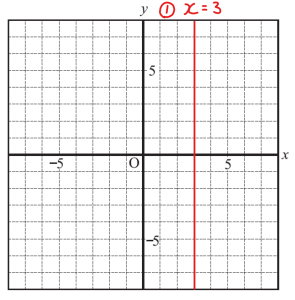
（２）直線① \(x=3\) のグラフをかきなさい。
（３）直線② \(x-2y=4\) のグラフをかきなさい。
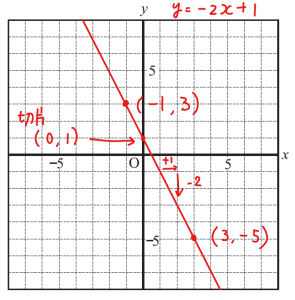
正解はこちら！
（１） グラフが（－１，３），（３，－５）を通る式を求めなさい。
グラフ用紙を利用した例）
＜別解＞
（－１，３），（３，－５）を通るので，ｘの増加量とｙの増加量から求めてみよう。
\(\displaystyle 変化の割合(傾き)=\frac{ｙの増加量}{ｘの増加量}\)
を使うと，
\(\displaystyle 変化の割合(傾き)=\frac{-5-3}{3-(-1)}\)
\(\displaystyle 変化の割合(傾き)=-2\)
\(y=-2x+b\) と出るので，あとは（－１，３）を代入してしまおう。
\(3=-2×(-1)+b\)
\(b=1\)
よって，\(y=-2x+1\)
（２）直線① \(x=3\) のグラフをかきなさい。
縦か横か，ちょっと悩むかも！？
（３）直線② \(x-2y=4\) のグラフをかきなさい。
\(y=ax+b\)に直してグラフにします。
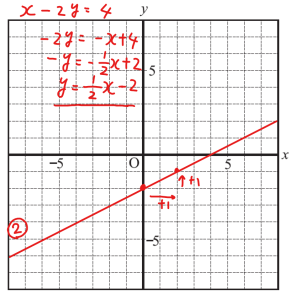
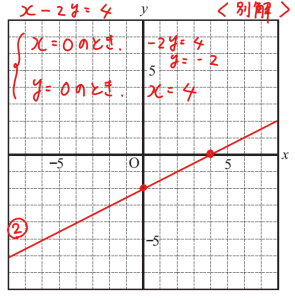
＜別解＞
ｘとｙが０のときの値を調べることで，
簡単にグラフ作成に必要な2点を知ることもできます。
レビューの平均
4.0
5つ星中4.0つ星です！（5人のお客様のデータ）
最高20%
良かった60%
ふつう20%
いまいち0%
最悪0%
お客様の声
たくさん、褒めていただきました！
学校の授業を安心して受けられるように、算数は予習中心で取り組みました。コーチに希望を伝えると、すぐに目標を設定してくれました。コーチからくるメッセージに息子も私も励まされました。
なりしん
丁寧に指導してくれます
うちの子は”させられる”ことが大嫌いなので、勉強をさせることができません。
アスミラではそんな子を無理に勉強させようなどとはせずに、日常の話などをしながら、できそうなタイミングで勉強に向かわせてくれているようです。
子どもが嫌いな勉強をやってみようと思える状態に導いてもらえることに満足しています。
横浜市民
通塾からアスミラへ
通塾していると遊ぶ時間が限られてしまい、通うのがめんどくさい。親がうるさいし…他人と比べたがるし、親の圧力が半端なかった。
アスミラへ入塾。先生と相談して苦手な所は一緒に授業で取り組んでくれたり、「ここは難しいよね。今は無理してやらなくていいよ」と言われた時は驚いたし、共感して貰えたことが嬉しかった。
本当に逃げていいのかなぁと心配になってしまったこともあったが、遠回りして解ける時期が来たら、先生が再度「前、無理してやらなくていいよって言った所、覚えてる？今ならチャレンジ出来るからやってみない？」と
自分にあったペースで目標設定を相談出来る所がありがたい。
先生のおかげで親に、私の思ってることを代弁してくれたり、取り持ってくれてありがとうございます。
ヒラヤマ山脈
褒めてくれる場所
子供の学習に対して、学年が上がるにつれて親も焦り不安になり、出来て当たり前と褒めることを忘れ…出来ないことばかり目に入り、怒ってしまい悩んでおりました。
授業を拝見すると、「ここの単元が出来ないわけではなく、その前の○○の理解が出来てないので一緒に解いてみる？それとも復習入れとくから取り組んで見てね。」と先生から言われて、つまづきを分かりやすくアドバイスいただけるので親も納得。
次回の授業迄に取り組んだ我が子に驚き、更に先生から褒めて貰えて嬉しそうな我が子を見られてホッコリ。
先生は子供目線の言い分、大人目線での言い分を取り持っていただきながら、我が子に響く声掛けと親の安定剤になっていただいております。
もも
親と子どもの間を取り持ってくれています
大波先生は独特の話し方で変に顔色を伺うことなく話ししてくれるようで、先生臭くなく、子どもも話しくらいしてもいいかと気を許しているのかなと思います(えらそうですみません)。
たくさん書きたいことはありますが、くどくなるのでこの辺までにとどめます。
本当は星５つ付けたいところですが、まだ上がる余地を残すという意味で星４つ。
こば犬
