確率　テスト対策３　２つのさいころの問題

さいころの確率　「少なくとも」という語句が入った問題

今回のオンライン個別指導動画はこちら！

次の問題にチャレンジしてみよう！

2問あるよ！

＜問題＞

大小２つのさいころを同時に投げるとき，次の確率を求めなさい。

ただし，どの結果が起こることも同様に確からしいとする。

（３）少なくとも１つは５の目が出る確率を求めよう！

（４）少なくとも１つは偶数である確率を求めよう！

便利なさいころ表，ぜひみなさんも表を書いて解いてみよう！

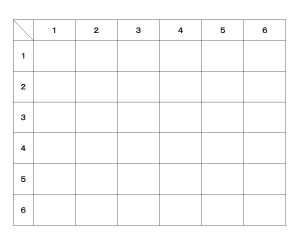
正解はこちら！

（３）少なくとも１つは５の目が出る確率を求めよう！

こたえ　\(\displaystyle \frac{11}{36}\)

５さえ入っていればOK。

大さいころが５，小さいころ５の「ぞろ目」ももちろんOKです。

全部で11通り。

（４）少なくとも１つは偶数である確率を求めよう！

こたえ　\(\displaystyle \frac{3}{4}\)

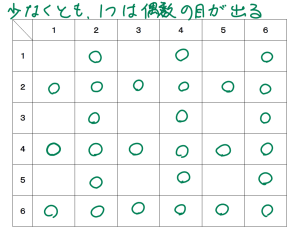
大小さいころ，どちらかに偶数が入っていればOKです。２，４，６ですね。

もちろん，（２，２）（４，４）（６，６）の「ぞろ目」もOKです。

全部で27通りあります。

＜別解＞

ここで，先ほどの表の残りに注目します。

カウントしていない部分に★マークを付けました。

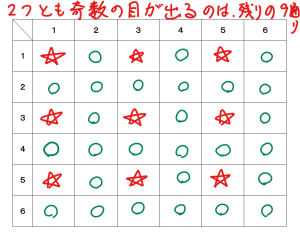
★マークは全て，大小のさいころが２つとも奇数のパターンです。

つまり，「少なくとも1つは偶数」のパターンを探したい場合，２つとも奇数のパターンを探して全体の１００％からひくというのも正解。

２つとも奇数のパターンは全36通り中で9通りあります。

よって，

\(\displaystyle 1-\frac{9}{36}\)

\(\displaystyle =\frac{27}{36}\)

\(\displaystyle  =\frac{3}{4}\)

ぜひオンライン授業動画も視聴してみてください！

おすすめ記事:

確率　テスト対策１　２つのさいころの問題 確率　テスト対策２　２つのさいころの問題 確率の問題５　くじびき　前編 確率の問題６　くじびき　後編 グループ作りの問題　組み合わせは何通り？　前編 確率　テスト対策７　カードを２枚選ぶ問題