応用編！式による証明にチャレンジしてみよう！　３

応用編！　式による証明にチャレンジしよう！３

 

 

 

次の問題にチャレンジしてみよう！

 

＜問題＞

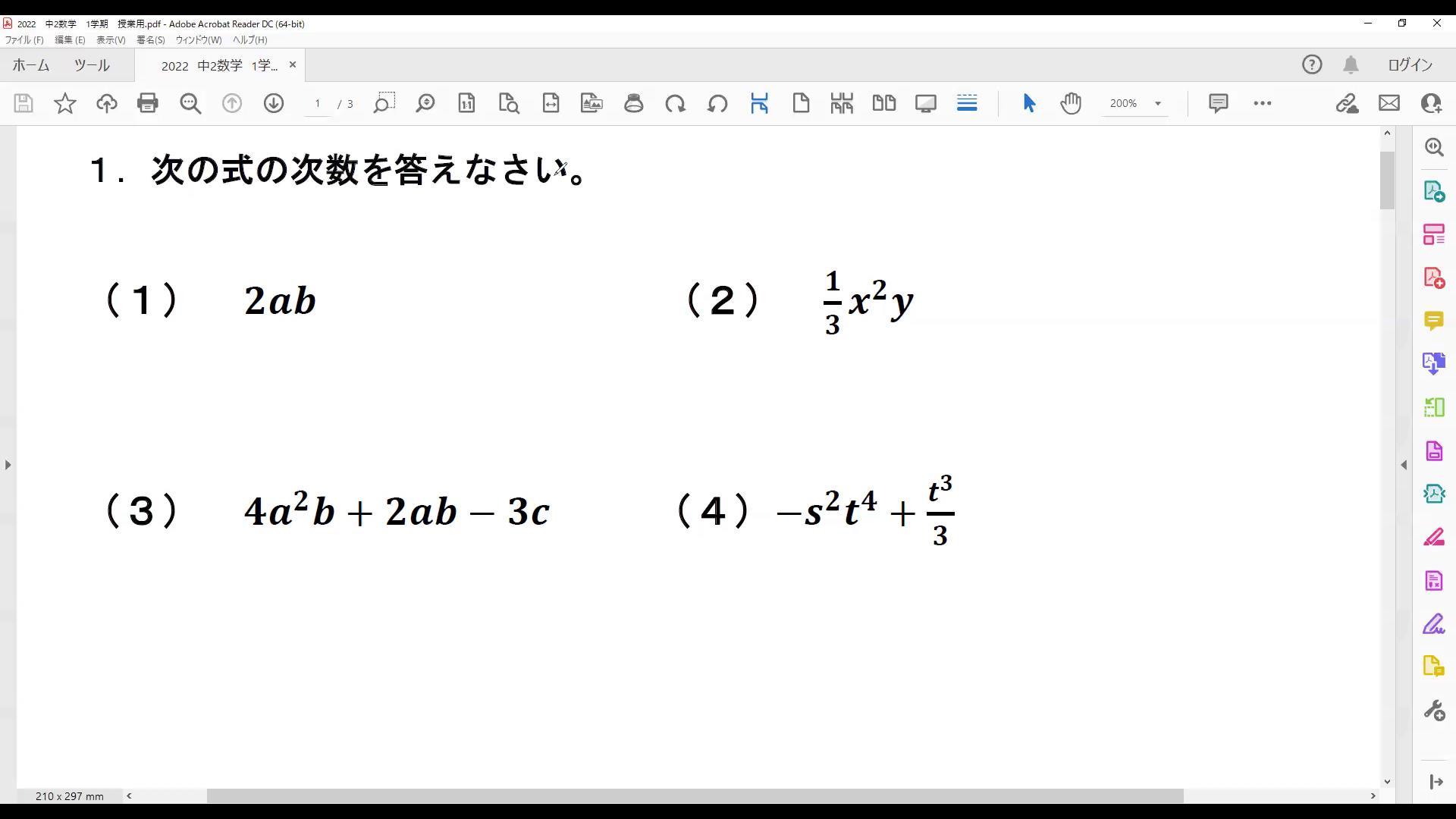
2けたの自然数と，その数の一の位と十の位の数字を入れかえた数の和は，11の倍数になることを説明しなさい。

 

（　　）にあてはまる式を入れていこう！

 

はじめに考えた数の十の位を\(x\)，一の位を\(y\)とすると，

はじめの数は（　　　　　　　　　）

入れかえた数は（　　　　　　　　　）と表される。

 

それらの和は，

（　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　）

 

（　　　　　　　）は整数だから，（　　　　　　　　　）は11の倍数である。

したがって，2けたの自然数と，その数の一の位と十の位の数字を入れかえた数の和は11の倍数になる。

 

 

例えばということで，2けたの自然数を35とすると・・・・。

一の位と十の位を入れかえると53。

35＋53＝88　　たしかに11の倍数になりそうですね。

 

これを文字を使って説明していくという問題です。

 

 

正解はこちら！

 

＜問題＞

2けたの自然数と，その数の一の位と十の位の数字を入れかえた数の和は，11の倍数になることを説明しなさい。

 

（　　）にあてはまる式を入れていこう！

 

はじめに考えた数の十の位を\(x\)，一の位を\(y\)とすると，

はじめの数は（　\(10x+y\)　）

入れかえた数は（　　\(10y+x\)　）と表される。

 

それらの和は，

（　　\((10x+y)+(10y+x)=11(x+y)\)　　　）

 

（　　\((x+y)\)　　）は整数だから，（　　\(11(x+y)\)　　）は11の倍数である。

したがって，2けたの自然数と，その数の一の位と十の位の数字を入れかえた数の和は11の倍数になる。

 

 

 

 

解説動画はこちら！

生徒さんとの授業動画になります。4分30秒です。

一緒に学習してみてください！