7/21(月)までの限定3名様☆
夏期講習の体験会やってます!
オンライン秘密特訓で
逆転したい生徒さん,集まれ!
「もうどうしたらいいの!?」
そんなキミこそチャンスだ!
保護者の方からお申込みください。

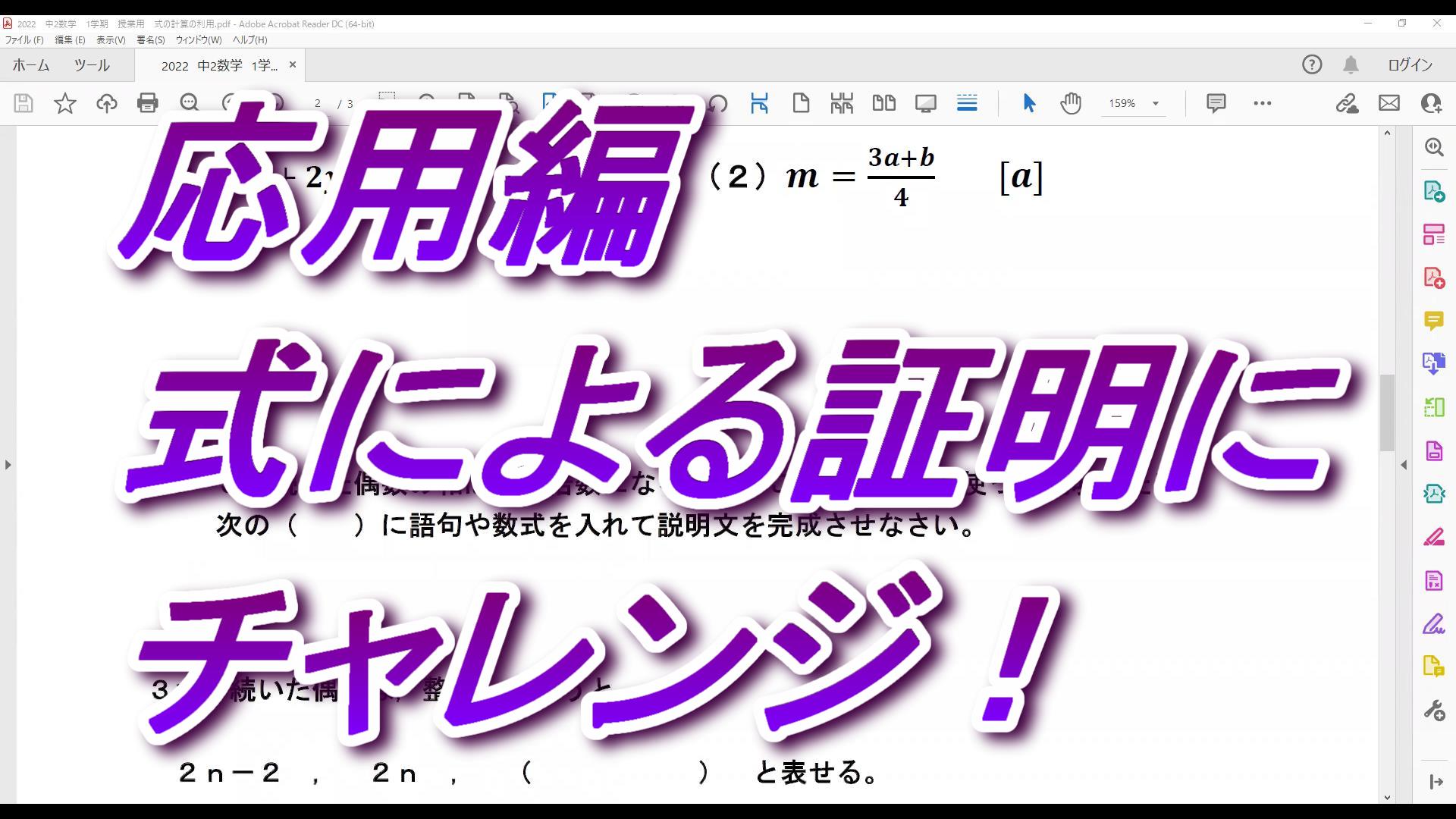
応用編! 式による証明にチャレンジしよう!その2

次の問題にチャレンジしてみよう!
<問題>
2つ続いた奇数の和は4の倍数になる。このことを文字を使って説明しなさい。
例えば,
3+5=8
11+13=24
たしかに,4の倍数になりそうです。これを文字を使って説明する問題です。
<ヒント>
偶数は整数nを使うと2nで表せるよ!
奇数は偶数の隣にあるから,2nー1 または 2n+1 だね!
正解はこちら!
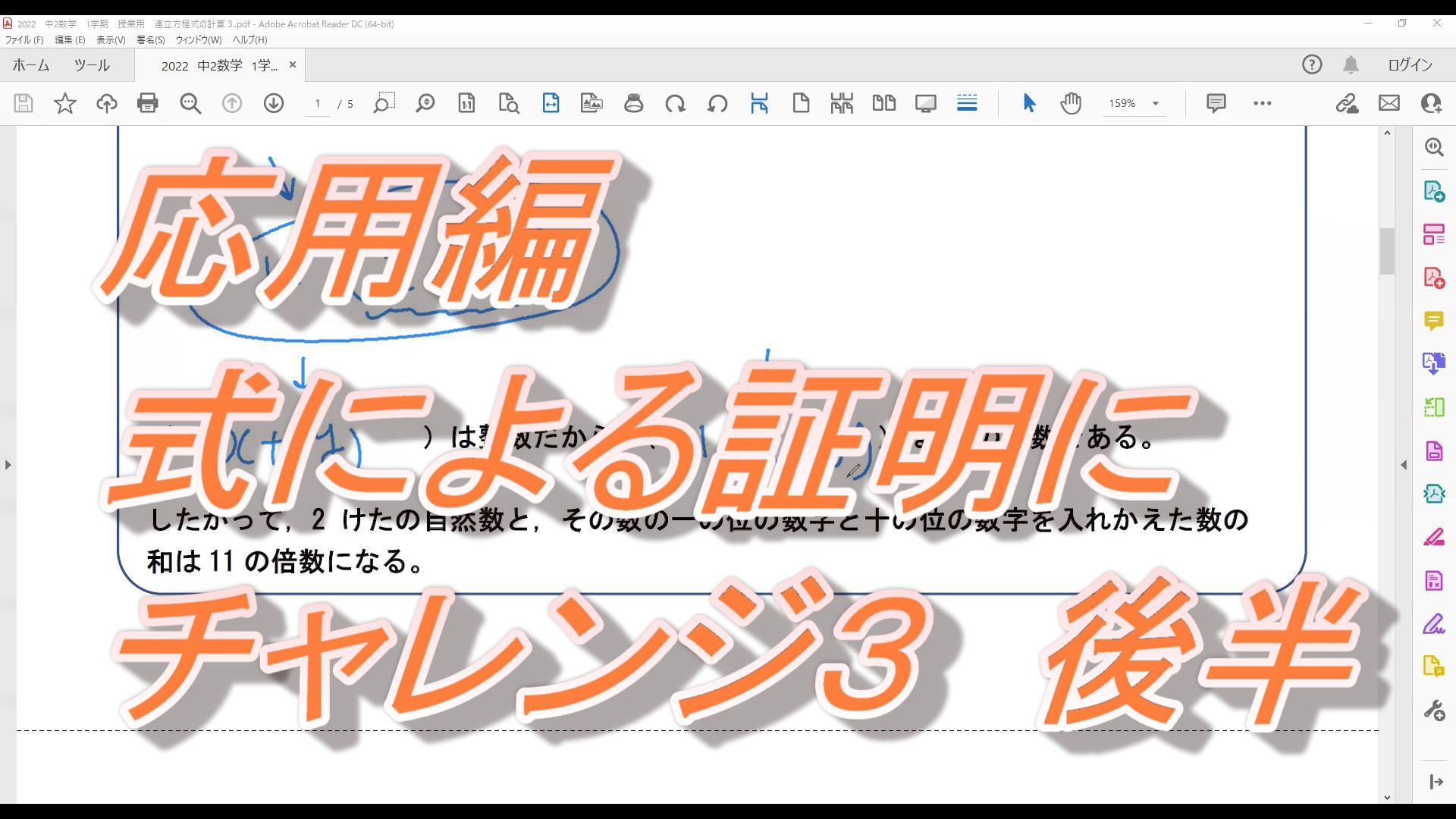
<問題>
2つ続いた奇数の和は4の倍数になる。このことを文字を使って説明しなさい。
整数nを使うと,2つ続いた奇数は,2n-1,2n+1 と表せる。
その和は, (2n-1)+(2n+1)=4n
nは整数だから,4nは4の倍数である。
したがって,2つ続いた奇数の和は4の倍数になる。 (終わり)
実際の授業の様子
生徒さんとの個別オンライン授業の様子です。けっこう生々しい2分10秒の切り抜き動画です。
動画で一緒に学びながら取り組んでみてください。
レビューの平均
4.4
5つ星中4.4つ星です!(190人のお客様のデータ)
最高71%
良かった14%
ふつう4%
いまいち3%
最悪8%
お客様の声
理解できスギィ
理科が苦手な自分にとっては最高だってはっきりわかんだね。
もっと理科の問題を発信してほしいゾー
364364
アスミラからの返信
理科かあー,リクエストありがとうございます。
わかりやすい!!
自分は社会がすごく苦手だけど、
わかりやすくまとめられているので、
とてもわかりやすいです!
これからも、このサイトを使って勉強したいです!!
実力テストがんばります!!
A
アスミラからの返信
コメントありがとうございます。
社会のテスト対策って難しいけど,楽しくやった者勝ちなところあるから応援してます。
やばい
あ
アスミラからの返信
説明が下手で申し訳ないです…。
できれば,どの問題だったか教えていただけないでしょうか・・・。
意外といけた
アタオカ
アスミラからの返信
コメントありがとうございます。
これからも自信をもって取り組んでくれい!
わかりやすい解説
めっっっっちゃ
わかりやすいッッッッ
テスト頑張りやす。
スマイル君
アスミラからの返信
コメントありがとうございます。
1学期期末テストかな,がんばれ!
よかった
問題も比較的解きやすかった。
苦手が克服できそうかも…?
lonelylonely
アスミラからの返信
誰にでも苦手はあるので,無理に克服しなくても良いかと。
苦手にチャレンジできること自体がすごい!
頑張ってできた!
難しかったけどなんとか解けましたー!
テスト頑張る!
まろ
アスミラからの返信
何やらすごい意欲を感じるコメントだ!
応援しています!
Very good
あひるの子
アスミラからの返信
コメントありがとうございます。
私のオンライン個別指導もぜひご検討くださーい。
難しいと思っていた
難しいと思っていた地理が意外と簡単でおもしろかったです
今後も利用します!
寝る月
アスミラからの返信
地理っておもしろいよね!
これからもがんばってね!
trash
math
アスミラからの返信
ゴミ呼ばわりなんてひどい☆
ただ気になるのは,このコメント書いているとき,この人はどんな気分だったんだろうかと。ツライことでもあったんだろか。