
今回は中3の二次関数の応用問題を
特集します。
グラフ問題は,
実力テストや高校入試レベルでは
ほぼ出ますよね。
今回の問題も,
けっこうあるあるなタイプです。
見たことある受験生も多いのではと。
それでは早速いってみよー!
二次関数の応用問題チャレンジ
次の問題にチャレンジしてみてね。
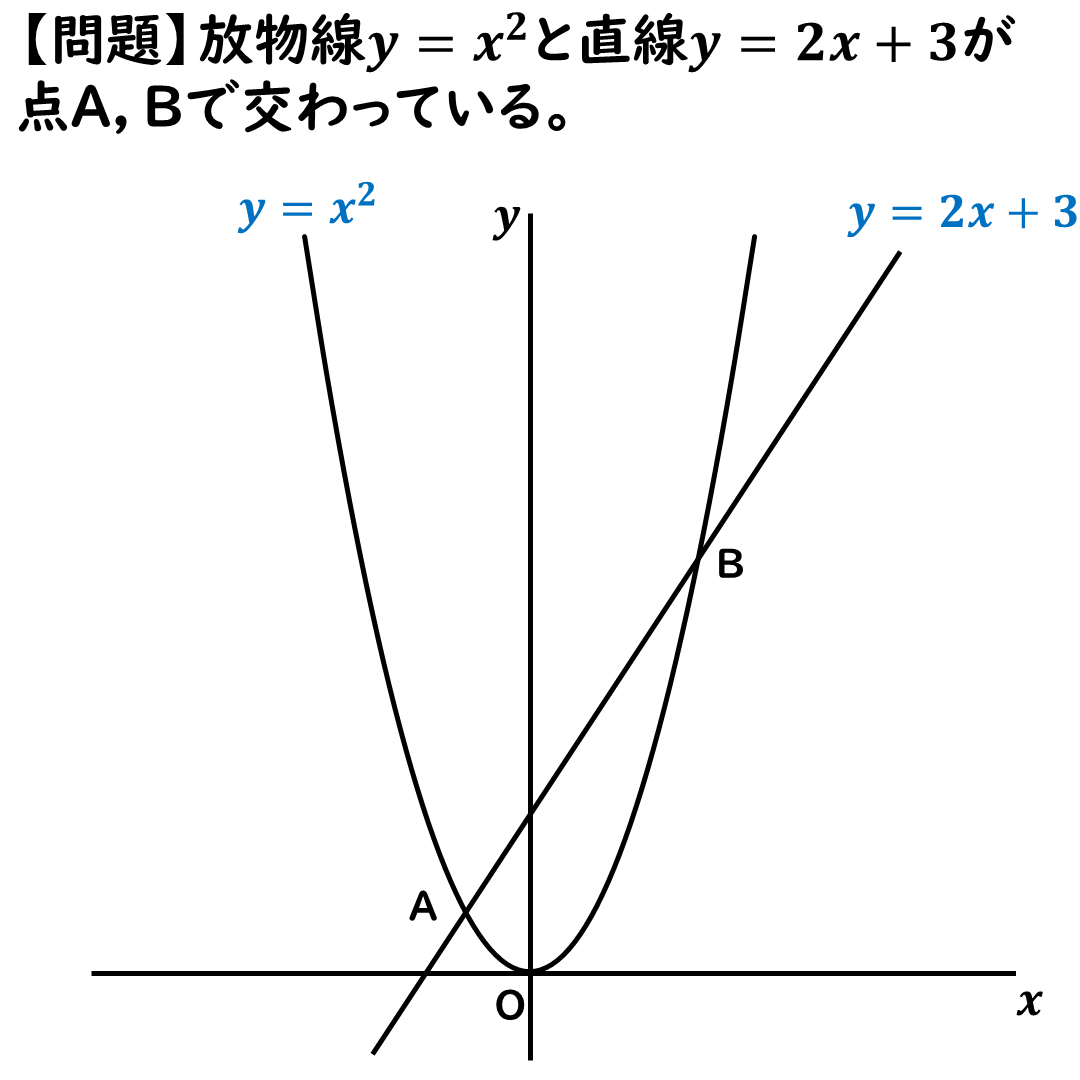

こたえはすぐ下に出しますが,
まずは自分で考えてみてね。
答えとヒント
それでは,答えとヒントを
出しますね。
こんな感じで,
y=2x+3の平行線をひいて,
△OABと同じ面積の三角形を
作っていくよ。
今回は,
△OABの面積を求める必要はない。
点A,点Bの座標も
求める必要ないよ。
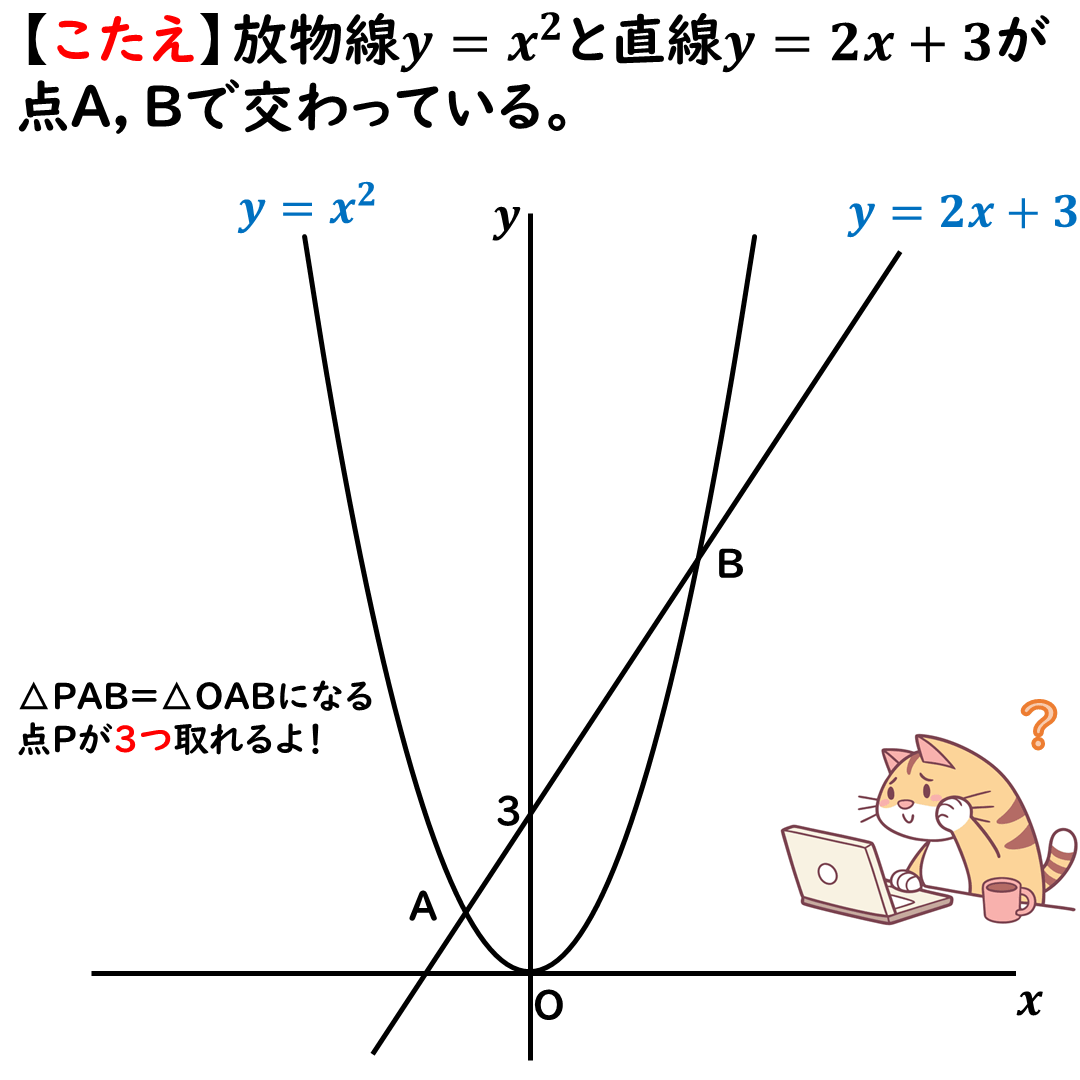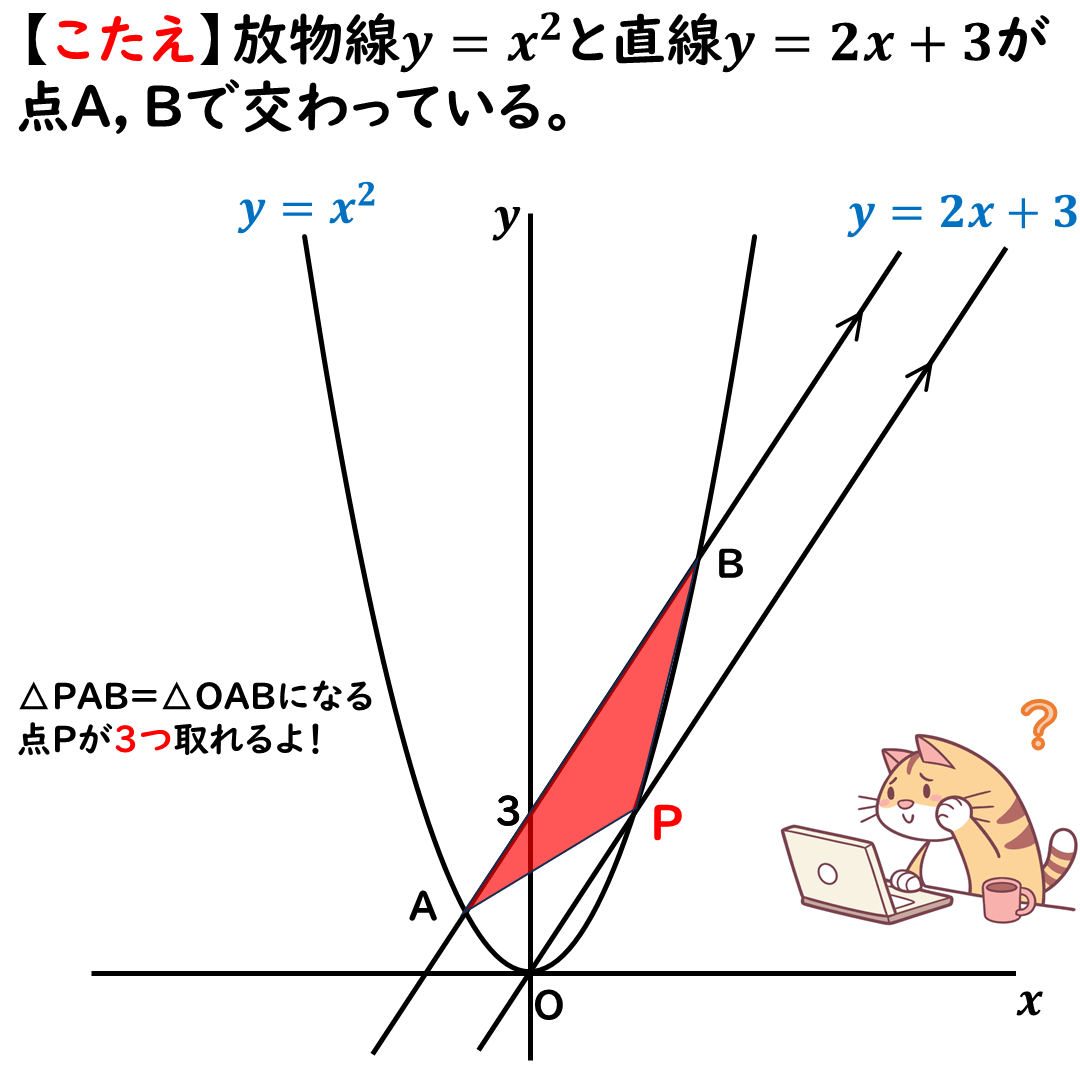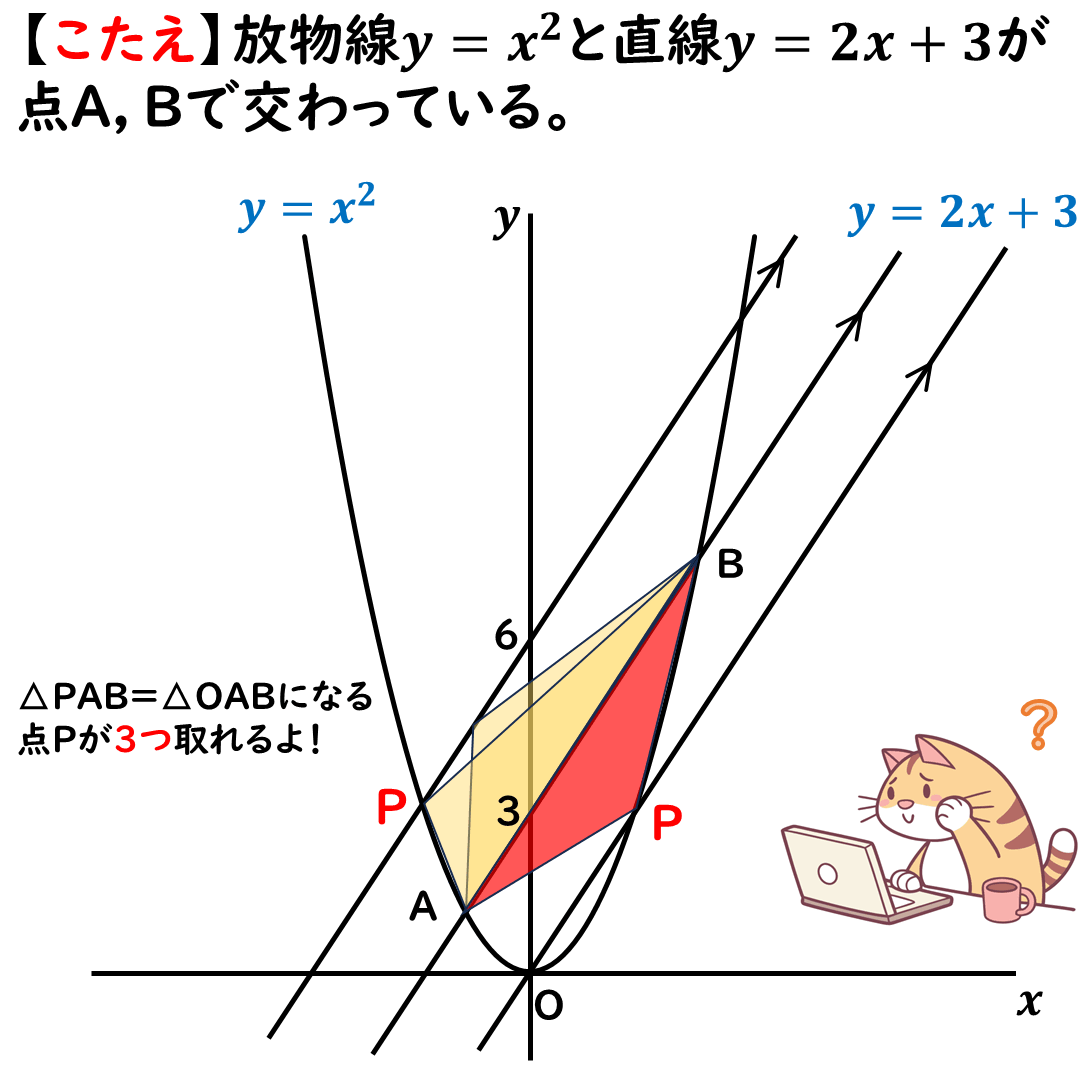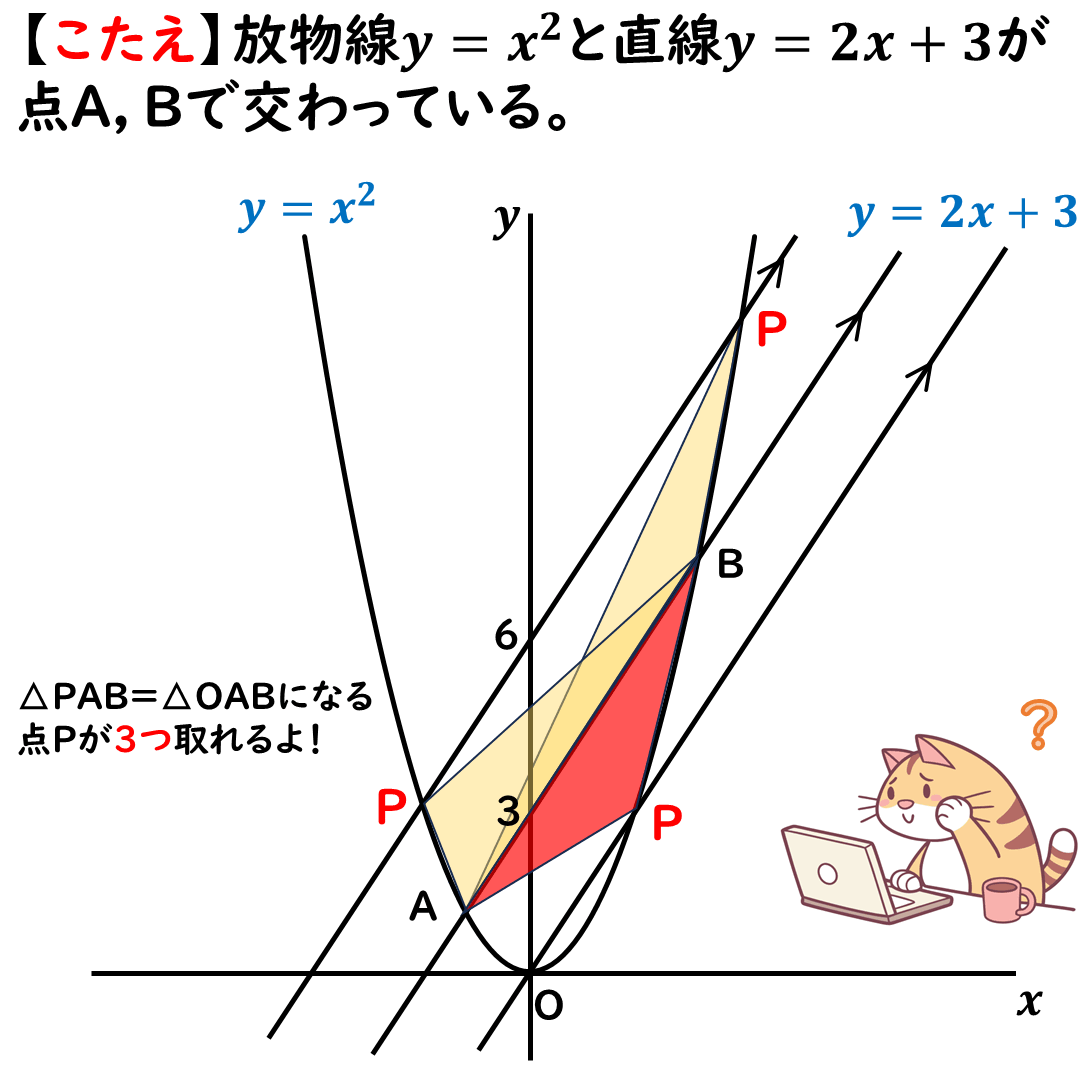
そうすると,
次の画像のように,点Pは
3ヶ所取れるよ。
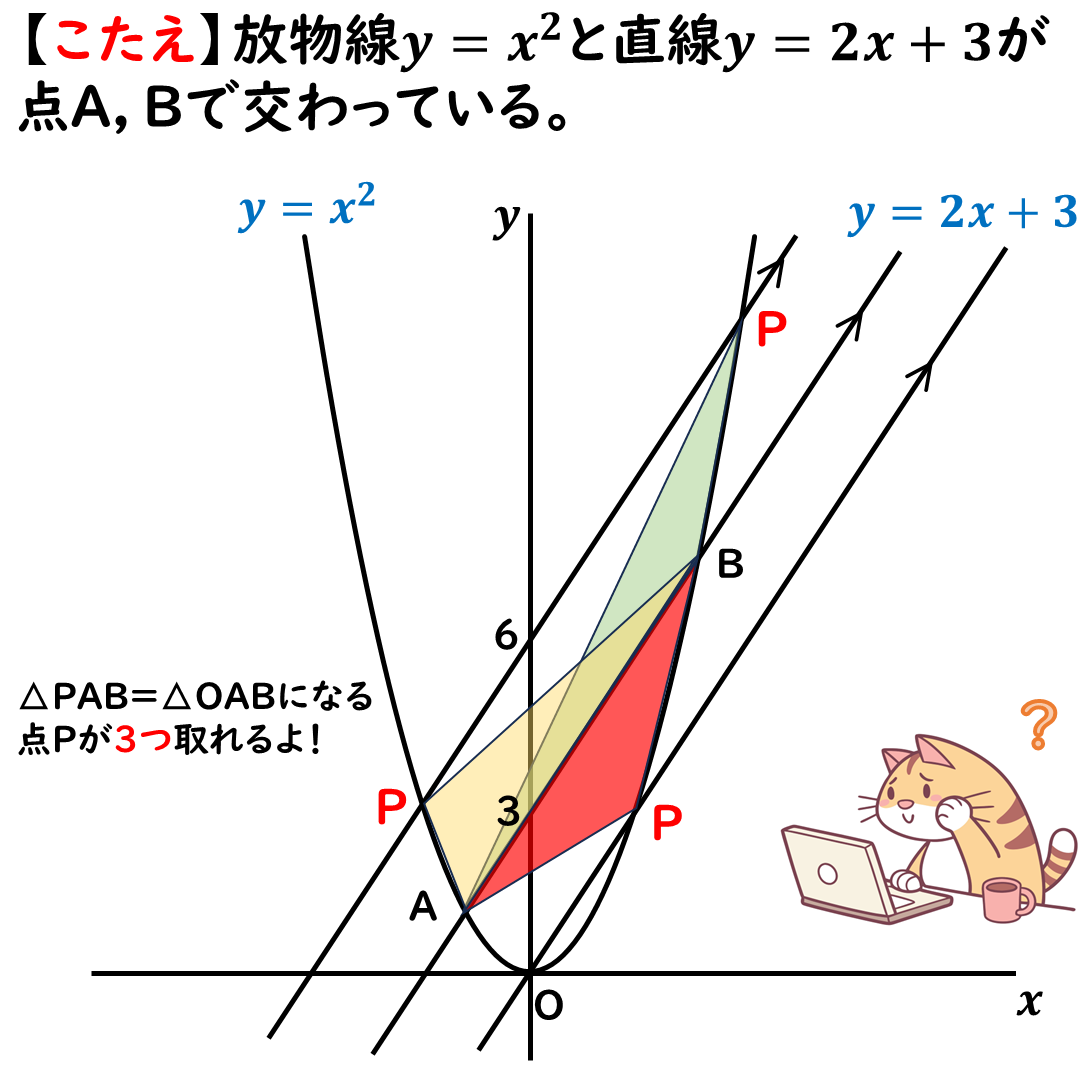

のんびり解説
さて,ここからは,
のんびりゆっくり。
少しずつ解説していきます。
そもそも,
この問題では等積変形を使っています。
中2数学の図形分野で
学習するのだけど,
お受験なしの
一般の公立中学校では,
応用レベルまで
学習することはありません。
\入試で出まくるのにおかしいYO☆/
等積変形とは

等積変形ってとても
おもしろいよね。
これが実力テストや入試レベルで
出まくる。
受験生ならば,良くも悪くも
そのことがわかるはずだ。
等積変形をくわしく学びたい
受験生!
まずはこちらをオススメします。
中2レベルで解けるよ。
まずは,△OABをチェックだ☆
今回の問題では,
等積変形はなさそうに
見えるけども。
補助線として平行線を書けば
等積変形が使えるの。
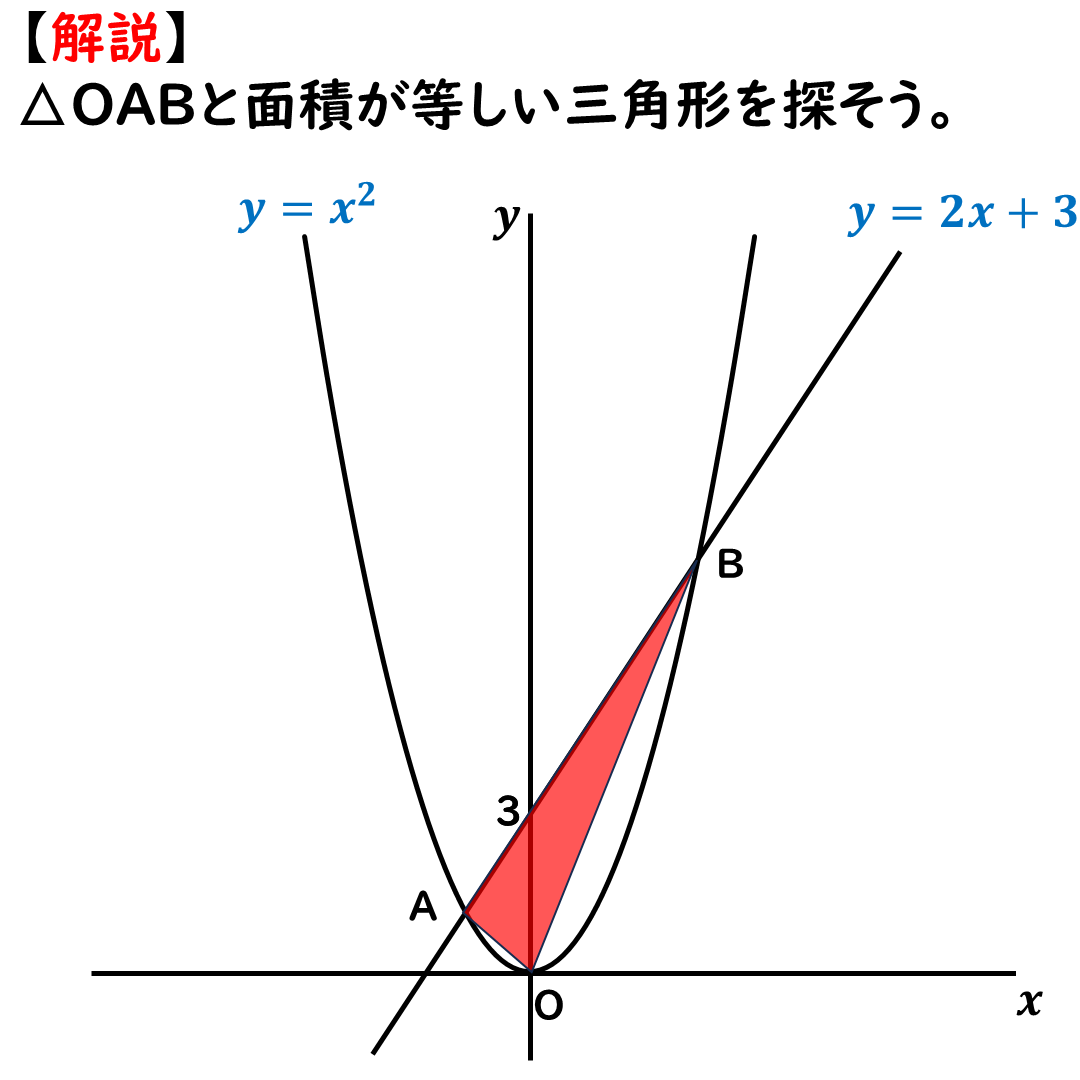
まずは,問題の△OABを
探しておこう。
この赤い三角形だ。
今回は面積を求める必要はない。
補助線の平行線をかこう
ほしい情報というのは,
△OABと面積が等しい三角形だ。
そのために,
y=2x+3のグラフに平行で
原点Oを通る直線,
y=2xのグラフをかくよ!
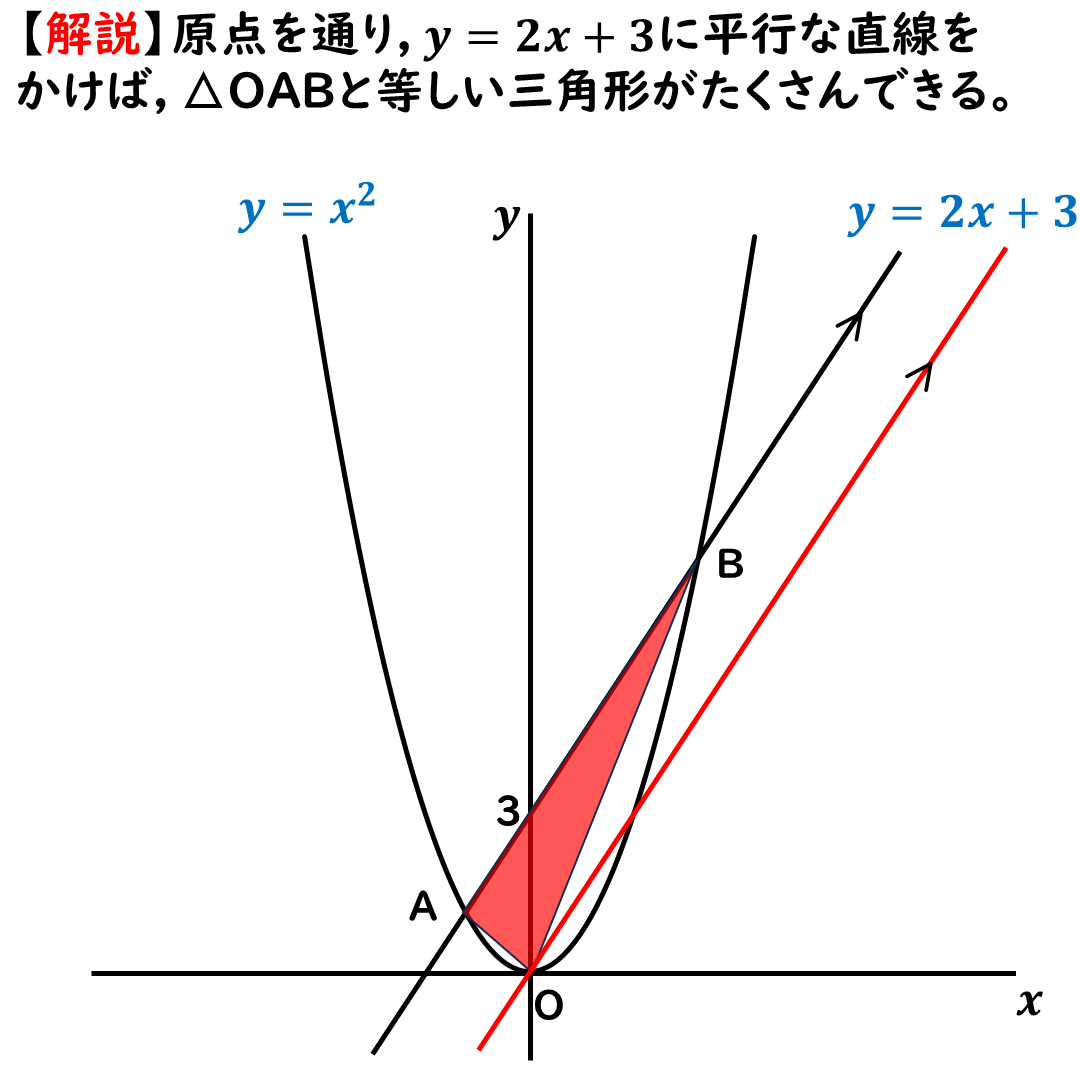
平行線をかいて,
点Oをずらしていくことで,
△OABと面積が等しい三角形が
たくさんできるよ!
こんな感じ。
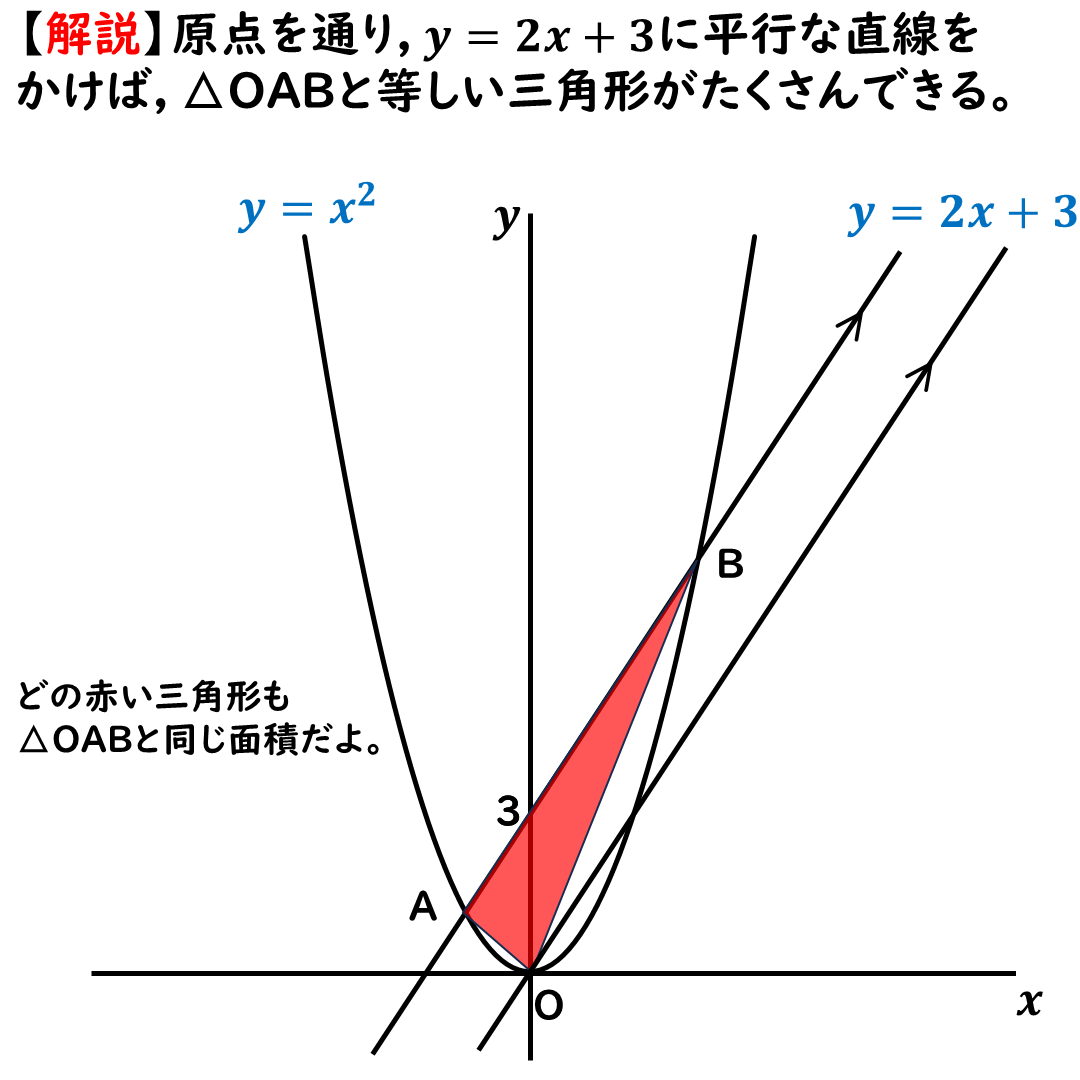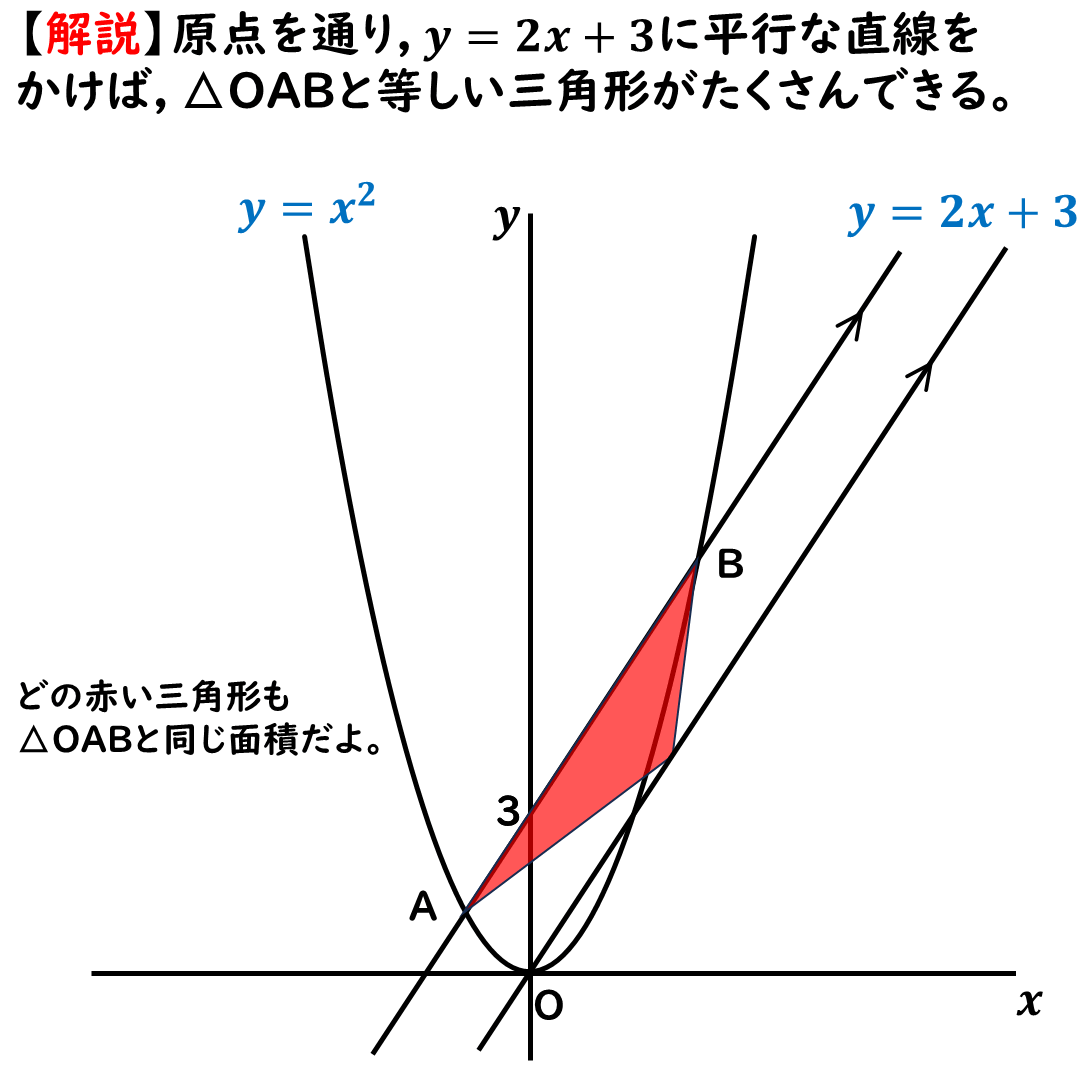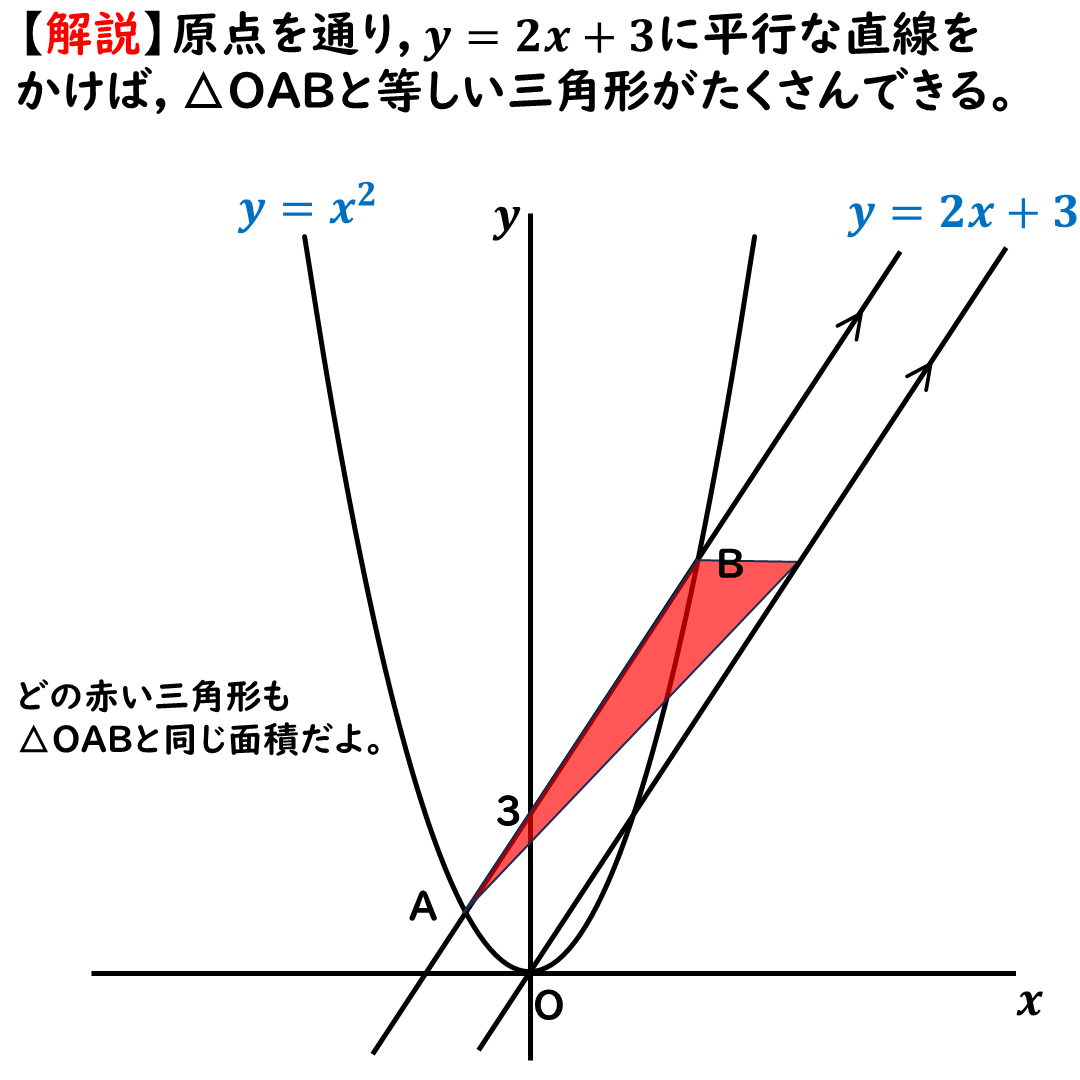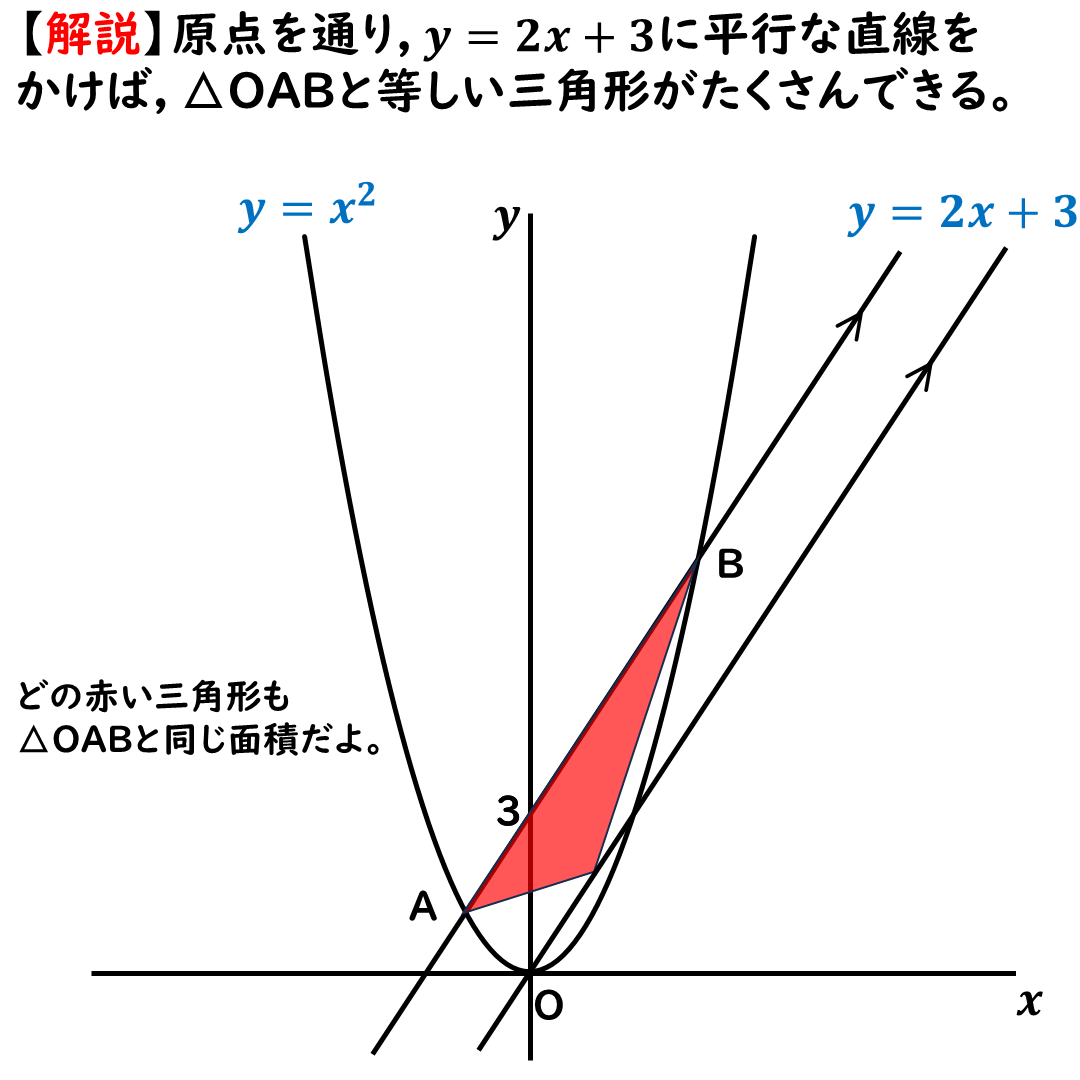
↑上記の画像では,
どの赤い三角形も
△OABと面積が同じになるよ。
底辺と高さが同じだからね。
問題の条件に合った点Pを選ぶ
たくさんできた△OABと
面積が等しい赤い三角形たち。
その中から,
問題の条件に合った三角形を
選び出そう。
その条件とは,
放物線上に点Pがある,
ということ。
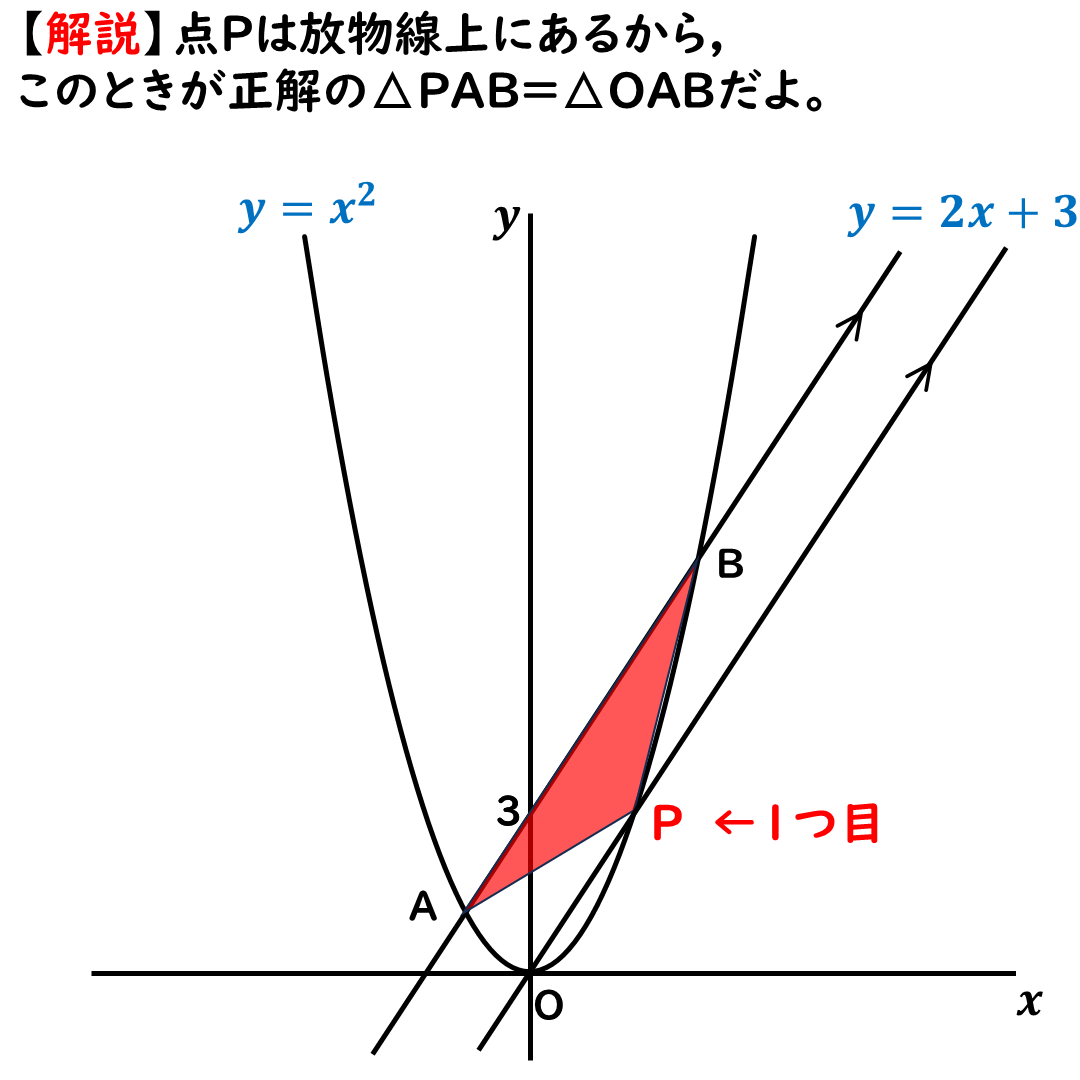
これが点Pの1つ目だよ☆
点Pの座標の求め方
点Pの場所はわかったけど
どうやって座標を求めるのか。
点Pは二次関数と
一次関数の交点だよ。
グラフの交点の座標は,
それぞれのグラフの式を
連立方程式にして解けば
求められる。
代入法が便利だよね。
今回は二次関数だから
2次方程式になるかなあ。
代入して,それぞれの式を
くっつける。
後は2次方程式の計算だね。

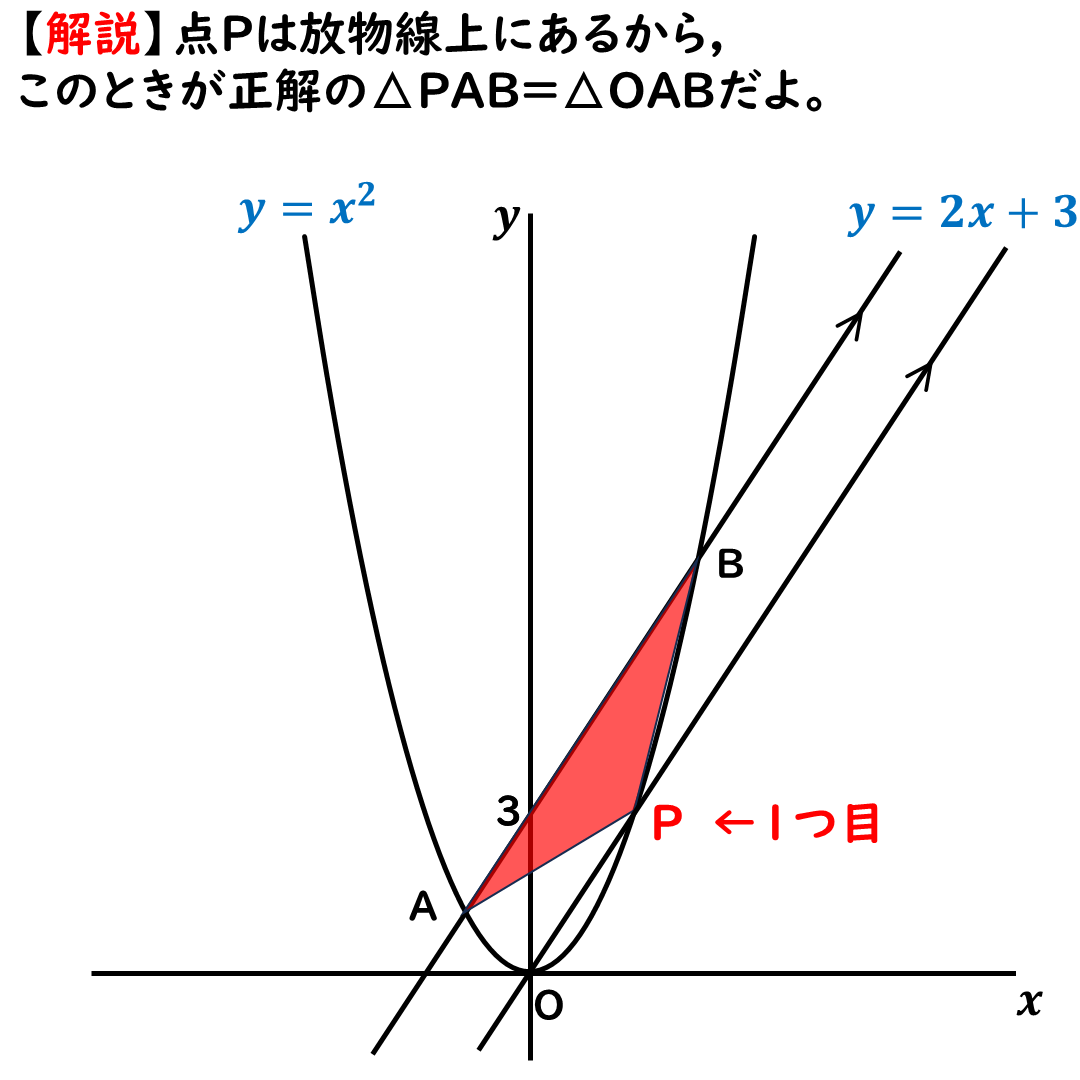
点Pはまだまだあるよ☆
点Pは1ヶ所だけではない。
全部で3ヶ所あるから,
残り2か所ある。
平行線は反対側の
上側にもひけるのだ。
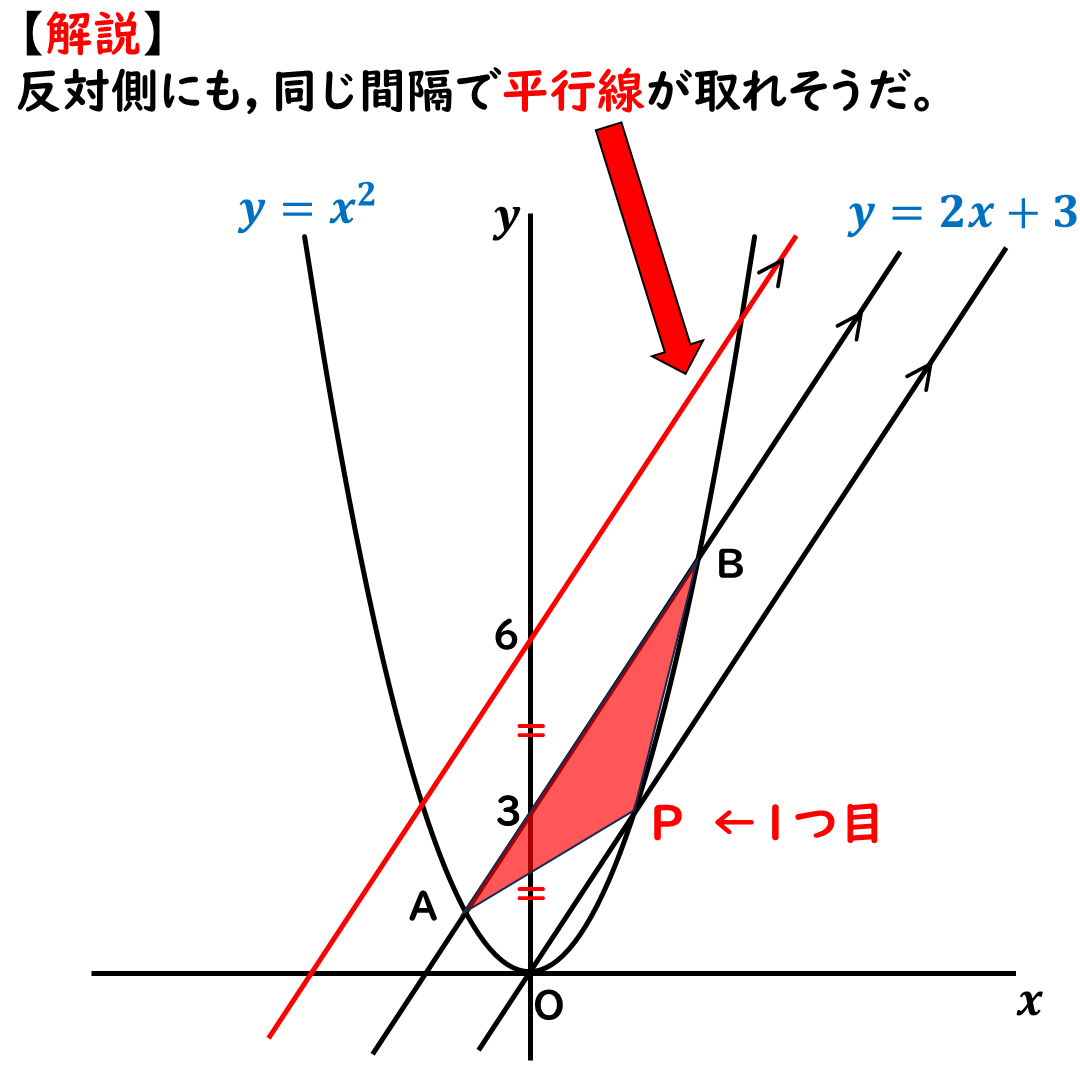
三角形の底辺は辺ABで
固定だから
高さもそろえよう。
そうすると,平行線として
y=2x+6のグラフが
考えられる。
y=2x+6のグラフなら
等間隔で
底辺も高さも一致。
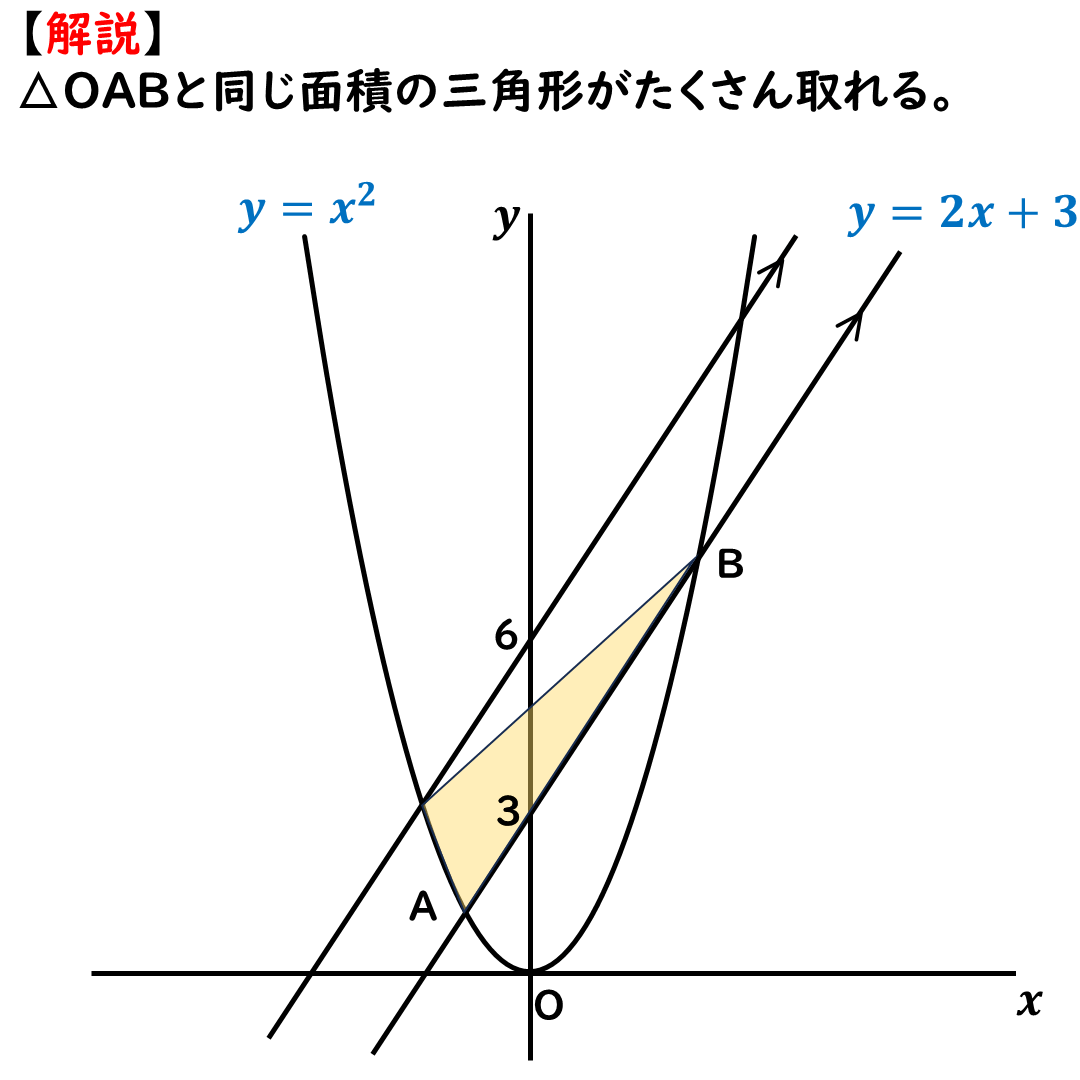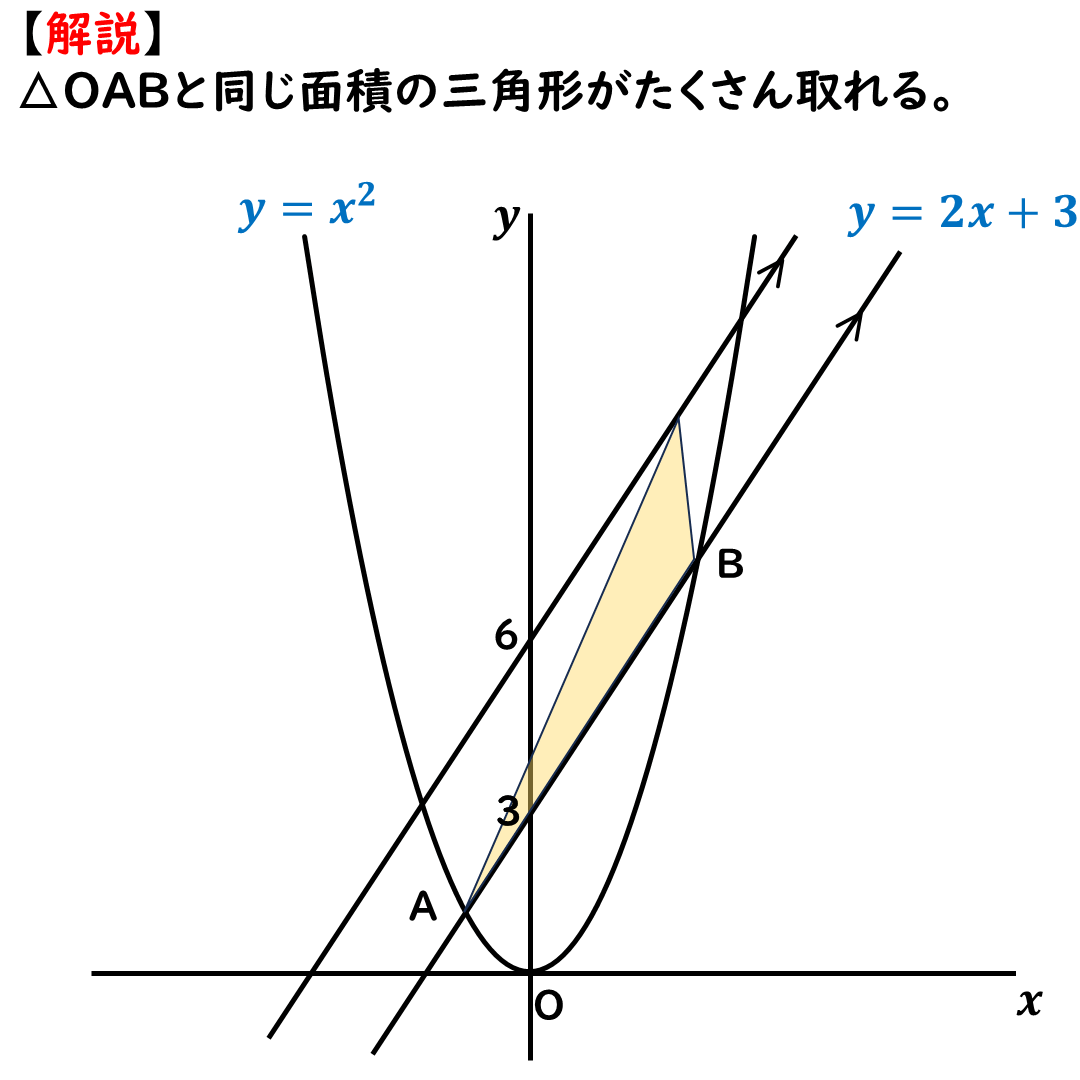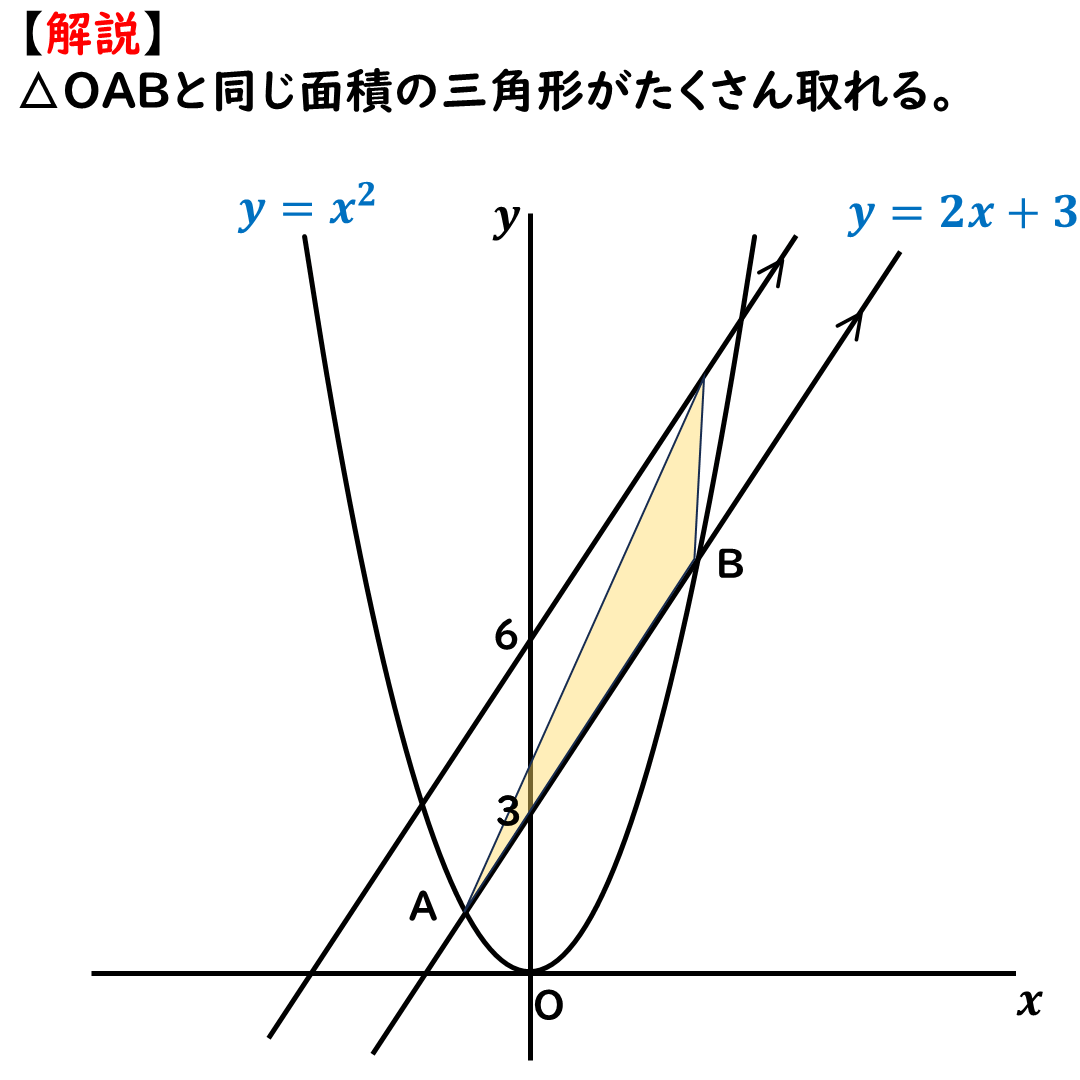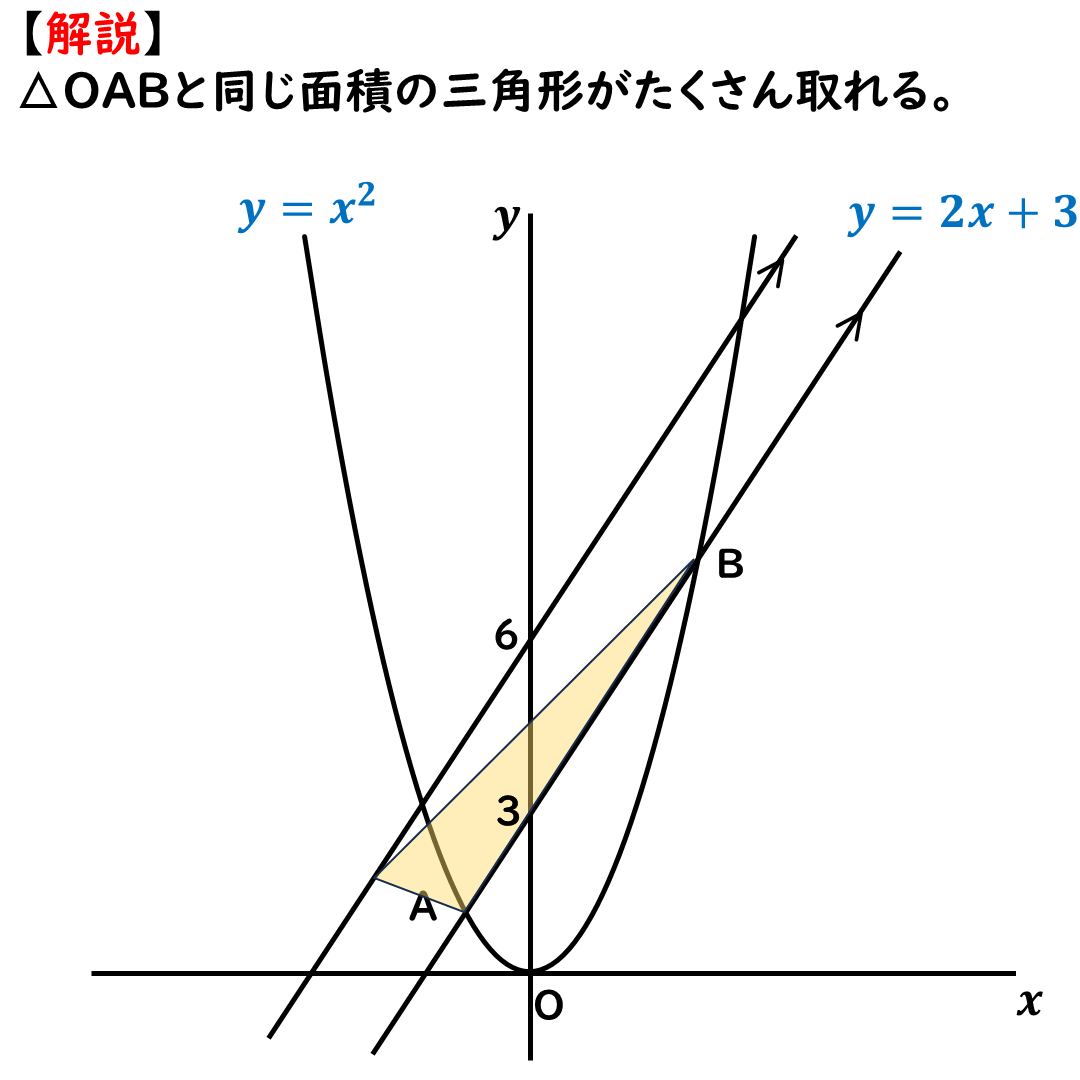
次の画像のように,
上側にも,
△OABと同じ面積の
三角形がたくさん取れるよ!
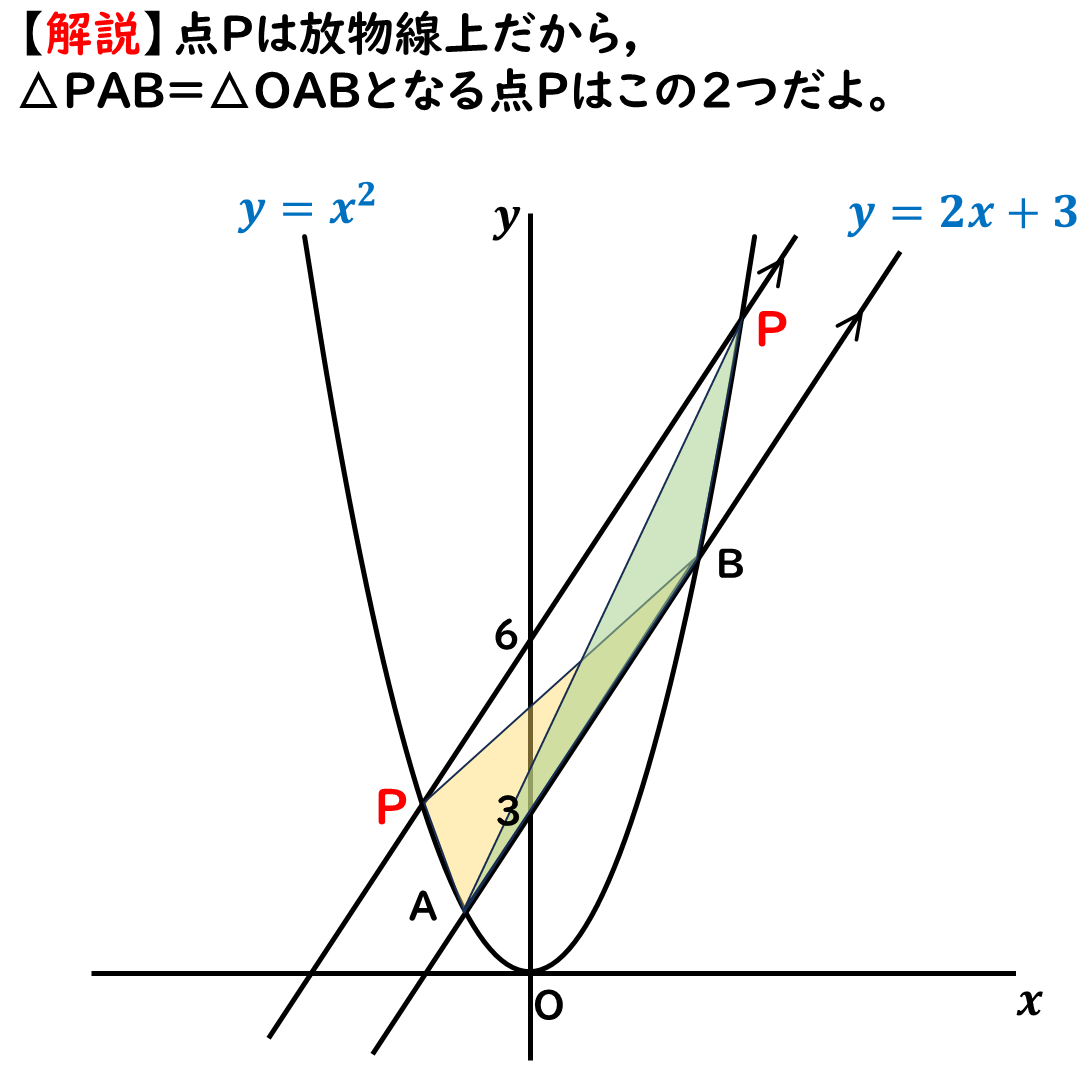
問題の条件としては,
放物線上に点Pがほしい。
だから,次の画像の位置になる。
この2ヶ所だ。
あとは,こちらも
グラフの式を連立させて
交点の座標を求めていこう。
二次関数が入っているので
二次方程式になる。
最終的に,
答えは全部で3ヶ所だ。

解の公式の計算等で注意!
たまーに計算をミスする
残念な生徒さんが
いらっしゃいます。
分数の約分についてです。
細かい計算を付けたので
ご参考まで。
以上,
二次関数の応用問題と
その解説でした!
他の問題も
ぜひチャレンジしてみてくださいね!
わからない問題があって
困っている生徒さん,保護者さま☆
私の授業をお申込みください。
一緒に解いて前に進もう☆
お待ちしています☆








コメントはこちらからどうぞ☆