応用！2次関数の面積

2次関数の応用問題にチャレンジ！

次の問題にチャレンジしてみてください。

2次関数と一次関数が混ざった，

よくある応用問題例です。

1問目は一次関数の式の問題

2問目は定番！△ＯＡＢの面積！

3問目は応用！動く点Ｐの問題です。

答えは下にあります。

解説動画もあります。

すぐ下にヒントがあるよ！

ヒント！

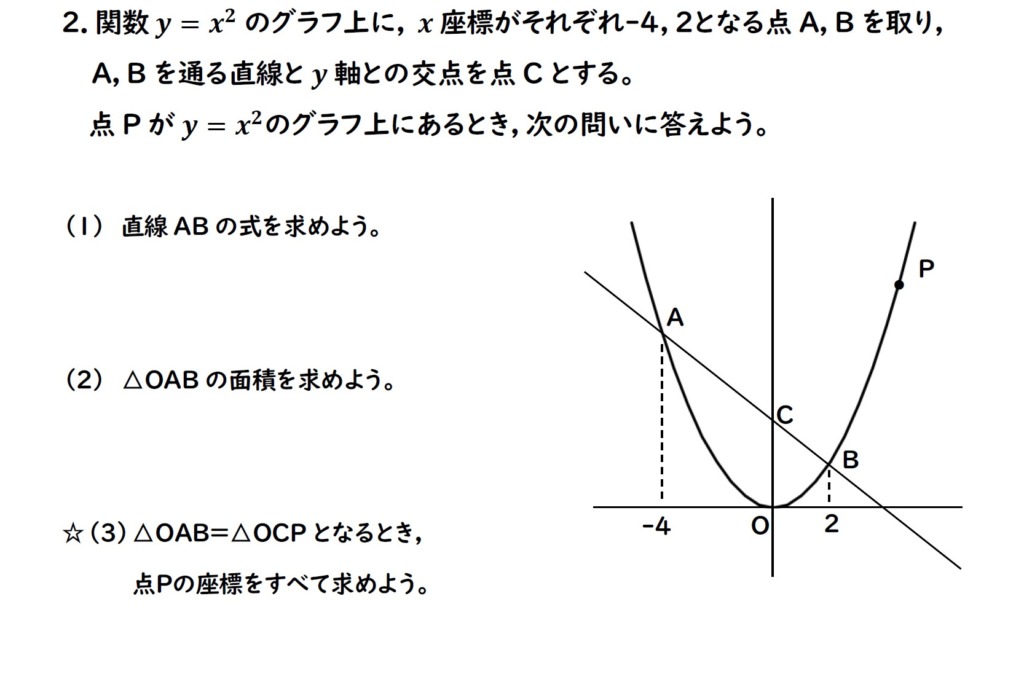
（１）

まずは点A，点Ｂの座標を求めよう。

次に，一次関数ｙ＝ax＋ｂですね。

上記の式にA(-4，16)，B(2，4)

を代入するとa,bの連立方程式になるよ！

もちろん，

変化の割合の考え方もアリですよ。

（２）

△ＯＡＢを左と右の三角形に分けて

考えるといいかも！

辺OCが底辺として使えます！

別解にて，

一発で求める方法載せています。

（３）応用です。

△ＯＣＰは，底辺として辺OCが

そのまま使えます。

次に，△ＯＣＰの高さは

点Ｐのｘ座標で決まります。

いくつにすれば

△OAB＝△OCPになるでしょうか

授業動画はこちら。

中3生と授業したときの録画です。

けっこうあっさり解いちゃってますが，

応用です。

答えと解説はこちら

こたえ

（１）　ｙ＝ー２ｘ＋８

（２）　２４

（３）（ー６，３６）,（６，３６）

正解できたでしょうか，

ココからは解説ページです。

（１）の解説です。

画像は変化の割合で解いています。

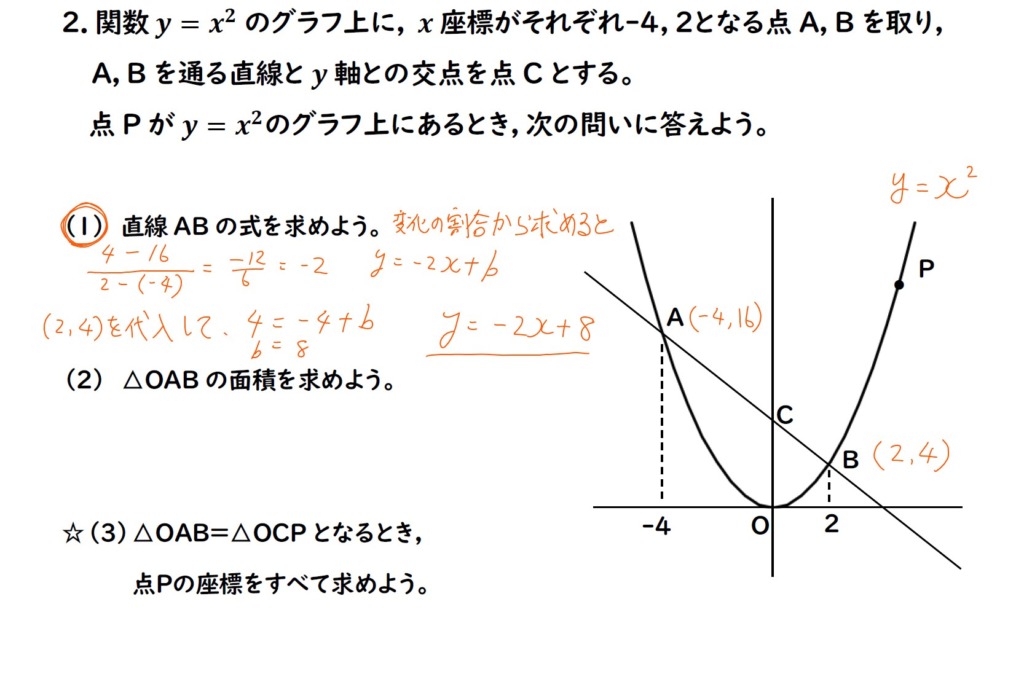
ｙ＝ax+bに代入する方法もあります。

その場合は，

(ー４，１６)を代入して

16=-4a+b・・・①

（２，４）を代入して

4=2a+b・・・②

①，②を連立方程式として

計算してみよう！

（２）の解説です。

ここでは，△OABを２つにわけて

解いています。

まず，△OABとは緑部分。

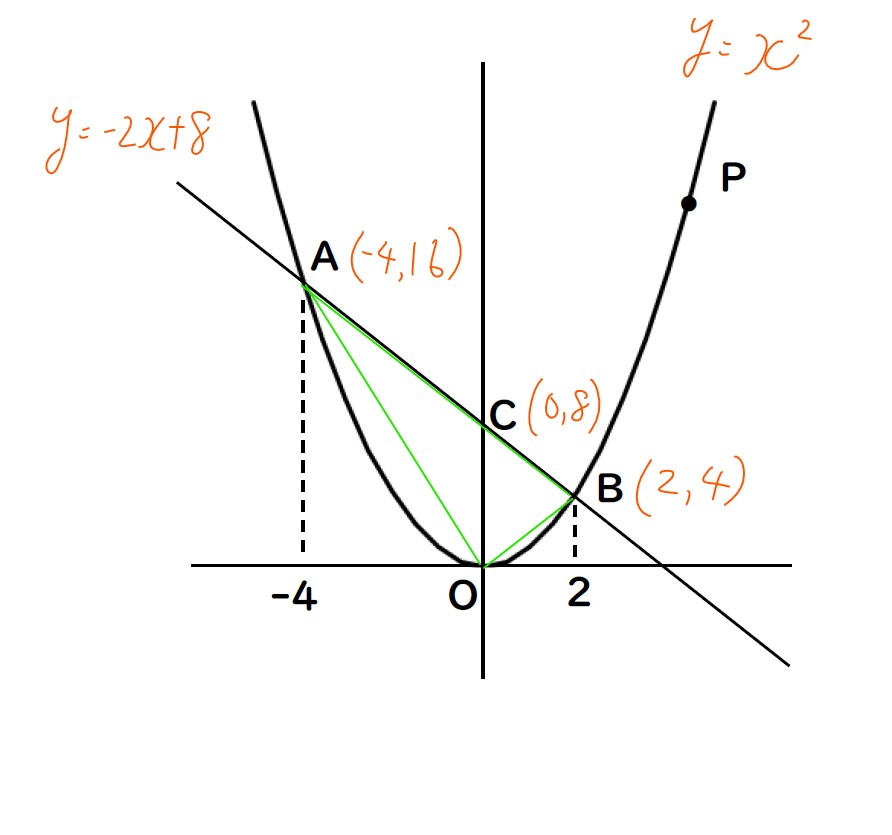
次に，△OABを①，②に分けます。

分け方は，ｙ軸で区切るといいかも！

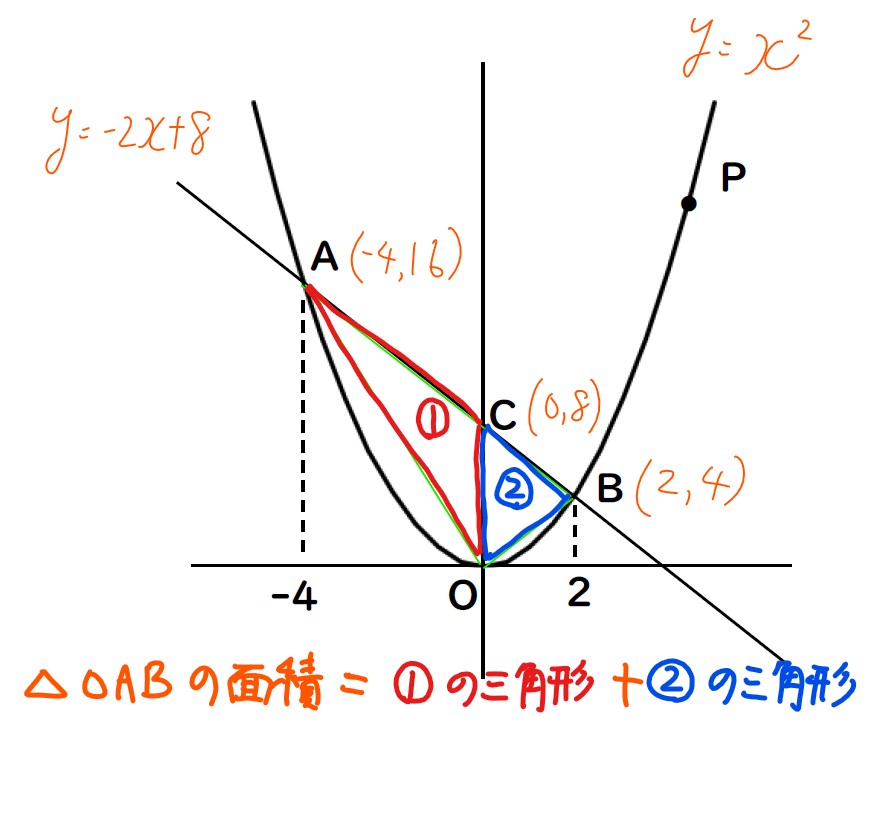
後は①，②の三角形の面積を

それぞれ計算するだけですが，

もうパニックの方が実はけっこう

たくさんいると思っています。

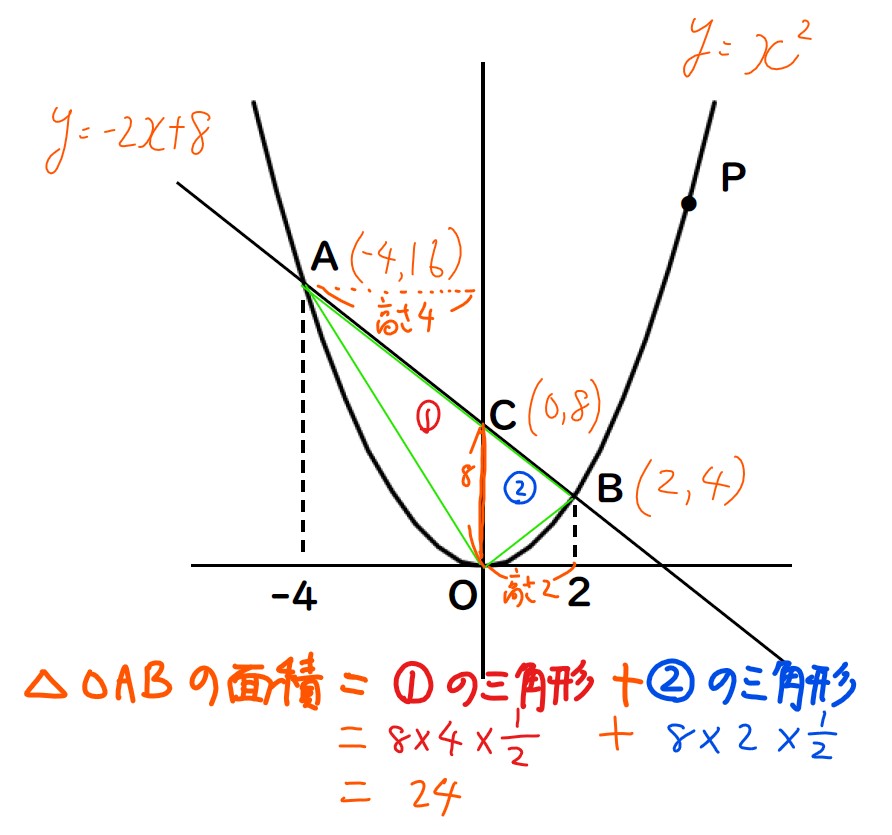
①の三角形の面積

底辺OC ×(高さは点Aのｘ座標) ÷２

＝８　×　４　÷　２

＝１６

点Aのｘ座標はマイナスじゃないか！

と思うかもしれませんが，

必要なのは絶対値。

マイナスであっても

４の距離があるよねという話。

②の三角形も

(底辺OC)×(点Bのｘ座標)÷２

＝８

①と合わせて24です。

最後に別解で

1発で求める方法を載せています。

ただし，応用なので無理せずに。

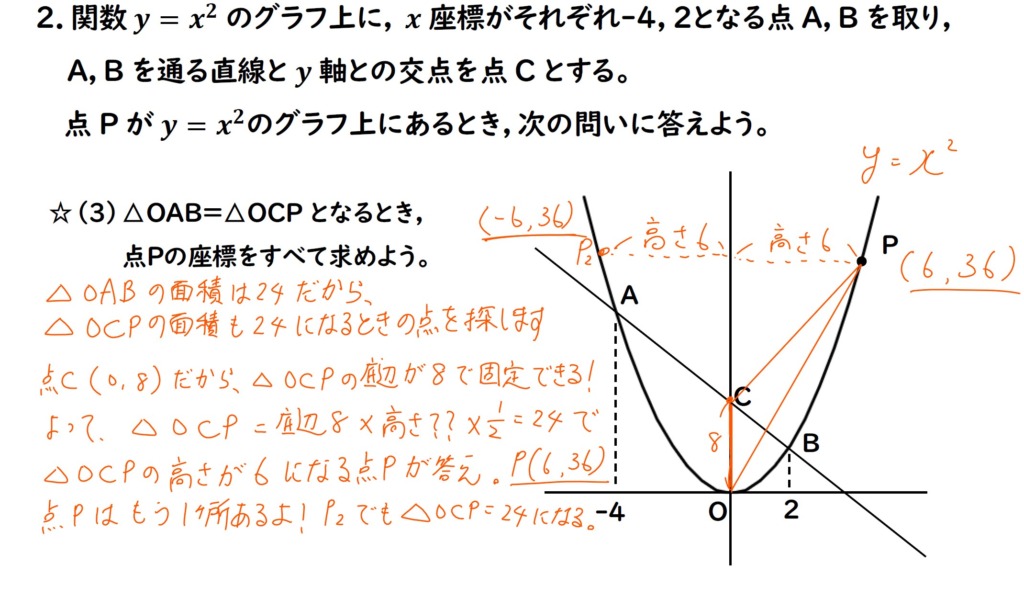
（３）は応用だけど実は簡単。

△OAB＝△OCP＝24

こうなる点Pを探します。

そもそも，△OCPの面積は

底辺OC ×(高さは点Ｐのｘ座標)÷２

で求められます。

つまり，

８ ×(点Pのｘ座標)÷２＝２４

点Pのx座標が6の距離であればOK。

そうなる点Pは次の2点。

（-6，36），（6，6）

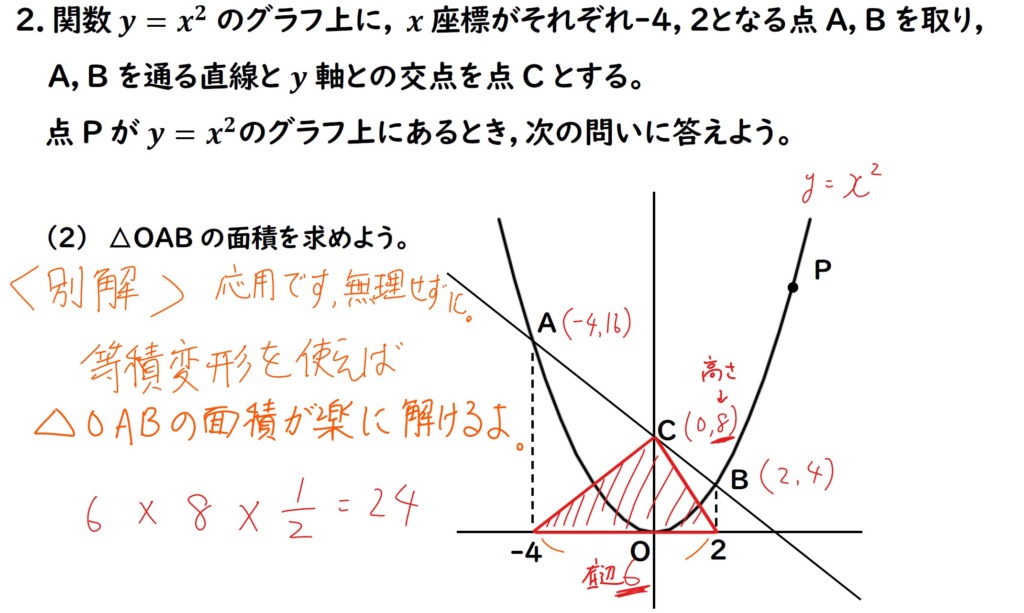
(応用)△ＯＡＢを簡単に求める

（２）の問題の△OABは，

次の図のように，

等積変形を使えば

簡単に求められます。

等積変形ってなに？？

解説の続きは？

という生徒さんは

気軽に質問してください！