オームの法則のグラフ問題４　電力・発熱量

グラフを効率よく使える問題にチャレンジ！

今回のオンライン授業動画はこちらです。

＜問題＞

2種類の電熱線ａ，ｂにそれぞれ電圧を加えて，流れた電流値を測定した。

次のグラフはその実験結果である。次の問いに答えなさい。

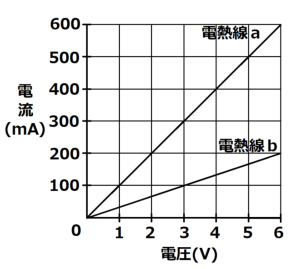
（１）　電熱線ａ，ｂを使って直列回路にした。回路全体の電流が200ｍＡのとき，回路全体の電圧を求めなさい。

（２）　電熱線ａ，ｂを使って並列回路にした。電源電圧３Ｖのとき，回路全体の電流値は何Ａか。

（３）　電熱線ａに300ｍＡの電流を5分間流した。このときの発熱量は何Ｊか。

（４）　電熱線ａ，ｂにそれぞれ６Ⅴの電圧を加えて，10分間電流を流した。電熱線ａの発熱量(Ｊ)は，電熱線ｂの何倍か。

解答解説はこちら！

（１）　８Ｖ

電熱線ａ，ｂの抵抗を求めていくやり方もあるけど，グラフを使うと楽に求められます。

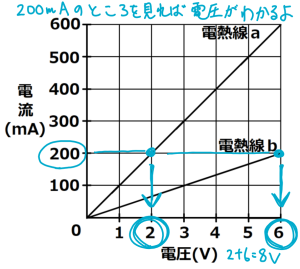
直列回路では電流がどこも等しいので，200ｍＡのところを見れば，加わる電圧値もわかるようになっています。

答えは，２＋６＝８Ｖ

（２）　0.4ｍＡ

電熱線ａ，ｂの抵抗を求めていくやり方もあるけど，グラフを使うと楽に求められます。

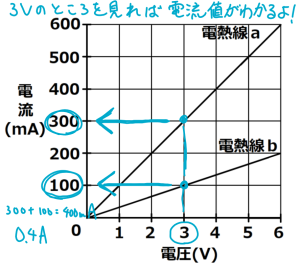
並列回路では電圧は電源に等しいので，3Ⅴのところを見れば，流れる電流値もわかるようになっています。

答えは，300＋100＝400ｍＡ＝0.4Ａです。

（３）　270Ｊ

電熱線ａに300ｍＡの電流が流れているとき，グラフから３Ｖの電圧が加わることがわかりますね。

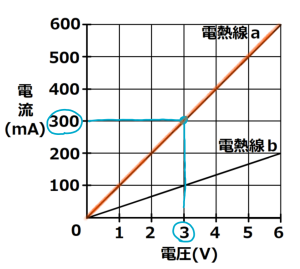
発熱量(Ｊ)＝電力×時間(秒)で求められます。よって

0.3Ａ×3Ｖ×5分×60＝270Ｊ

（４）　3倍

単純に，流れる電流だけ3倍になっているから3倍！でもＯＫです。

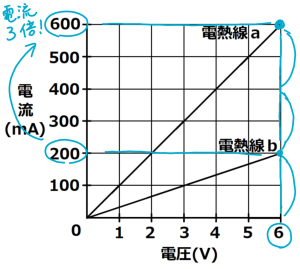
ちゃんと計算すると，

発熱量(Ｊ)＝電力×時間(秒)により，

電熱線ａの発熱量(Ｊ) ＝ 0.6Ａ × 6Ｖ × 10分 × 60

　　　　　　　　　　 ＝2160Ｊ

電熱線ｂの発熱量(Ｊ) ＝ 0.2Ａ × 6Ｖ × 10分 × 60

　　　　　　　　　　 ＝720Ｊ

ここからも，電熱線ａの発熱量は，電熱線ｂの発熱量の3倍だとわかりますね。

生徒さんと一緒に進めています。

オンライン授業動画もぜひ視聴してみてください。

おすすめ記事:

オームの法則のグラフ問題３　電力・発熱量 電気用図記号を覚えよう！ 並列回路の電流と電圧を求めよう！２ 直列回路の電流と電圧を求めよう！３ オームの法則のグラフ問題１ 回路全体の電圧を求めよう！