
高校受験の数学では,
2次関数の応用問題が必ず出ます。
特に,グラフや軸にできる三角形の
面積を求める問題が出やすいです。
そこで今回,
問題を制作して授業をしました。
そのときの記録を公開いたします。
あなたもぜひ
問題にチャレンジしてみてください☆
難易度★★ 2次関数の応用問題
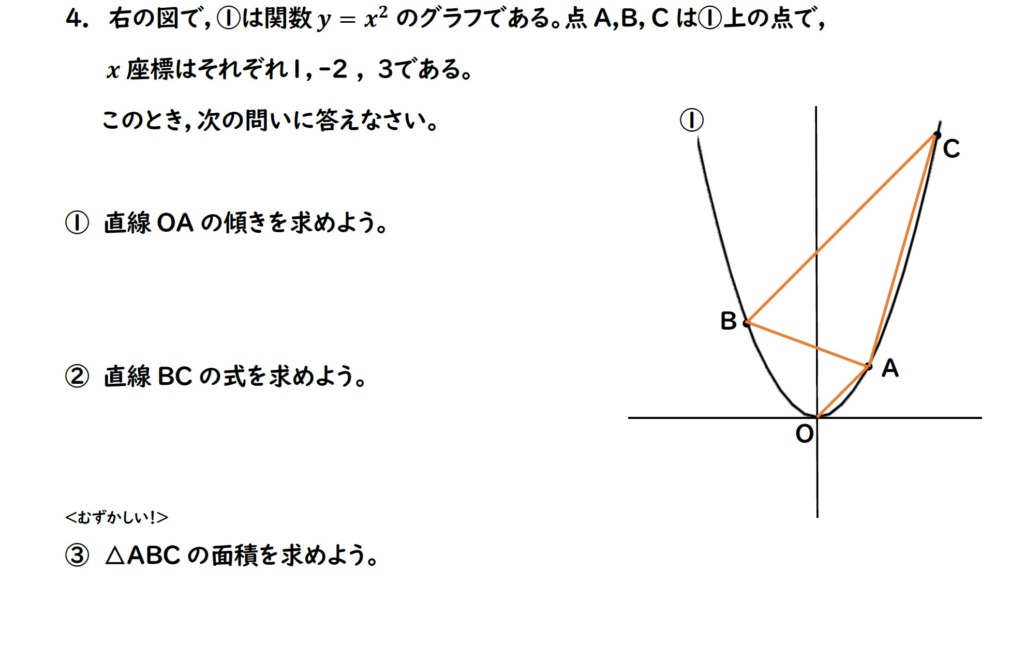
次の問題にチャレンジしてみてください。
①~③まであります。
最後の③が難しめです。
でも,気付けば1分で解けるかも!
答えや解説は下にあります。
解説動画もありますので,
一緒に学んできましょう!
実際の授業で学ぼう!
中3生と授業したときの録画です。
あなたもぜひご一緒に!
動画では,悩みに悩んだ生徒さんが,
解き方に気付いて。
そこからは
あっという間に解いてしまいました。
こたえと解説
① 傾き 1
② 直線BCの式 y=x+6
③ △ABCの面積 15
①の解説
原点(0,0)とA(1,1)を
通る直線の傾きを求めます。
y=axに代入すればOK!
傾きは1です。
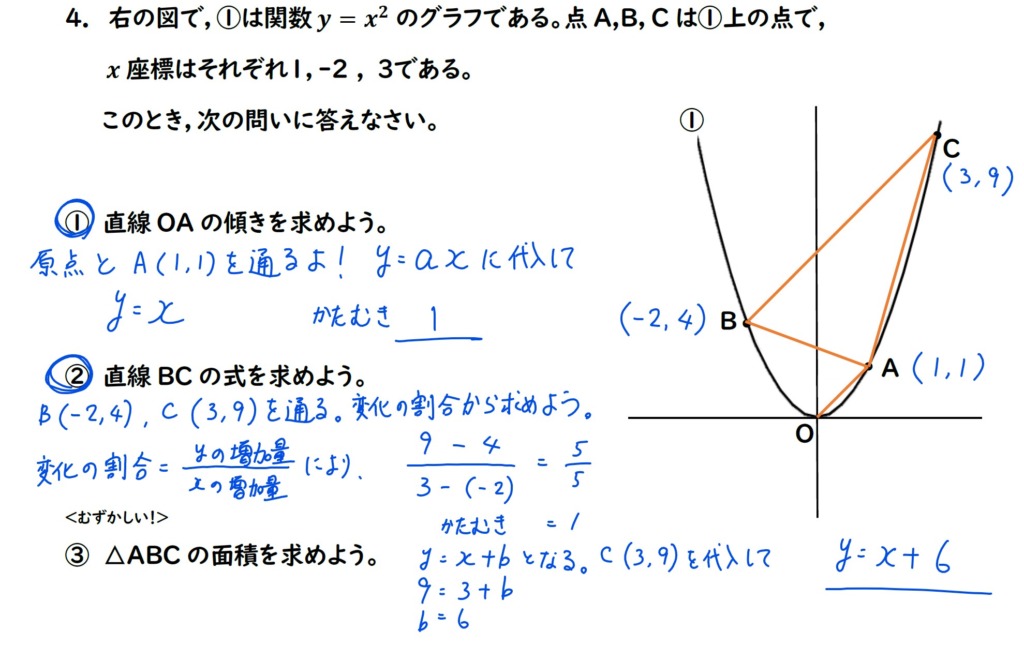
②の解説
B(ー2,4),C(3,9)を
通る直線の式を求めます。
下の画像のように,
変化の割合の式を求めてもいいですが,
ここでは連立方程式で解説してみます。
y=ax+b の式にB(-2,4)を
代入して,
4=-2a+b・・・ア
y=ax+b の式にC(3,9)を
代入して,
9=3a+b・・・イ
アとイの連立方程式を解くことで,
y=x+6 が出ます。
③の解説 難しめ★★
気付けば1分!
△ABCの面積を求めますが,その際に
気付いてほしいことががあります。
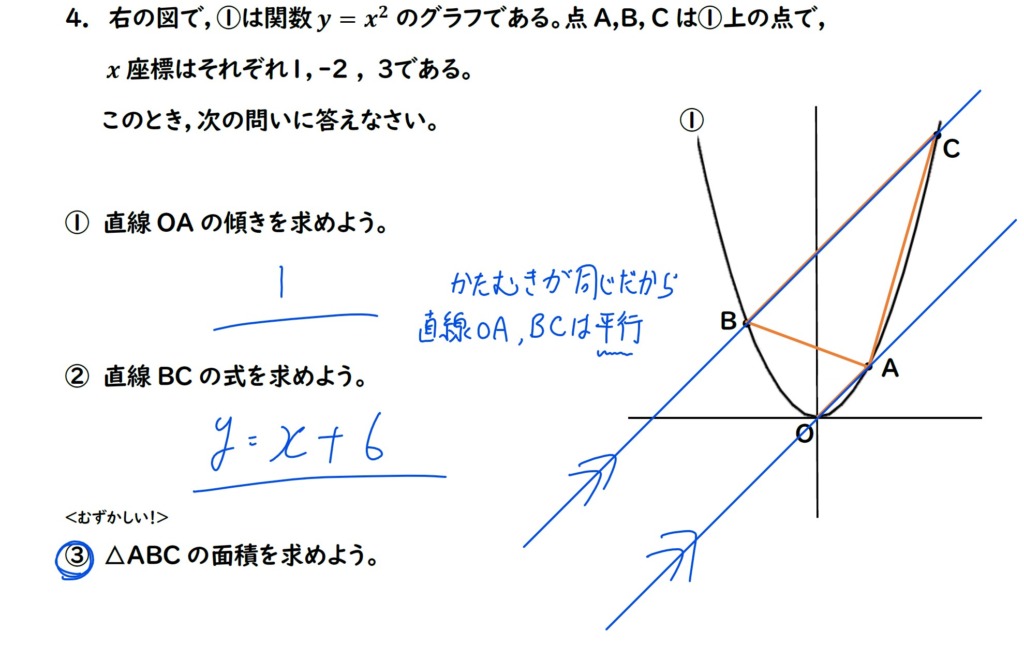
①,②で求めた,
①直線OAと②直線BCは
傾きが同じだから平行だよ!
実は,入試含めた実力テストというのは,
まず①を解いて,次に②を解いて,
それらを使って③を解くと効率がいい☆
という仕組みが多いです。
もちろん例外はありますが,
けっこう使えるテクニックです。
さて,
①,②をヒントにするわけですが,
どう使うか,ですよね。
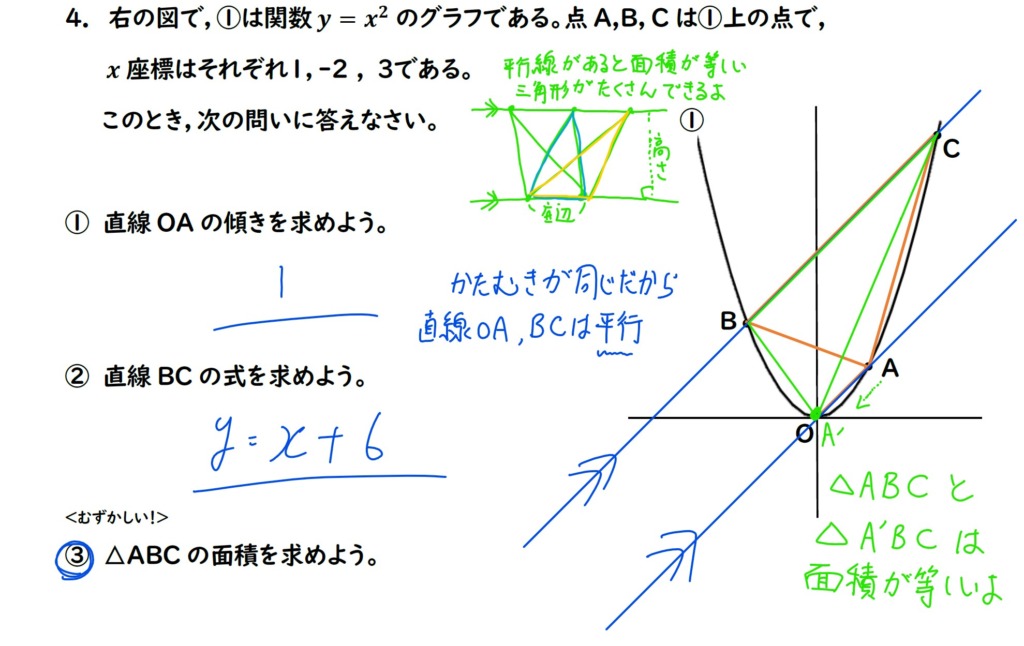
実は,平行線にできる三角形は,
底辺をそろえてしまえば
面積そのままに変形が可能です!
等積変形(とうせきへんけい)といいます。
今回は,
△ABCは,辺BCを底辺として,
点Aを,原点Oまで移動します。
これを点A’とします。
そこでできる
△A’B Cと△A B Cの面積は
同じ面積なのです。
平行線って便利!
点Aが原点まで移動したことで
面積を求めやすくなりました。
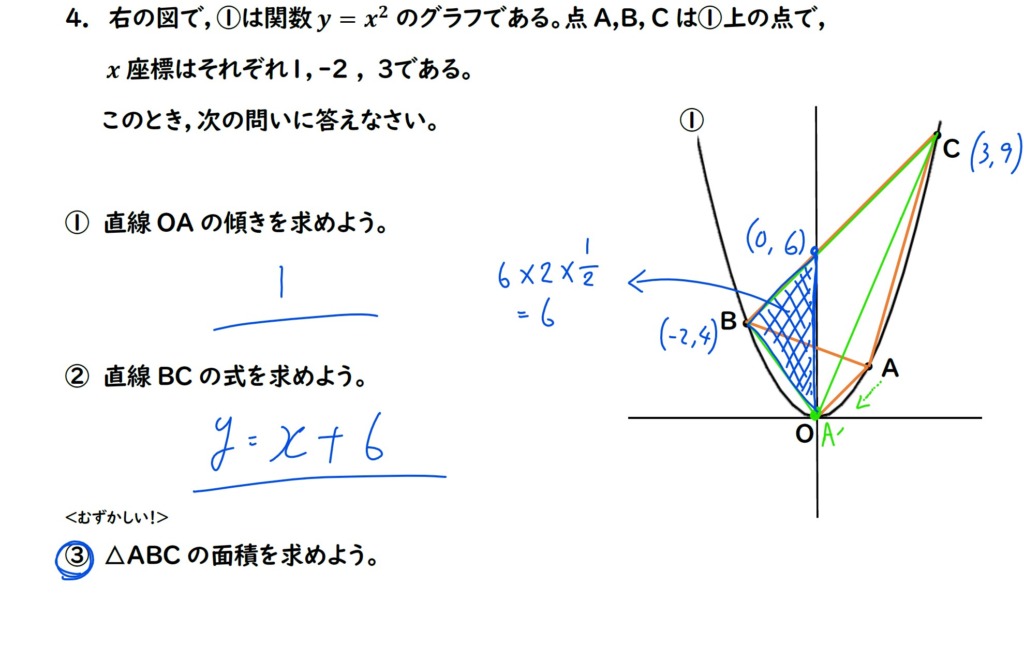
下の図のように,
y軸で左と右の三角形にわけます。
左の三角形は,
底辺6,
高さは点Bのx座標の絶対値の2を
使って,6×2÷2=6
次に,右側の三角形の面積も
求めます。
底辺は6,
高さは点Cのx座標の3を使って
6×3÷2=9
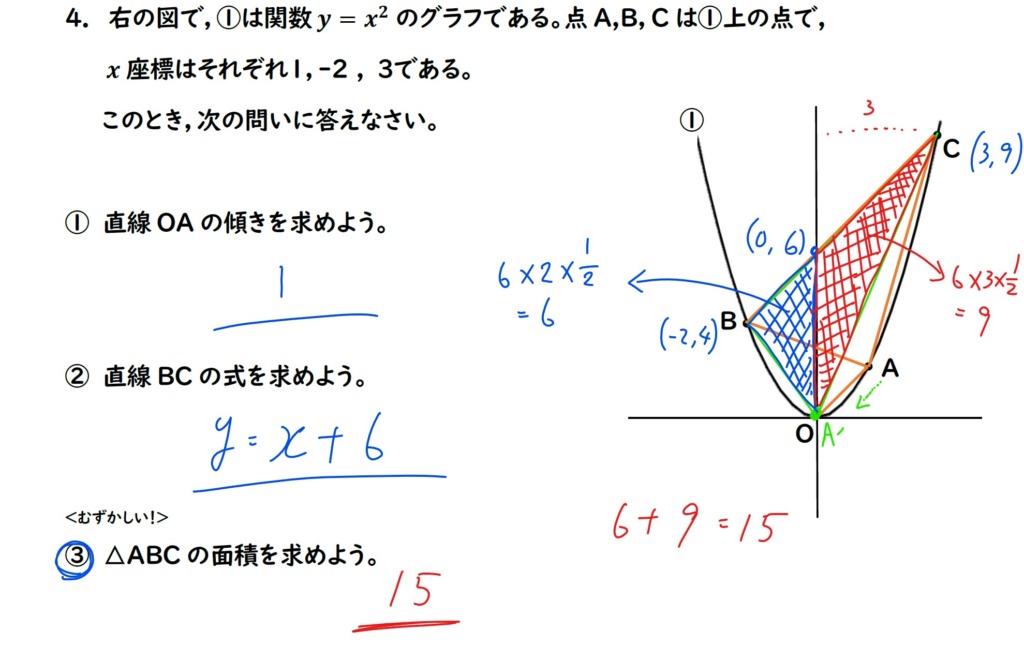
下の図で,
左の青い三角形が6,
右の赤い三角形が9ですから
△ABCの面積は15です。
今回の問題&解説は以上です。
他の分野もぜひご覧くださいね。






