単発の解説授業はじめました！
一次関数 直線で囲まれた面積を求めよう！ 後編
直線で囲まれた部分の面積を求めてみよう！
オンライン個別授業動画です，ぜひ視聴してみてください。
今回は後編になります。
前編はこちら。
＜ 問題 ＞
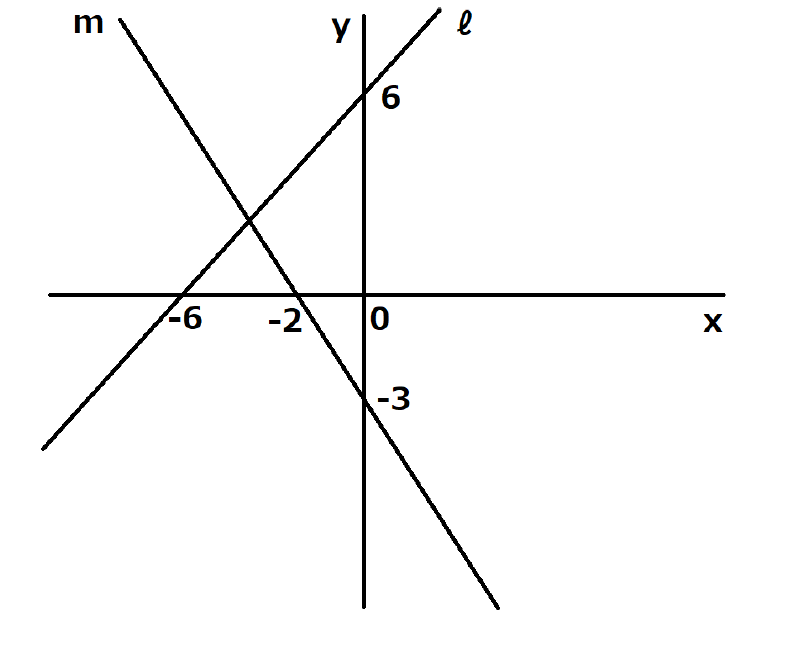
次の図で，直線ｍ，直線ℓ，ｙ軸に囲まれた部分の面積を求めなさい。
座標の1メモリを1㎝とする。
正解はこちら！
前編の動画で，直線ｍと直線ℓの式と，2直線の交点の座標は求めていますので，続きからです。
求めたい部分の面積はこちらです。三角形ですね。
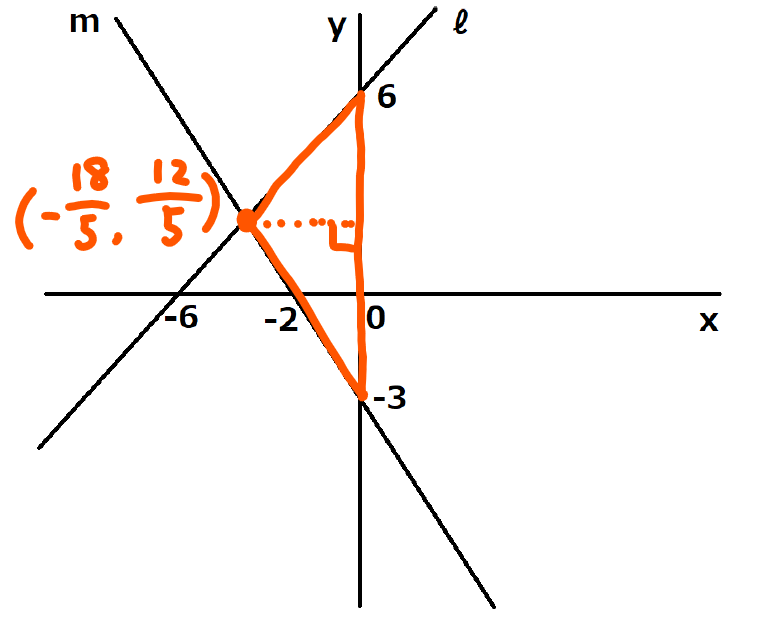
三角形の面積は，底辺×高さ÷２で求められます。
底辺はy軸から求められます。６＋３で９ですね。３は絶対値を使います。
高さですが，直線ｍと直線ℓの交点のｘ座標を使います。絶対値を取って\(\displaystyle \frac{18}{5}\) です。
ですので，
三角形の面積＝\(\displaystyle 9×\frac{18}{5}×\frac{1}{2}=\frac{81}{5}\)
こたえ \(\displaystyle \frac{81}{5}cm^2\) になります。
