一次関数の利用で出てくる,
動点Pの問題です。
これ,嫌いな人が多いんじゃないかと。
実力テストとかでもよく出るし。
今回は,例題を出して解説してみます。
画像を動かして視覚的に学べるよ☆
それでは,はじまりーはじまり~
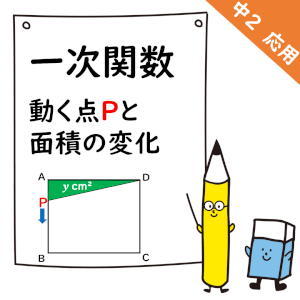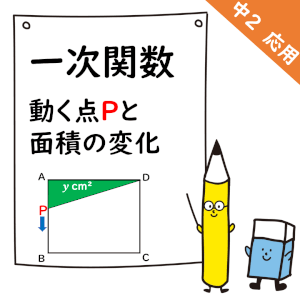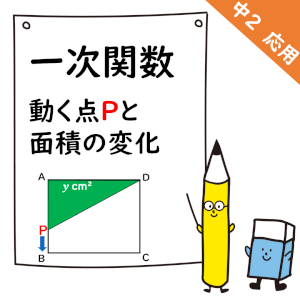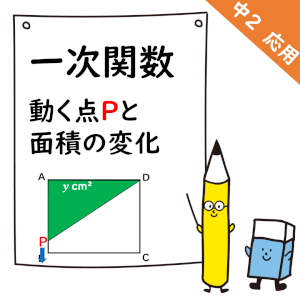
動く点Pと面積変化の問題
次の問題にチャレンジしてみようね。
答えは下に用意してあるよ!
まずは考えて見てね。
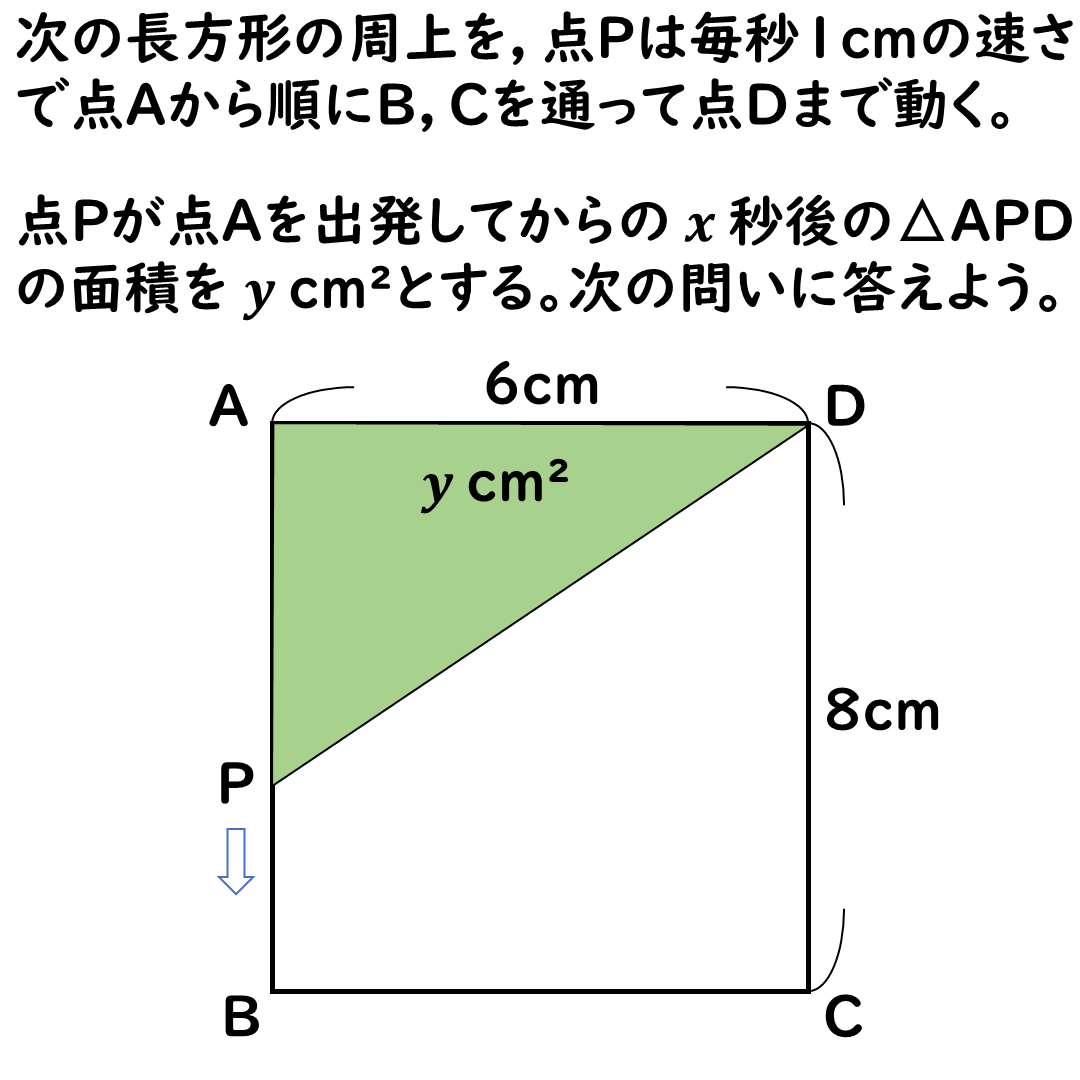

【ヒント】点Pは何cm動くのか。
この問題って,
点Pが動くんだけども。
問題には,
画像が1枚あるだけだから,
あとは頭のイメージで解く必要が
あります。
ムズカシー!
そこで,まずは
点Pってどう動くのか。
動く画像にしてみたよ。
こんな感じ。
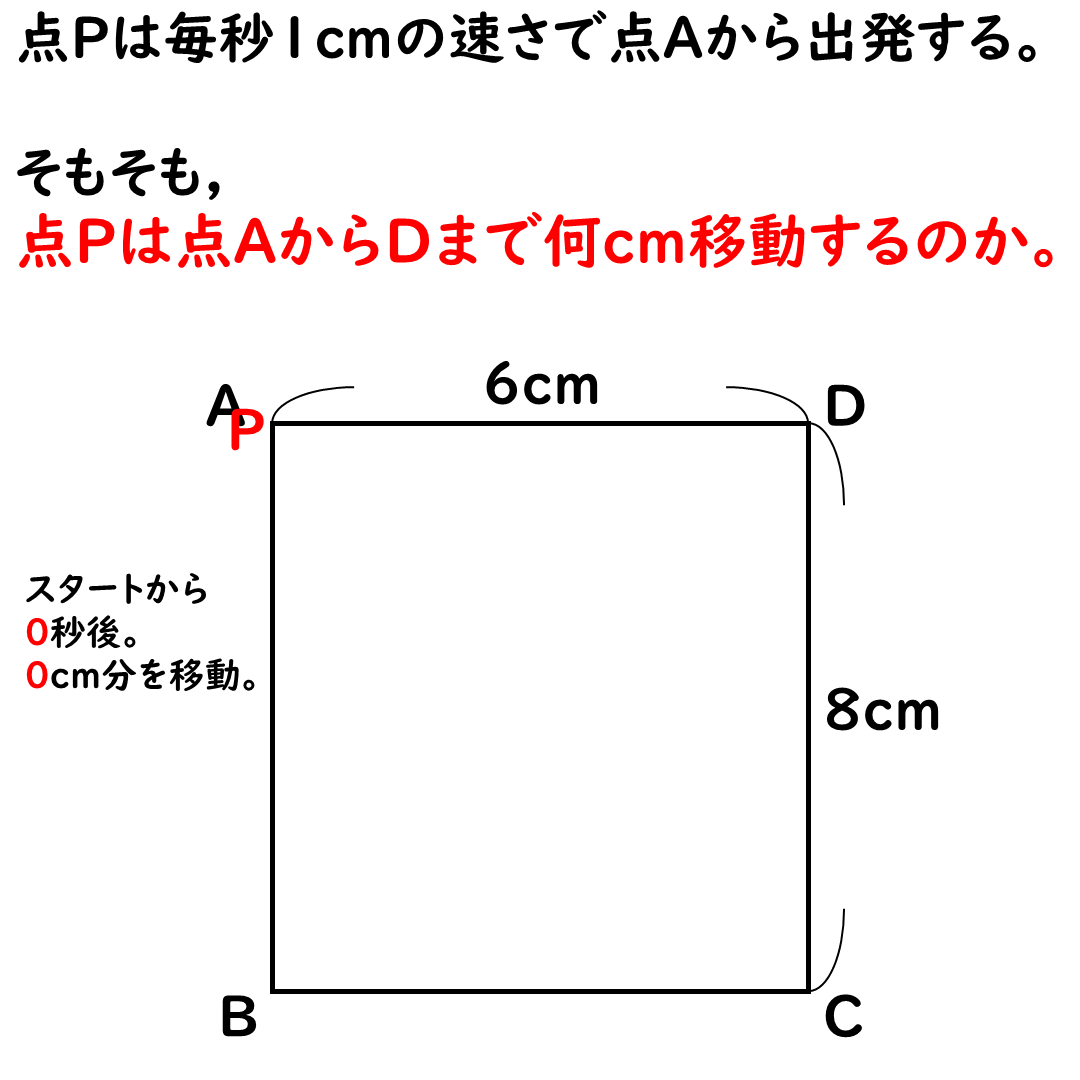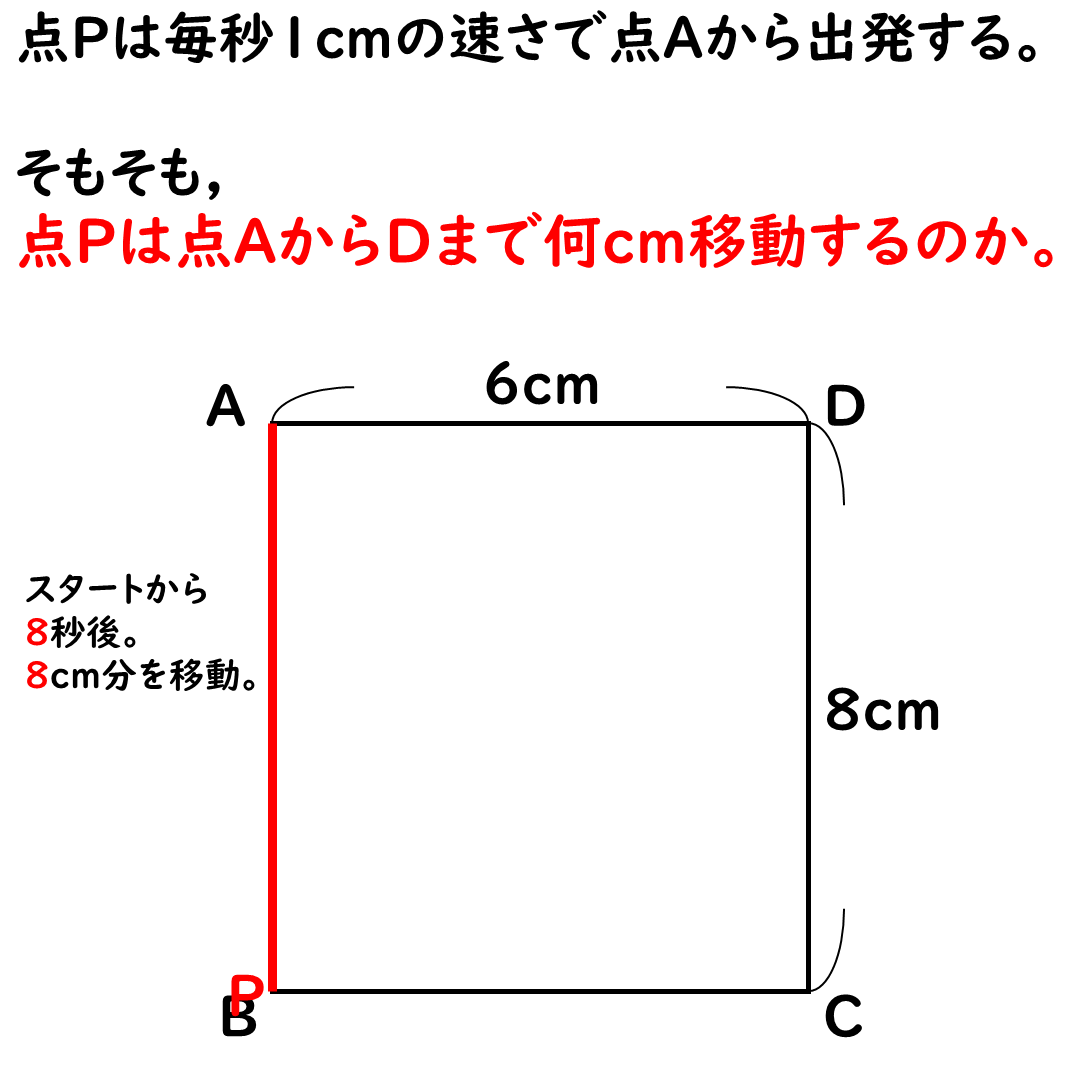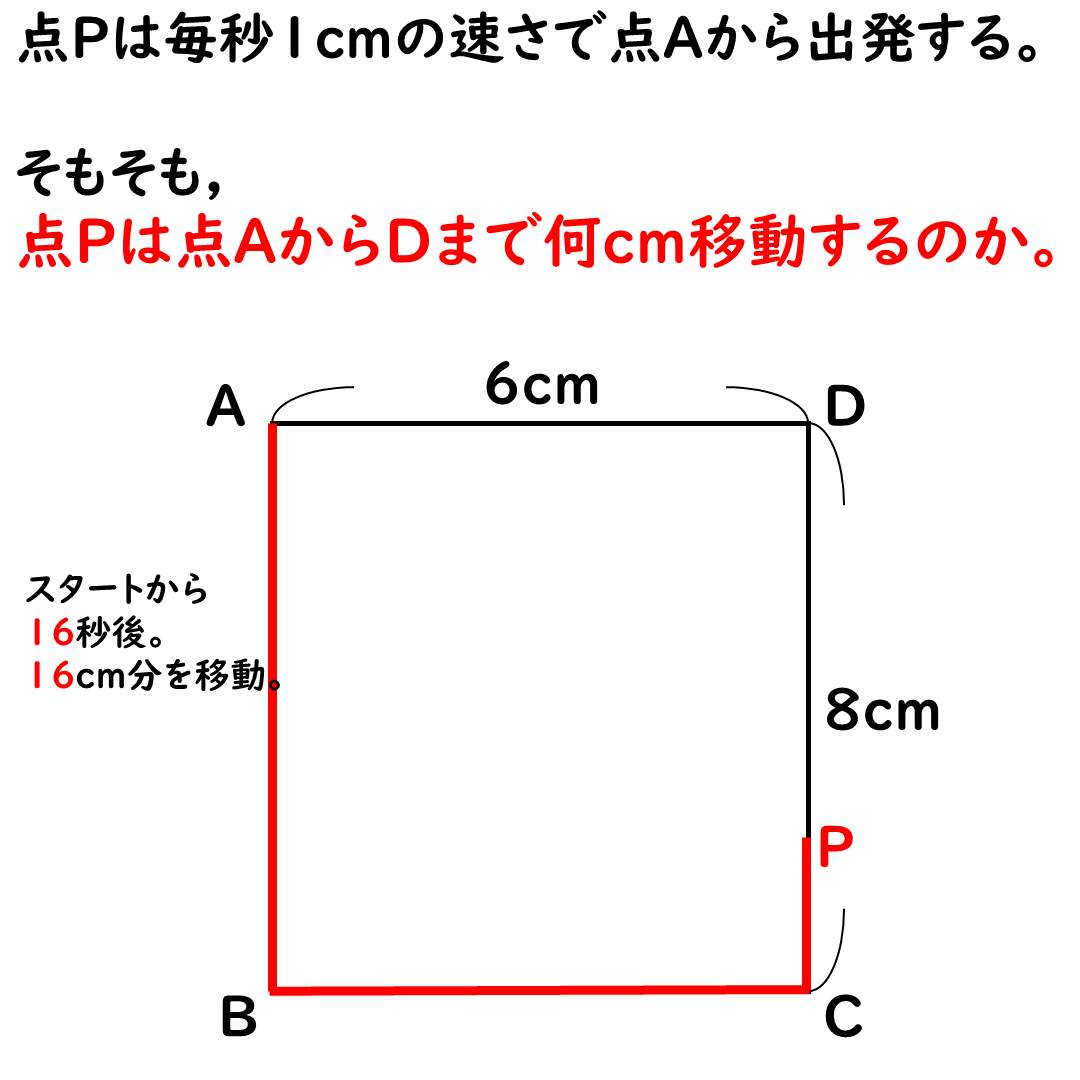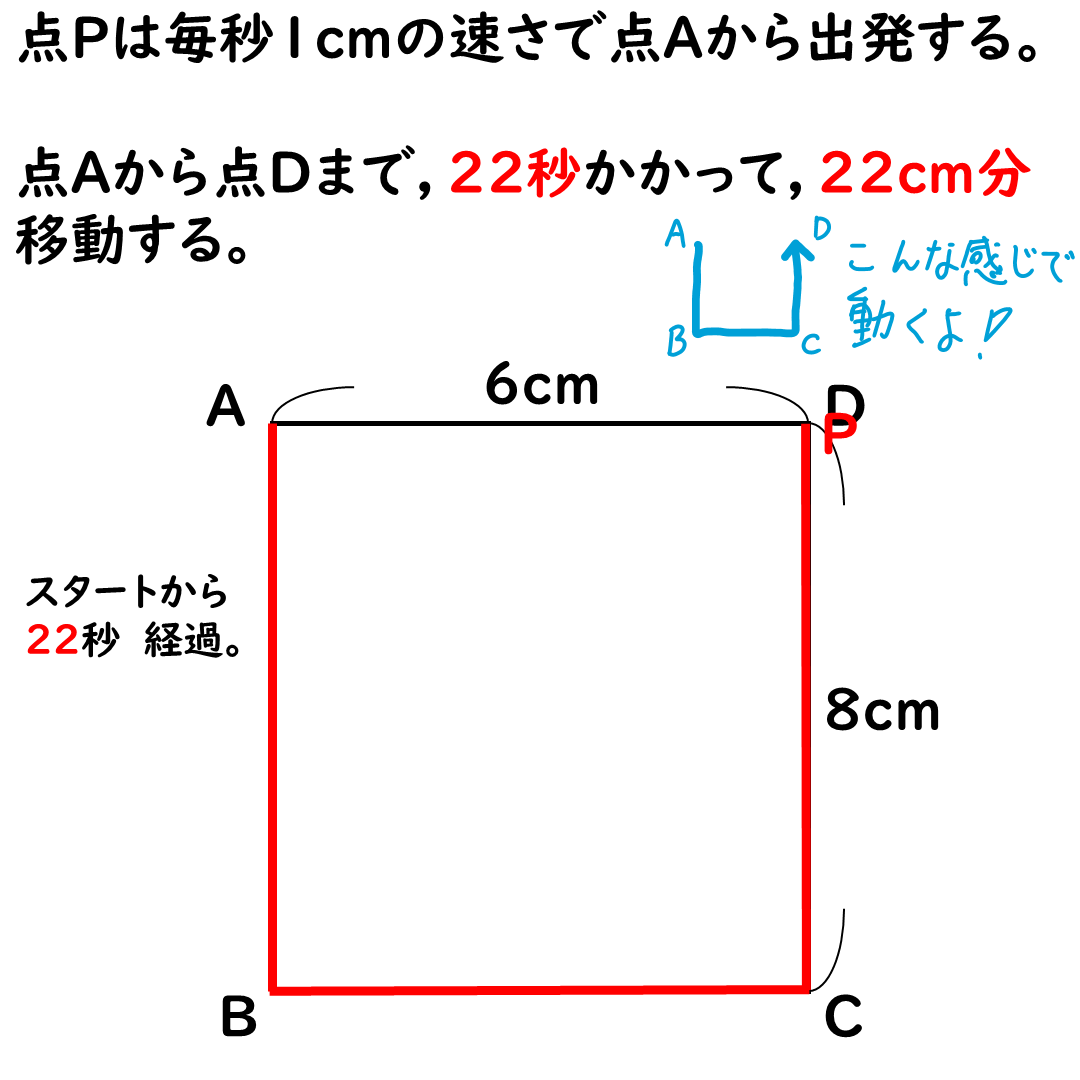
点Pは最大22cm移動する。
点Pって,最終的には点Dに
到着する。
点Aから点Dまでは,
22秒かかる。
移動距離は22cmだ。
この22cmが重要だ☆
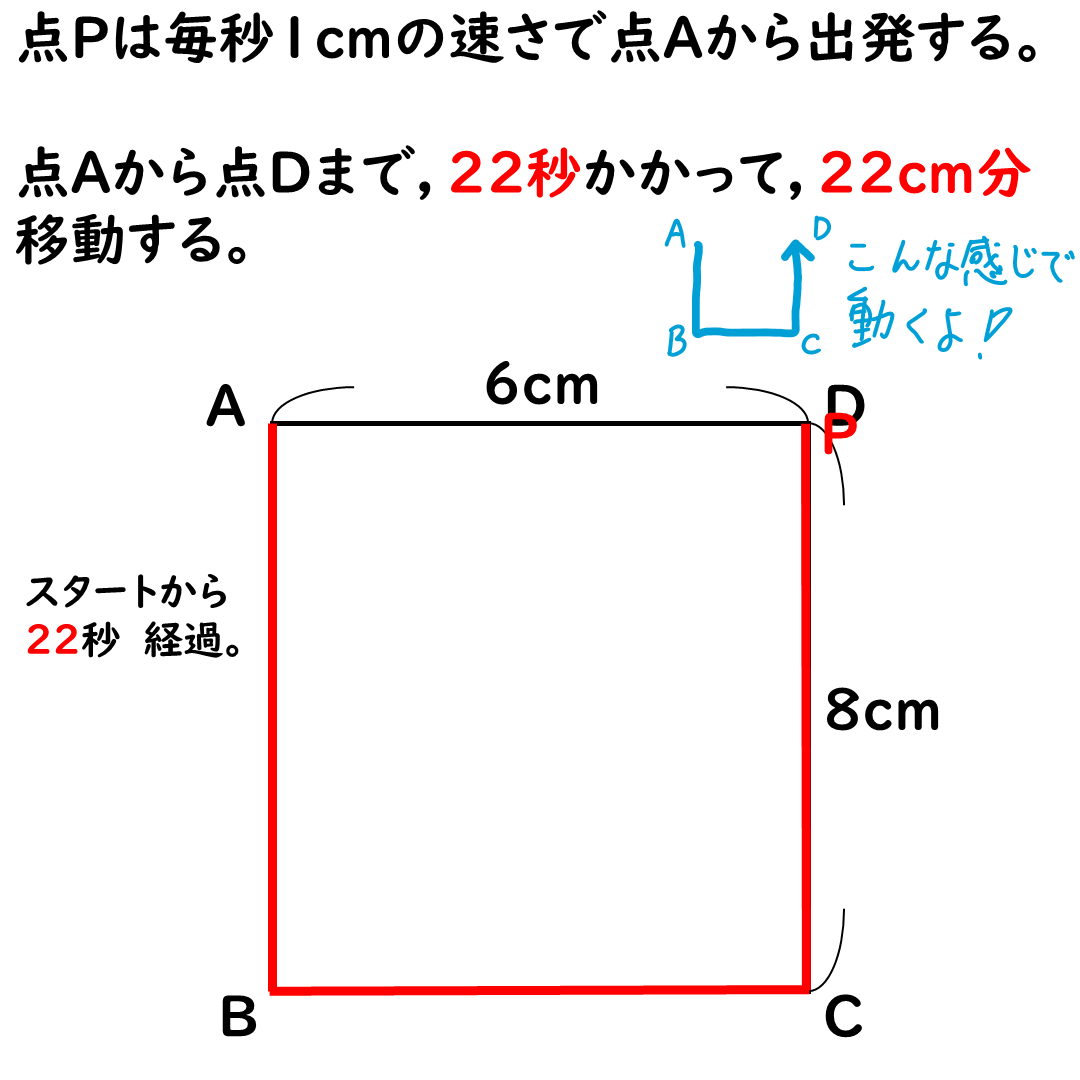
もう一度。
点Aから点Dまで行くのに,
22秒かかって。
22cm移動するよ!
Uの字みたいに移動するね。
答えはこちら
答えはこちらです。
丸付けしてみてね。

解説はこちら
ここからは,解説です。
まずは,①から順にやっていこうね。
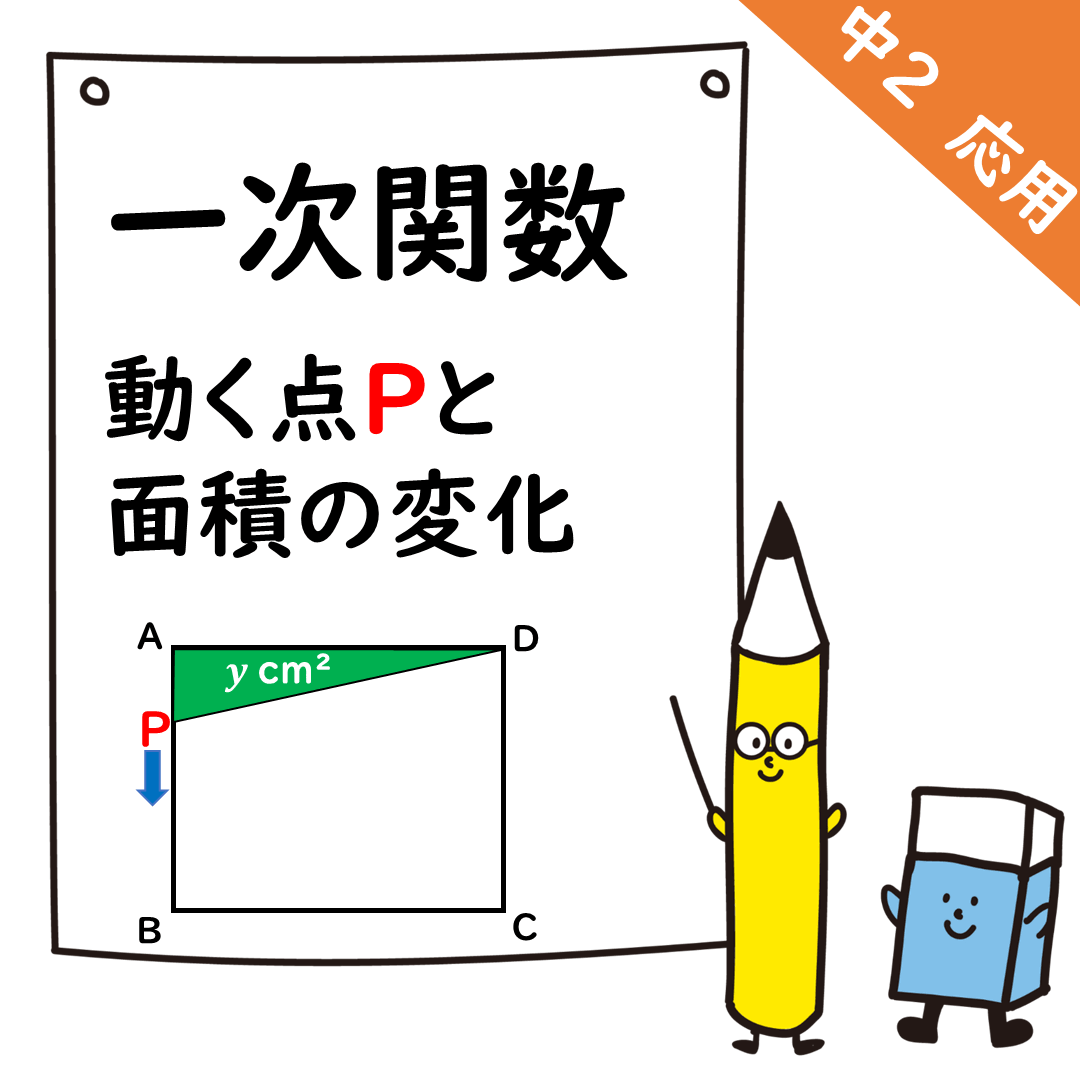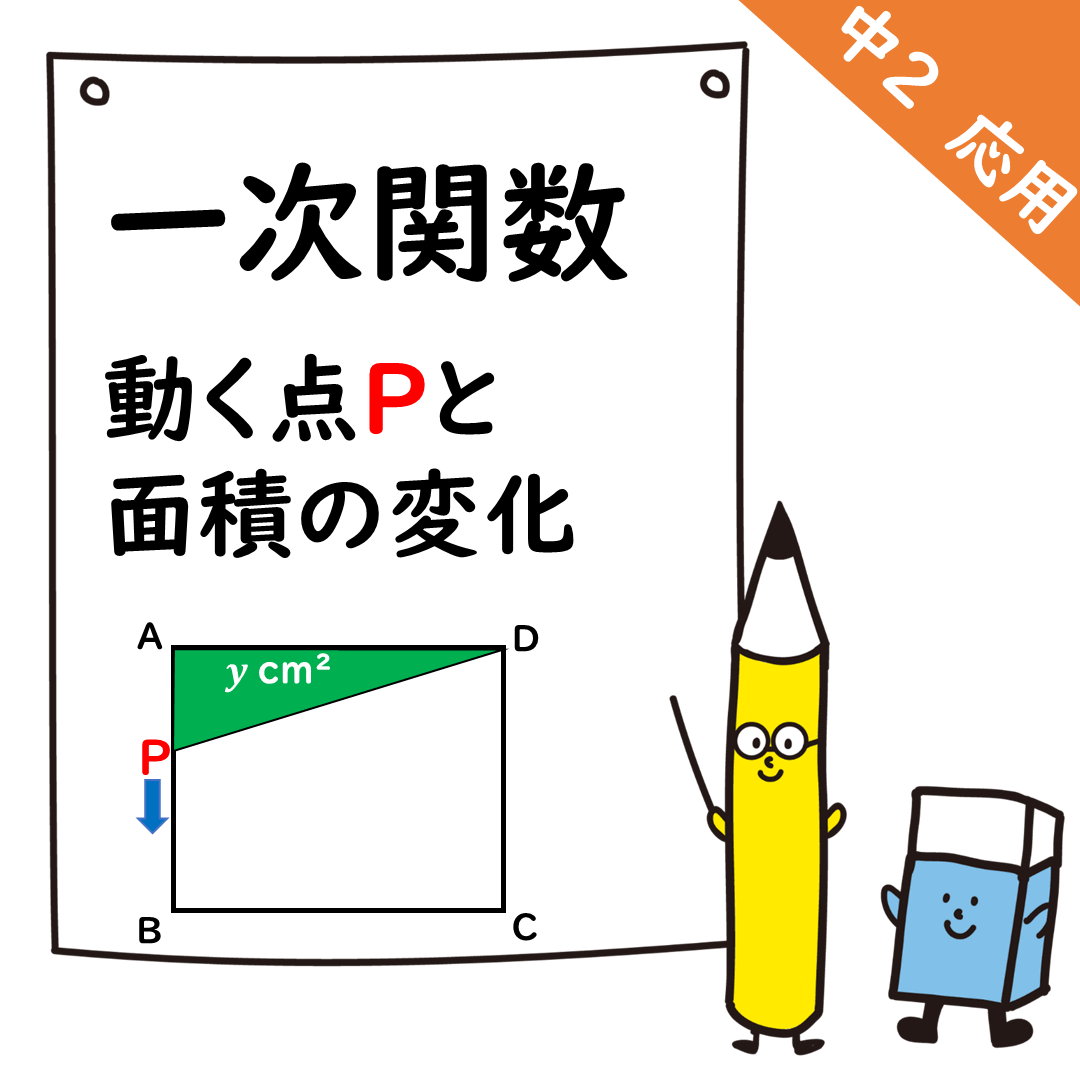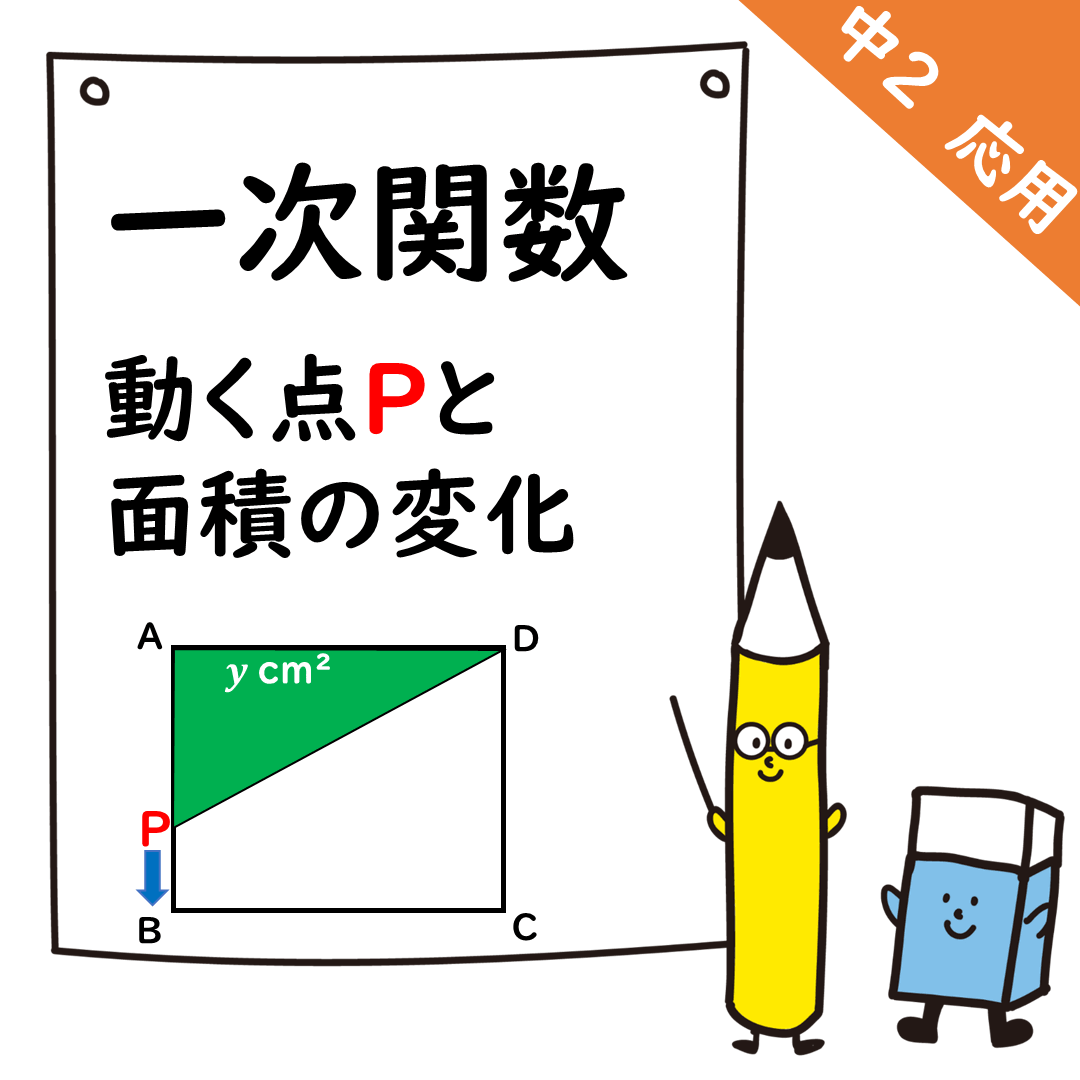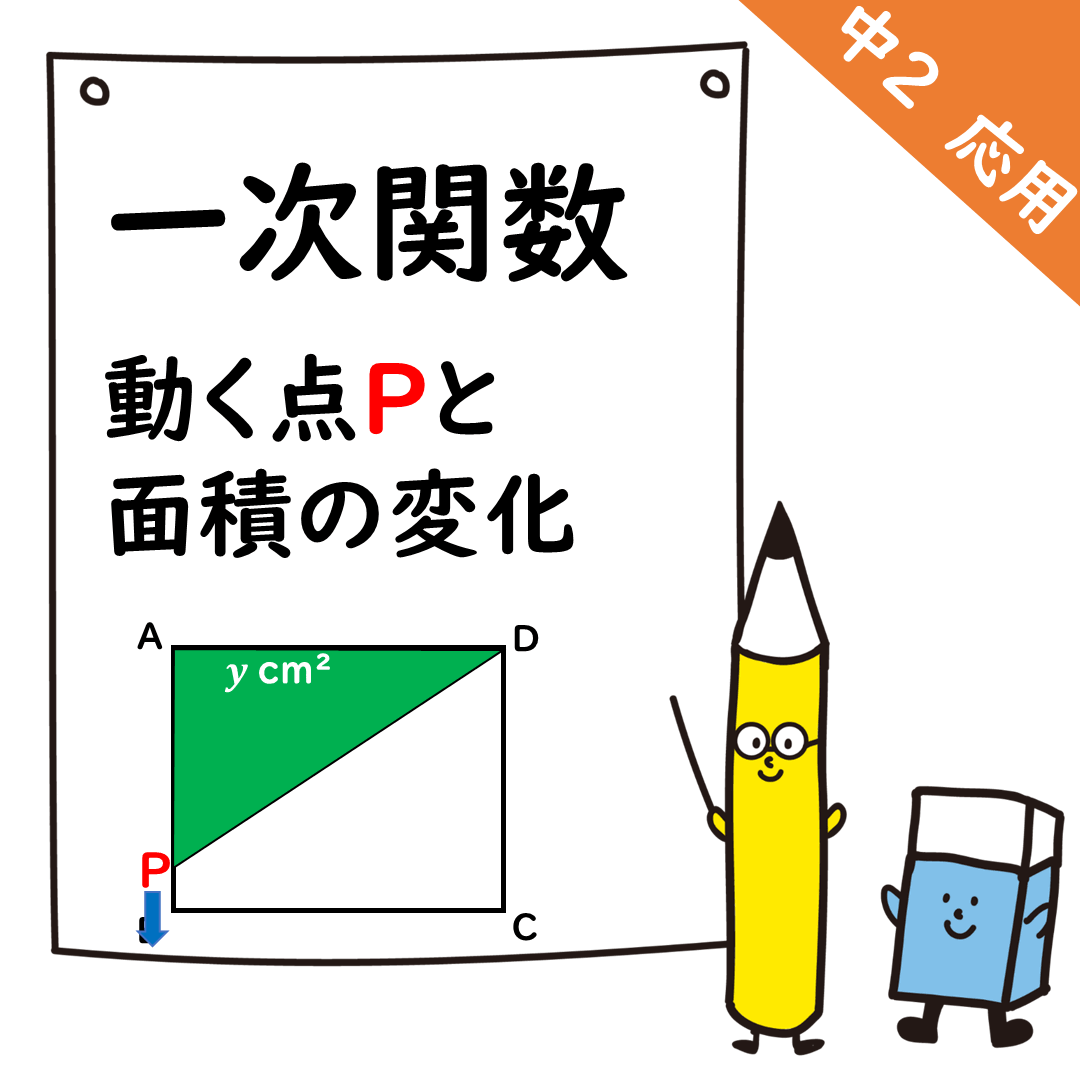
問① 辺AB上の動き
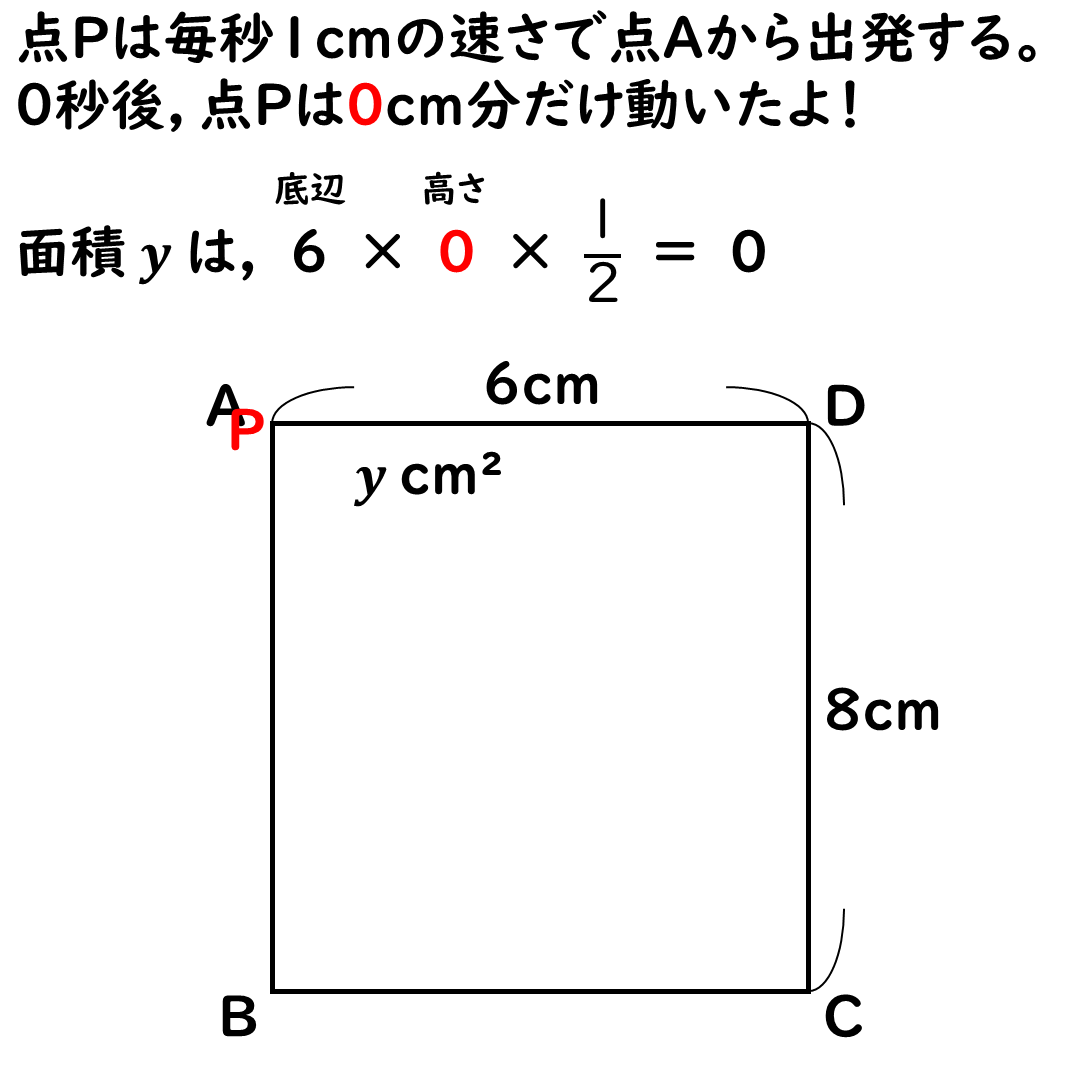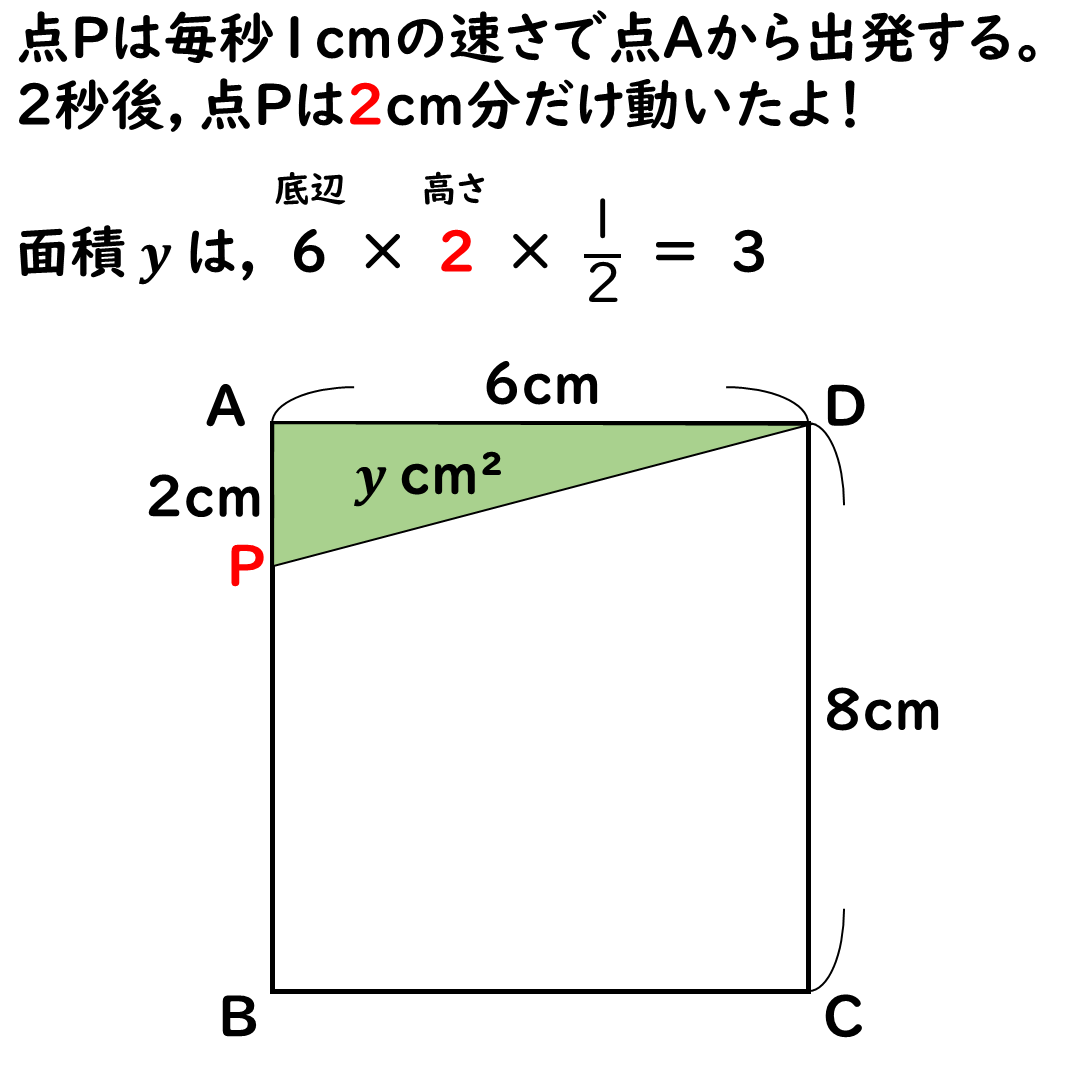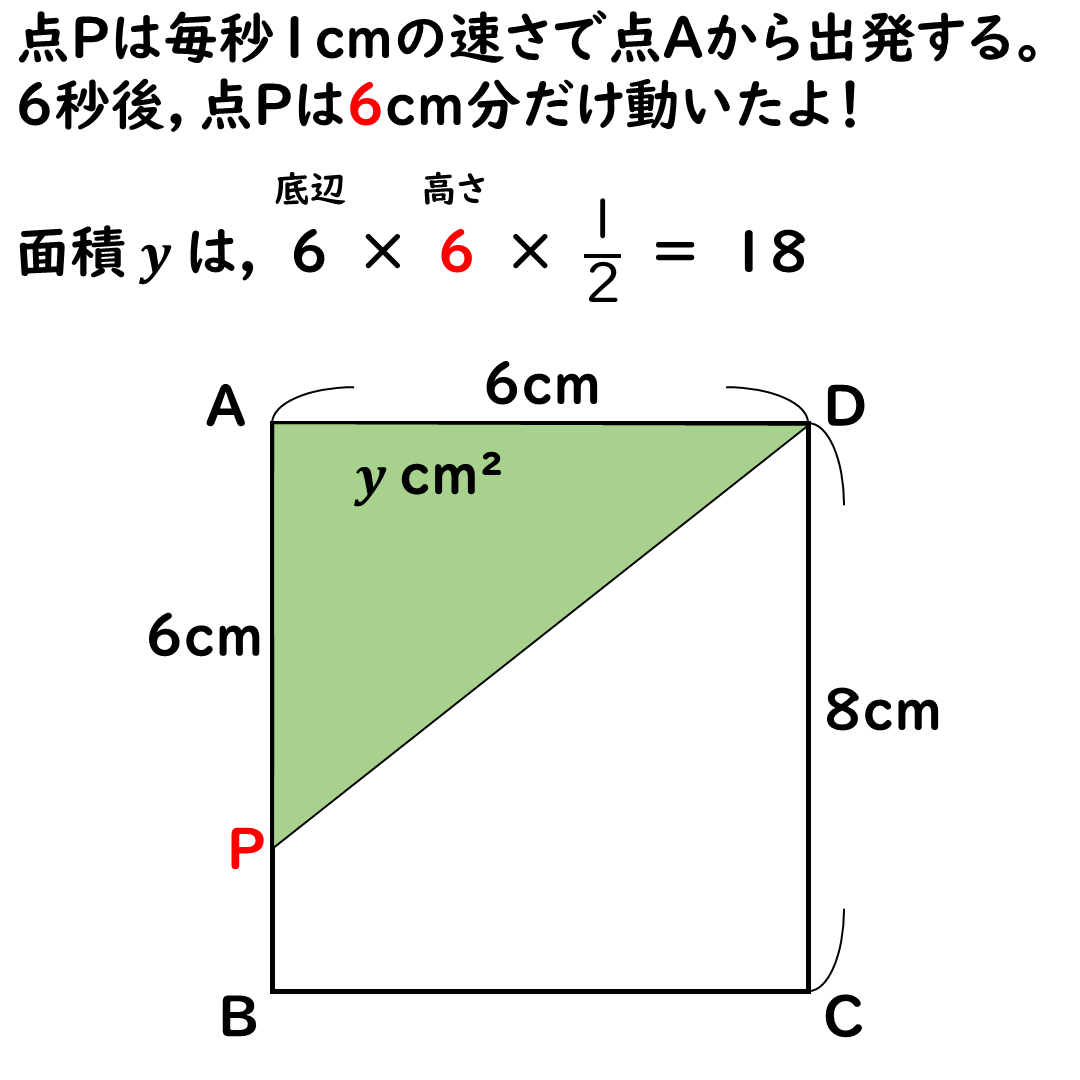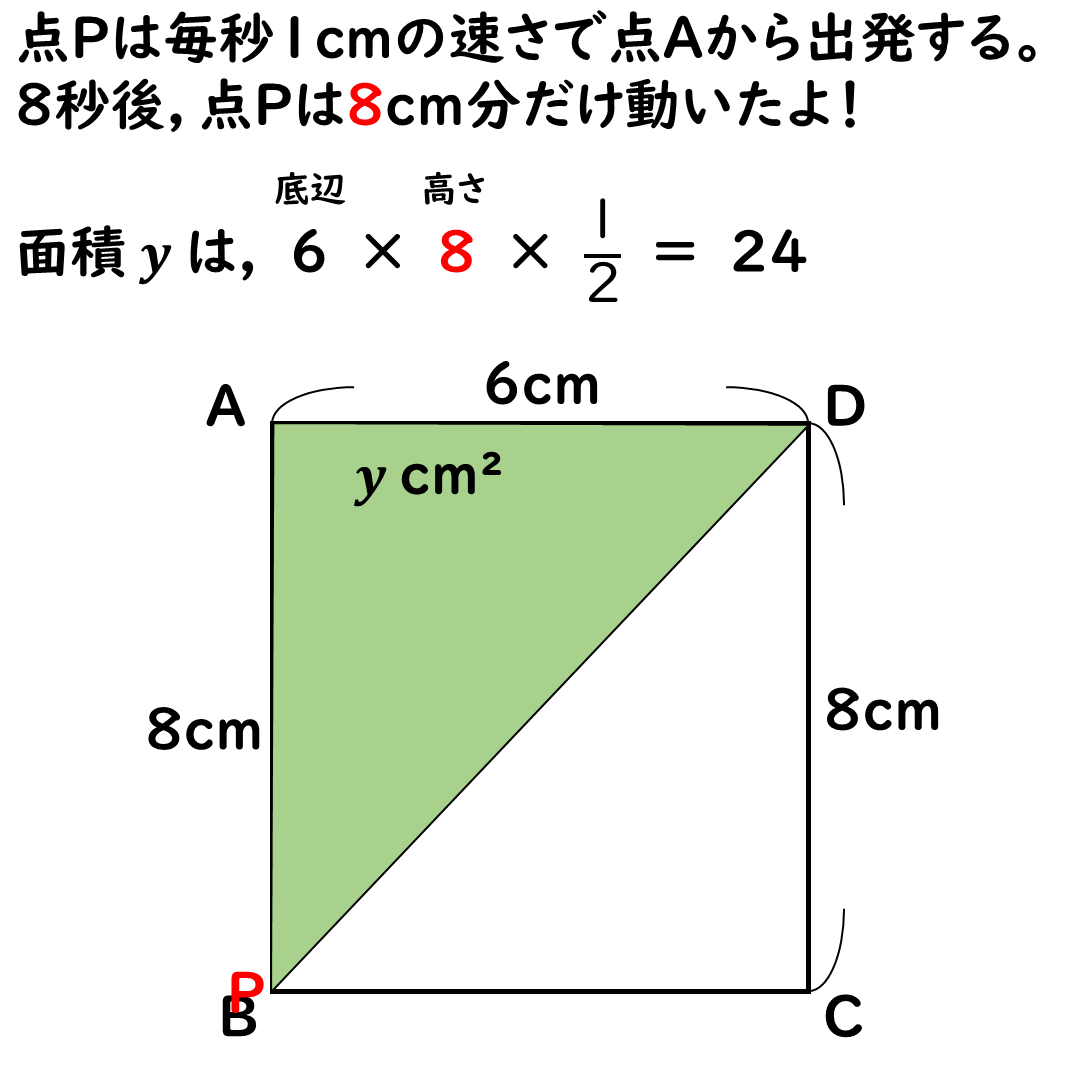
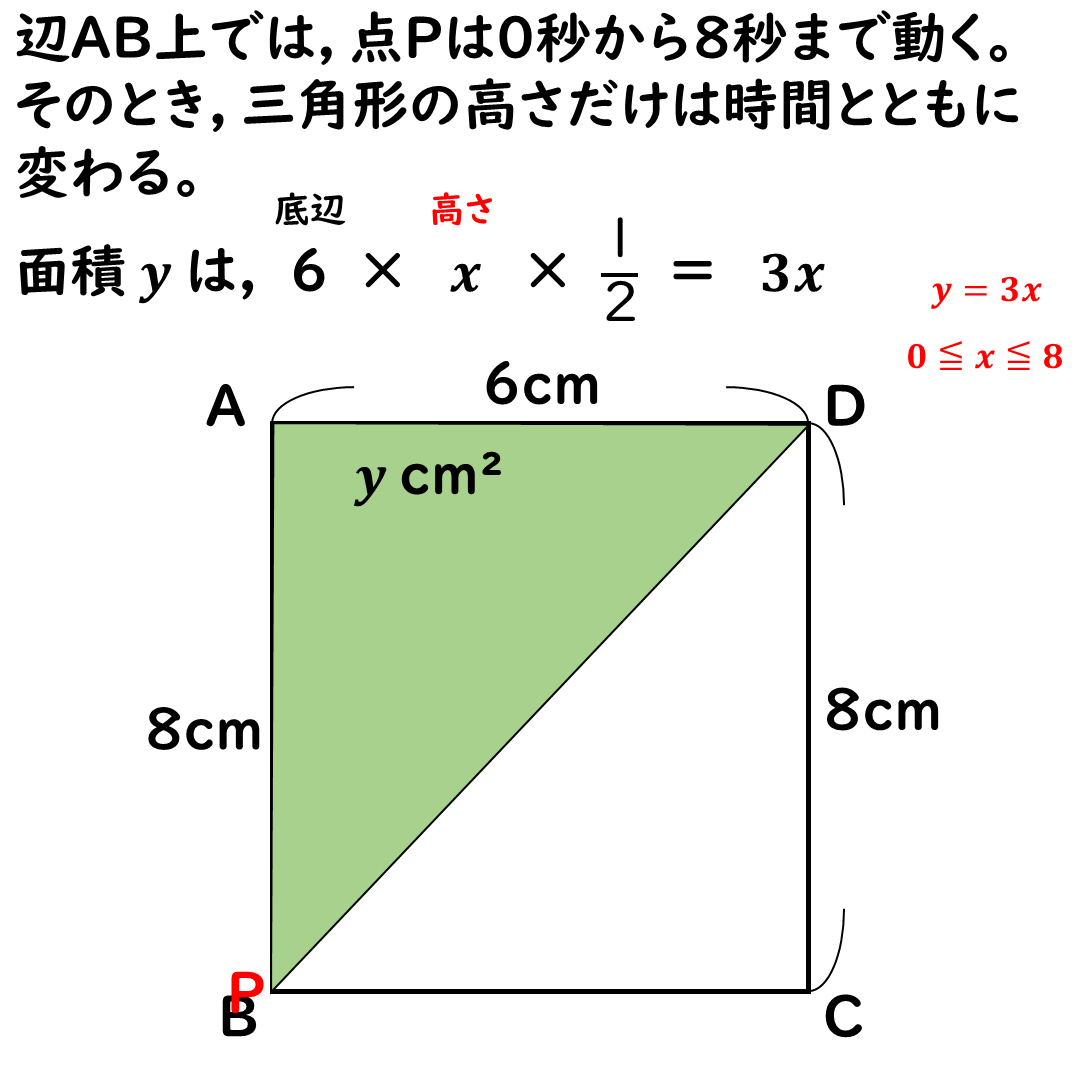
辺AB上では,
面積yはどんどん増えていく。
点Pは毎秒1cmで進む。
辺ADの6cmを底辺とすると,
高さは辺APだ。
その高さが時間とともに
増えていく。
高さAPは,
点Pの移動距離,つまり
xcmだ。
面積は三角形だから,
2で割るのを忘れずに。
そのときのxの変域は,
辺ABの長さ分だね。
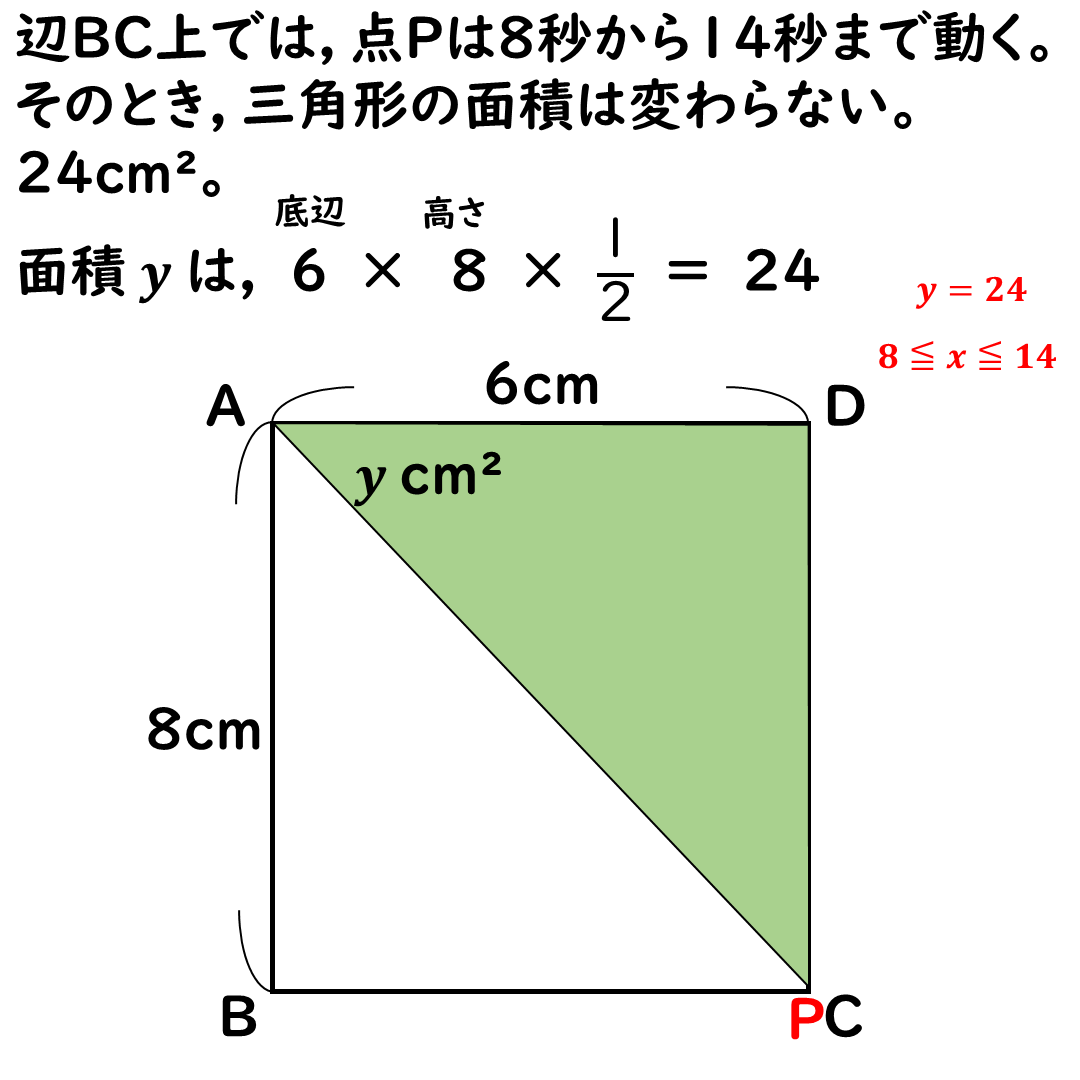
辺BC上の動き
これは問題にはなかったけど
やっておこう。
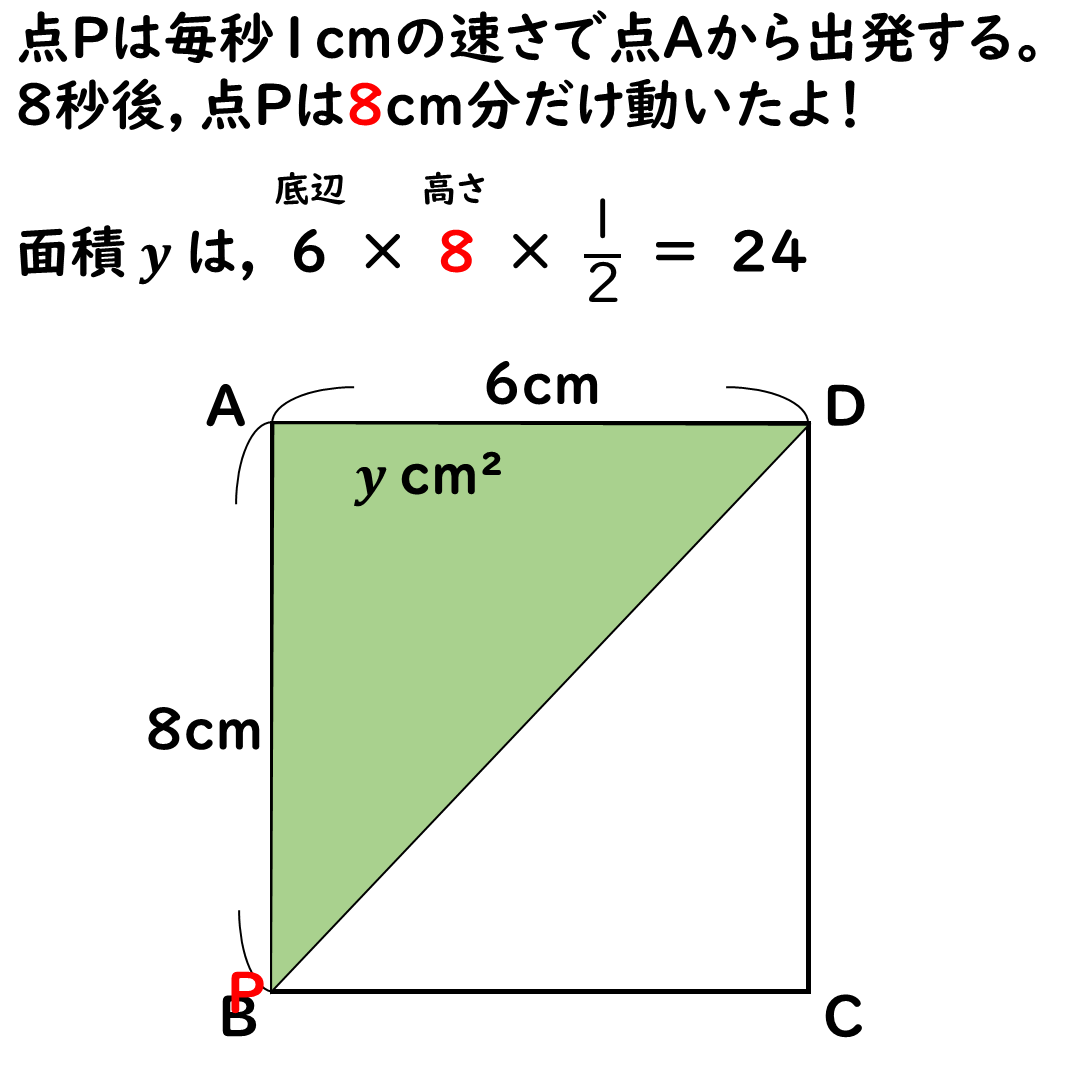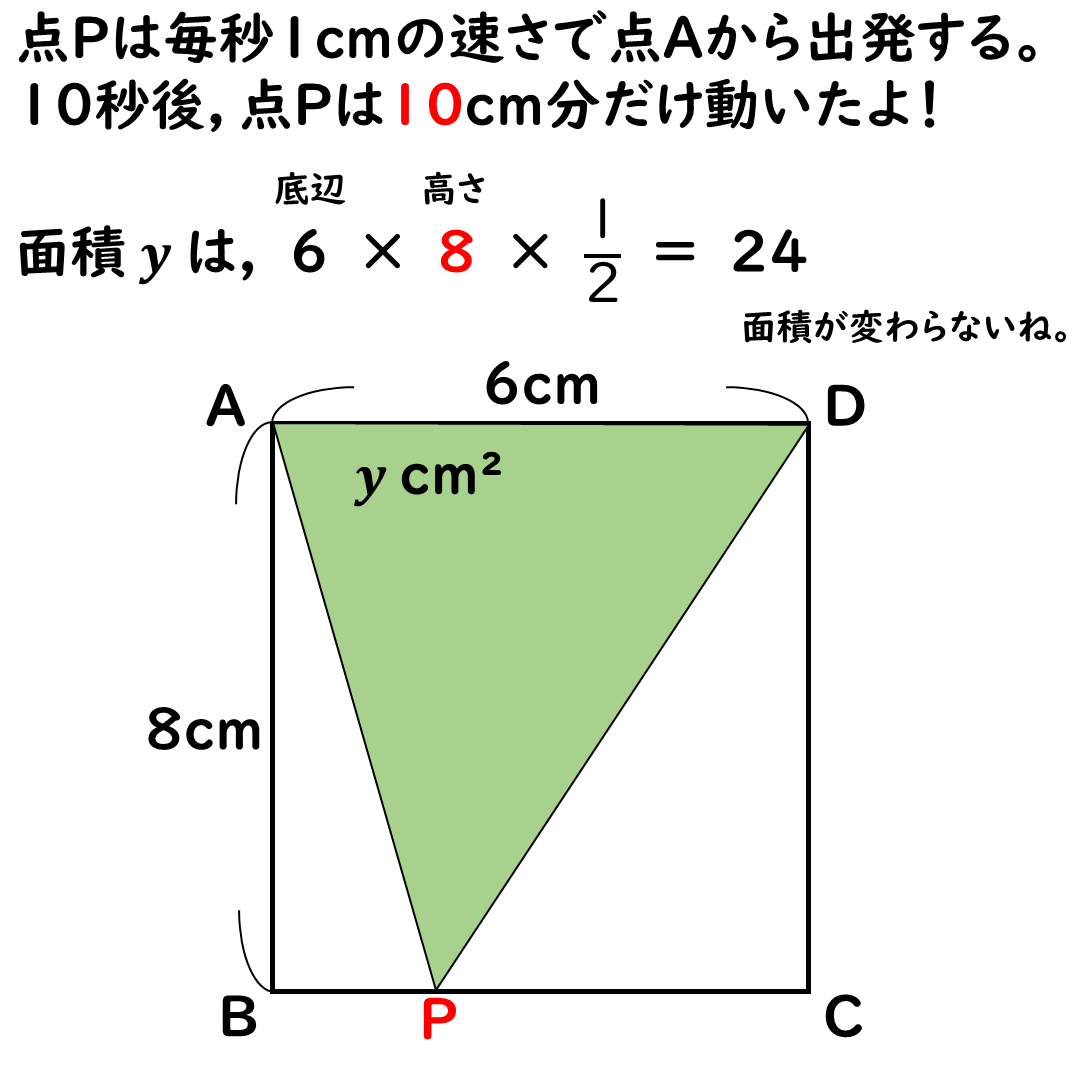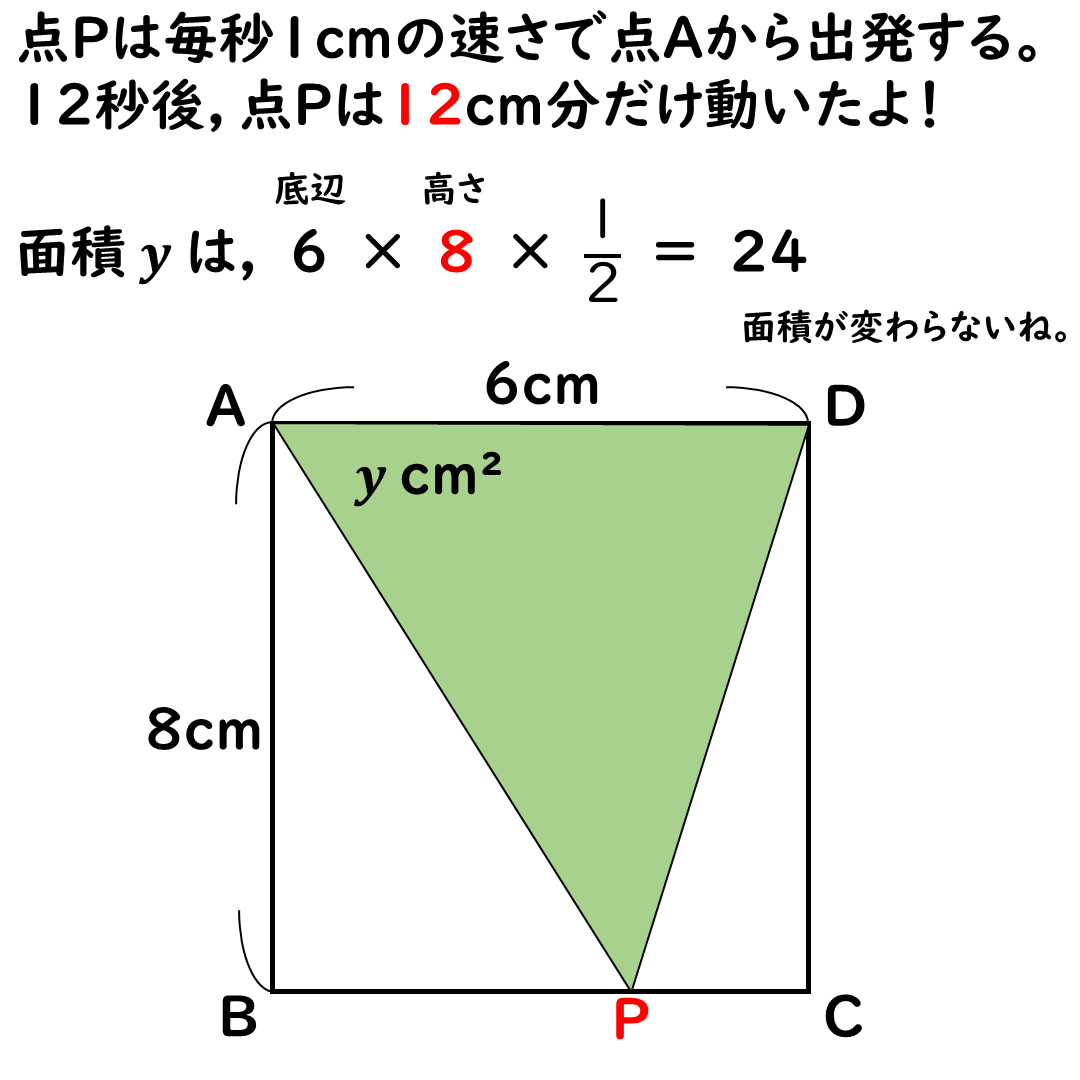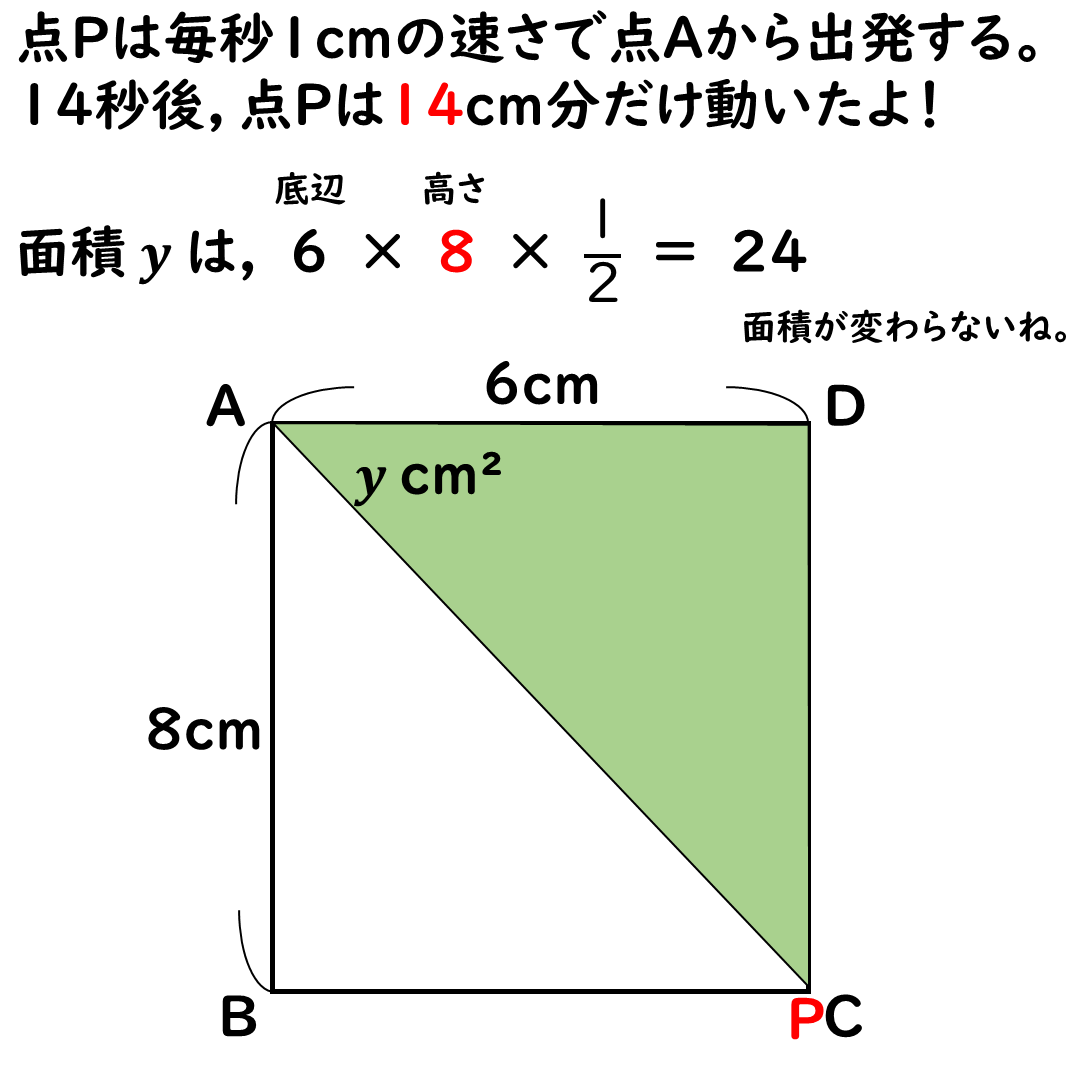
xの変域が8≦x≦14
のところでは
面積yは常に24cm2だ
三角形の形は変わるけど
底辺と高さが変わらないからね。
問② 辺CD上の動き
これが厄介なのかなと。
動きはこんな感じだ。
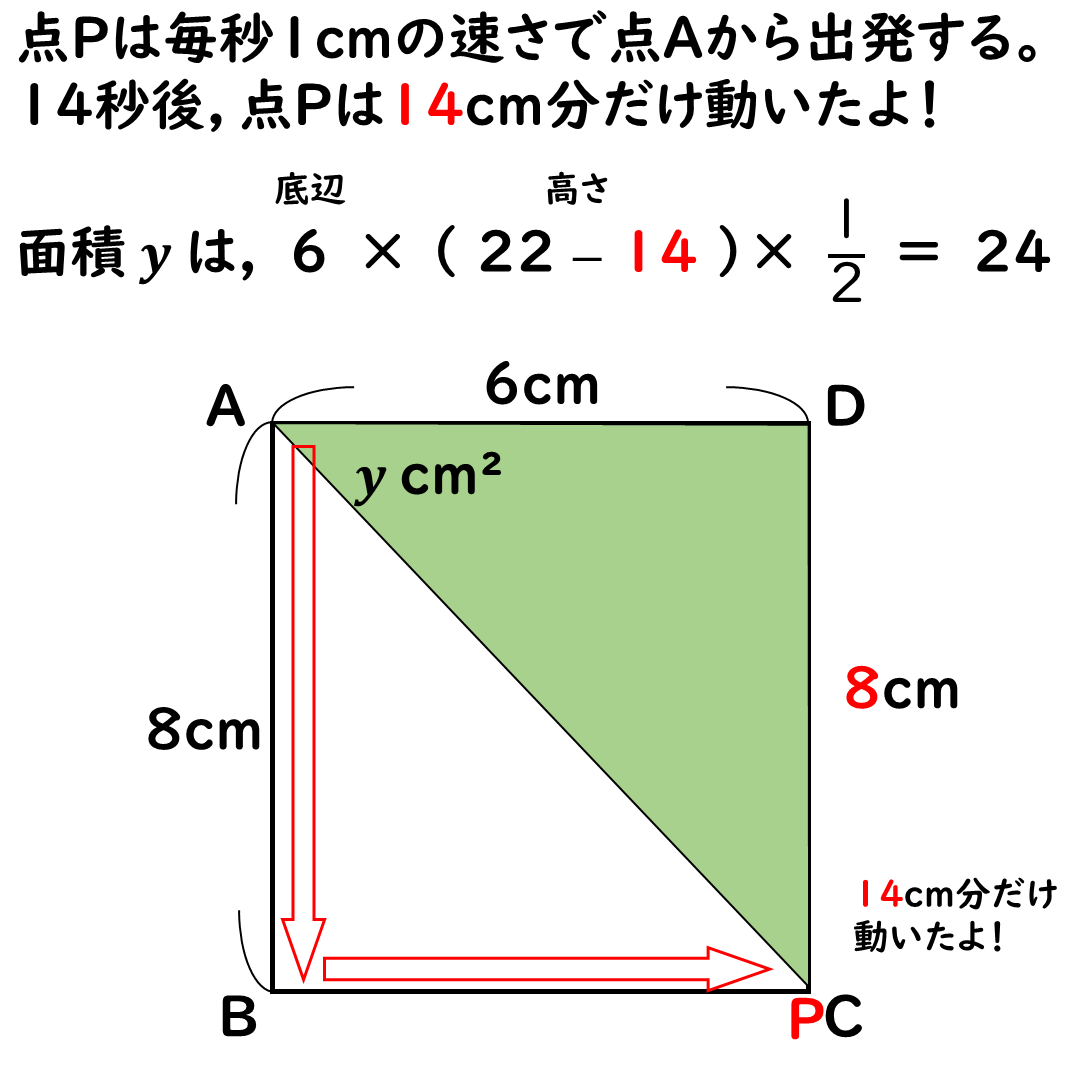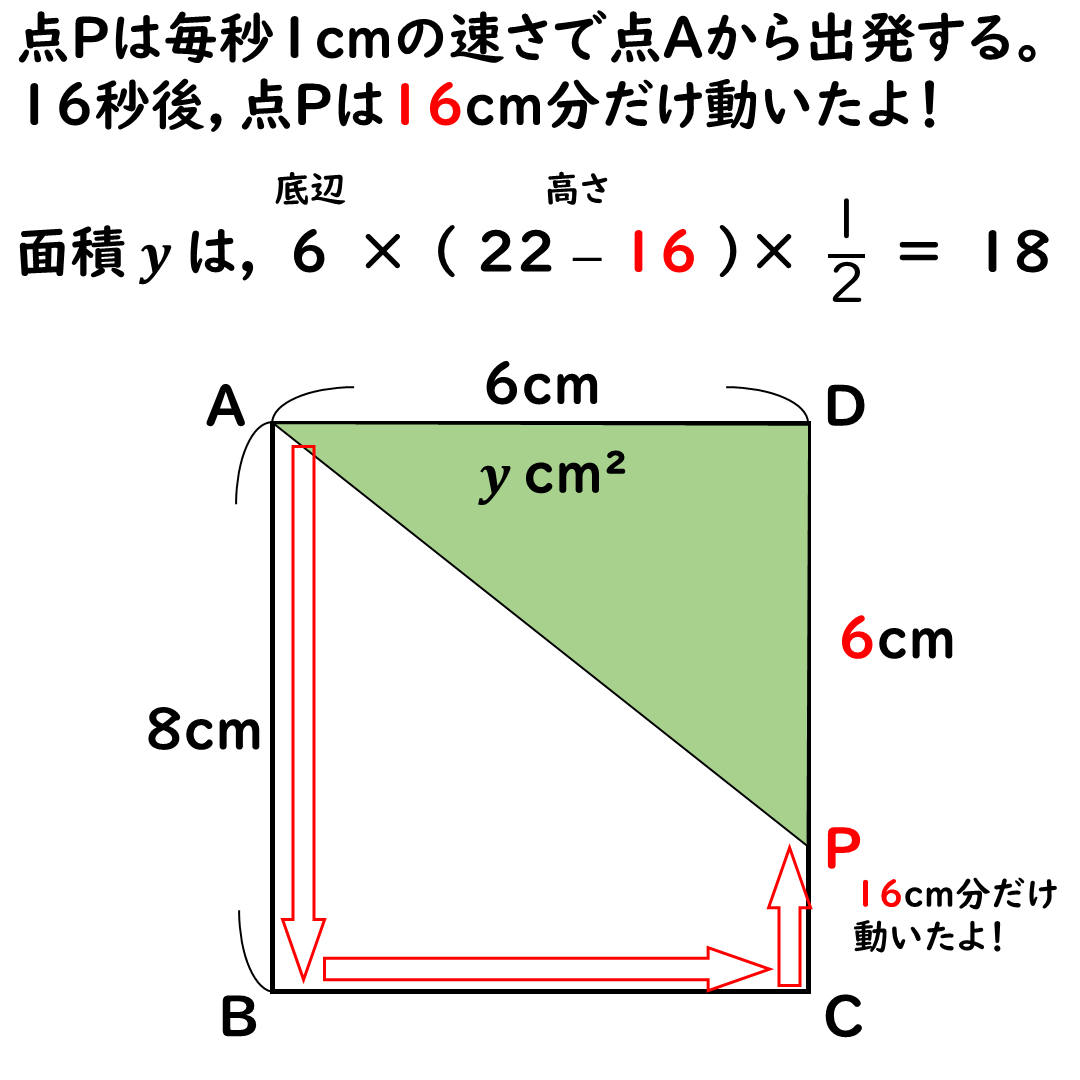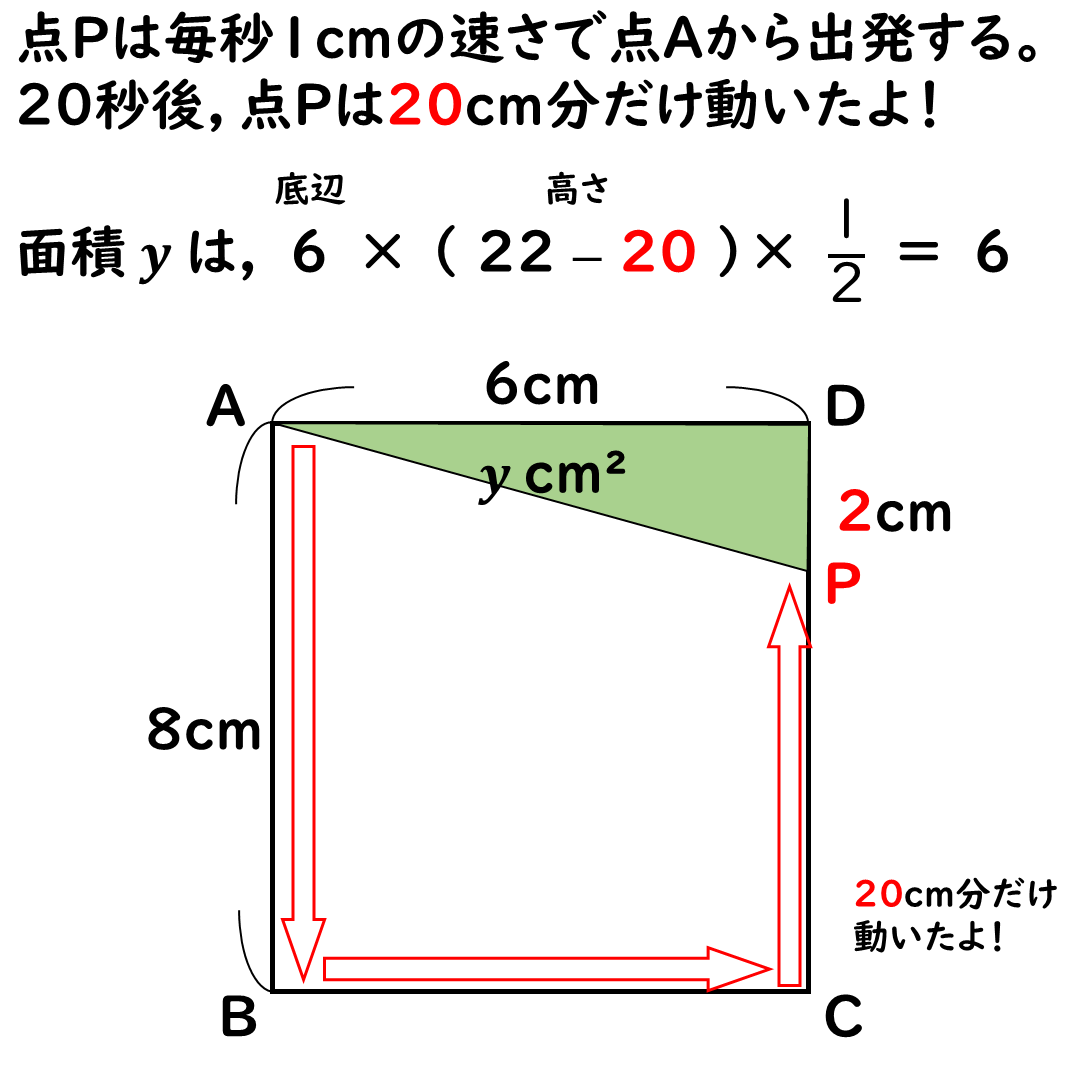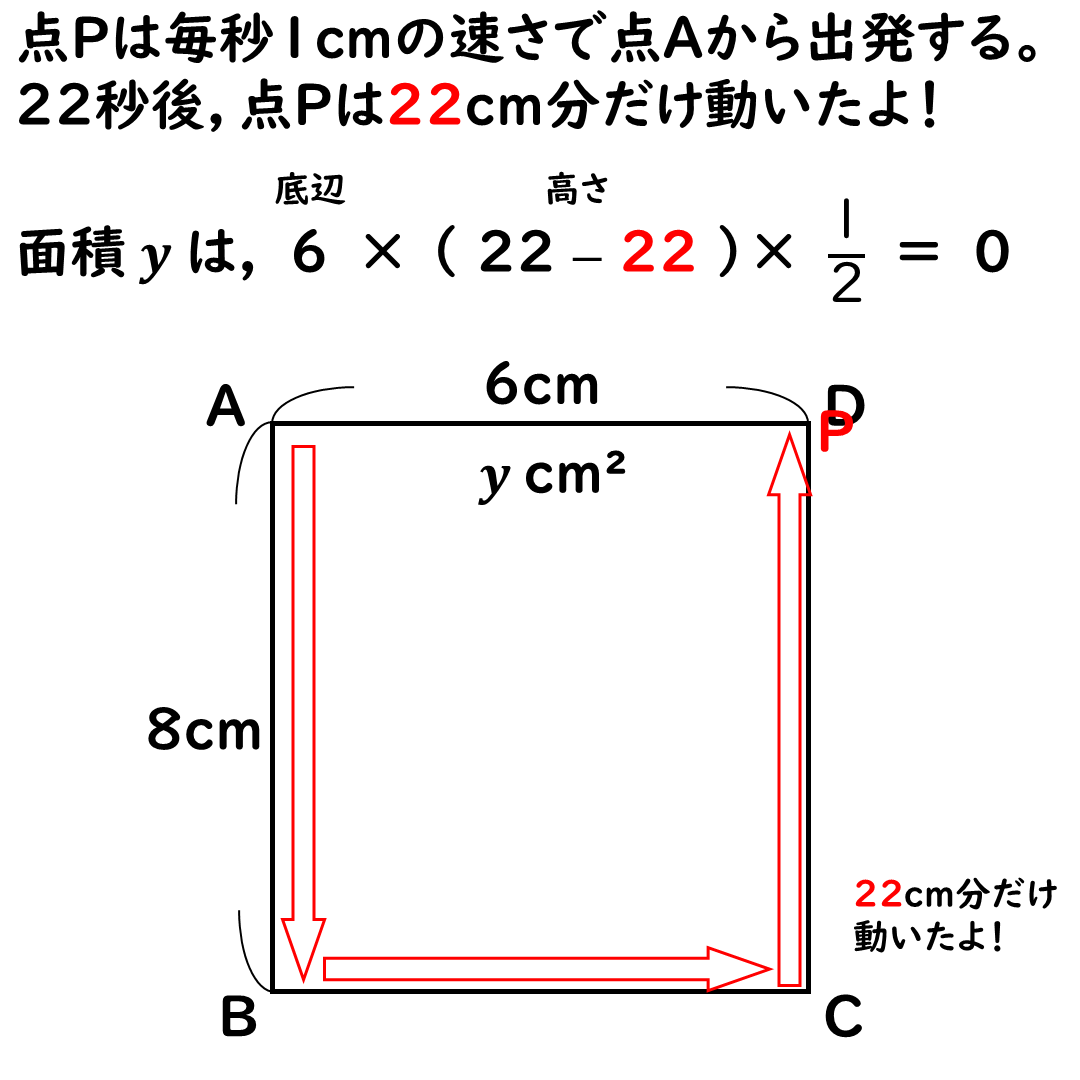
面積yは徐々に減っていき,
点Pが点Dに到着すると
面積は0になる。
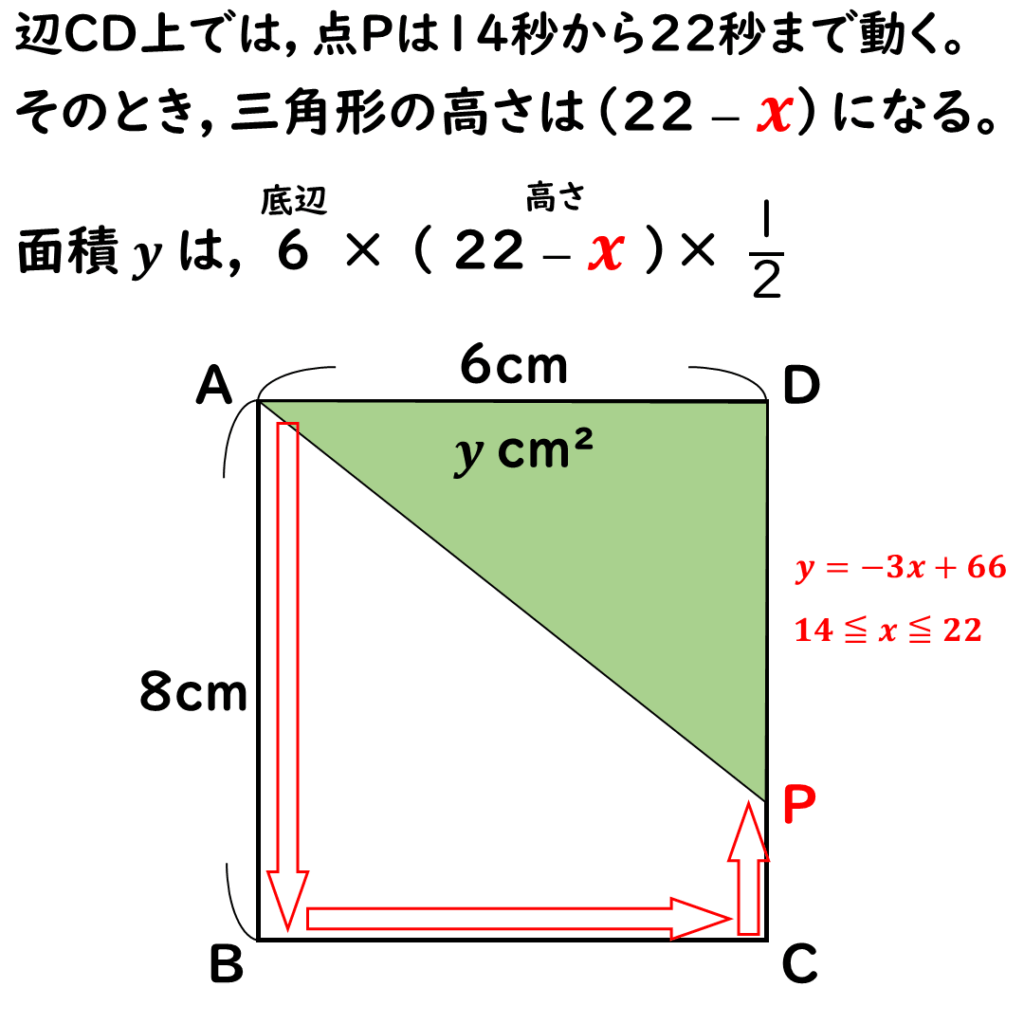
三角形の底辺を辺AD
とすると,
高さは辺DPだ。
これがなかなか曲者。
でも,
ここで,ヒントにあった,
点Pの最大移動距離
22cmを使うよ。
わかる人はOK。
わからん人はヒントまで戻ってね。
点Pは,点Aから出発して
点Dまでに最大22cmを
移動するのだ。
Uの字みたいに移動するの。
その22cmから,
点Pがこれまで進んできた距離である
xcmをひき算すれば
高さDPの長さが出せる。
Uの字22cm ー xcm
だね。
そのときのxの変域は
14≦x≦22だ。
これも間違えやすいから注意だ。
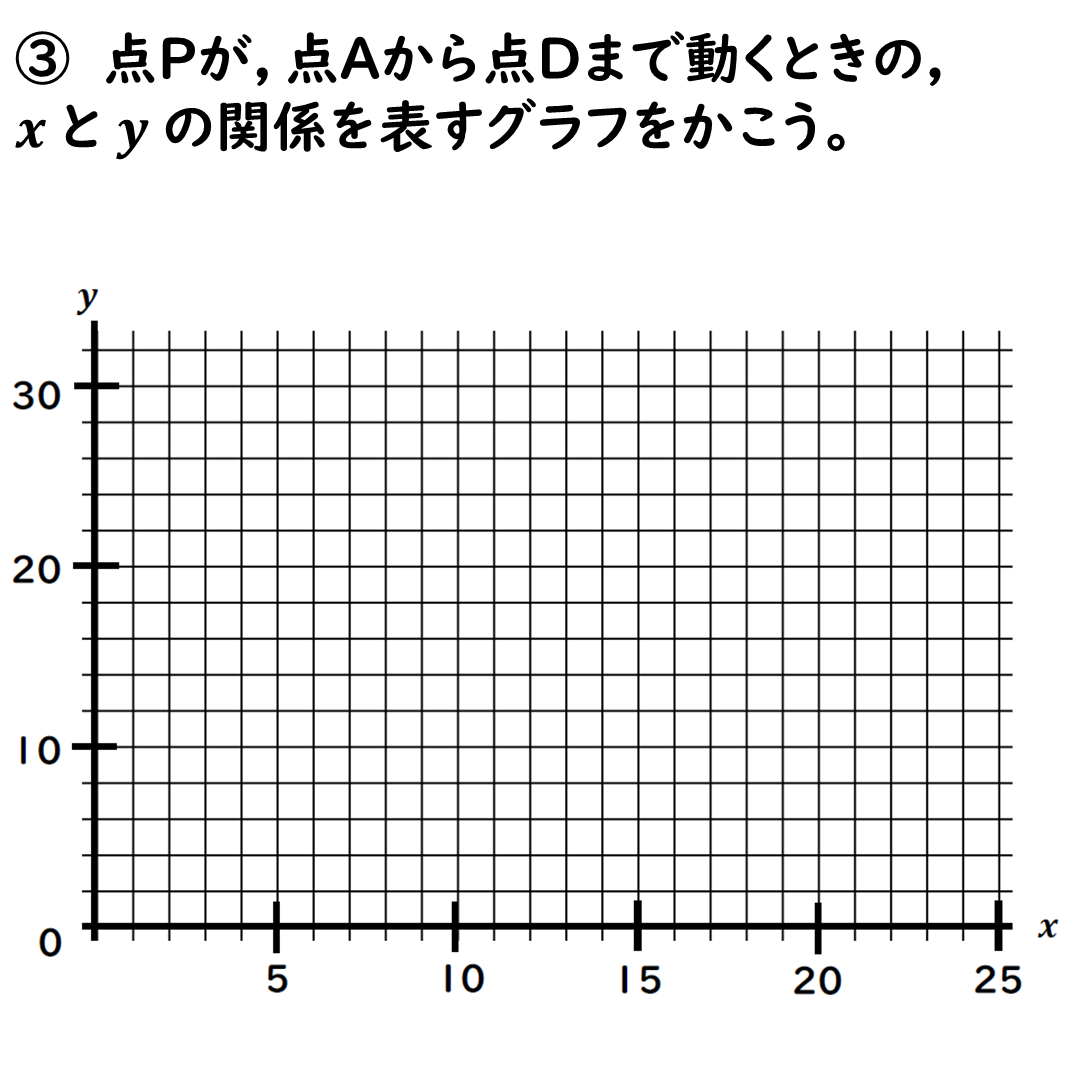
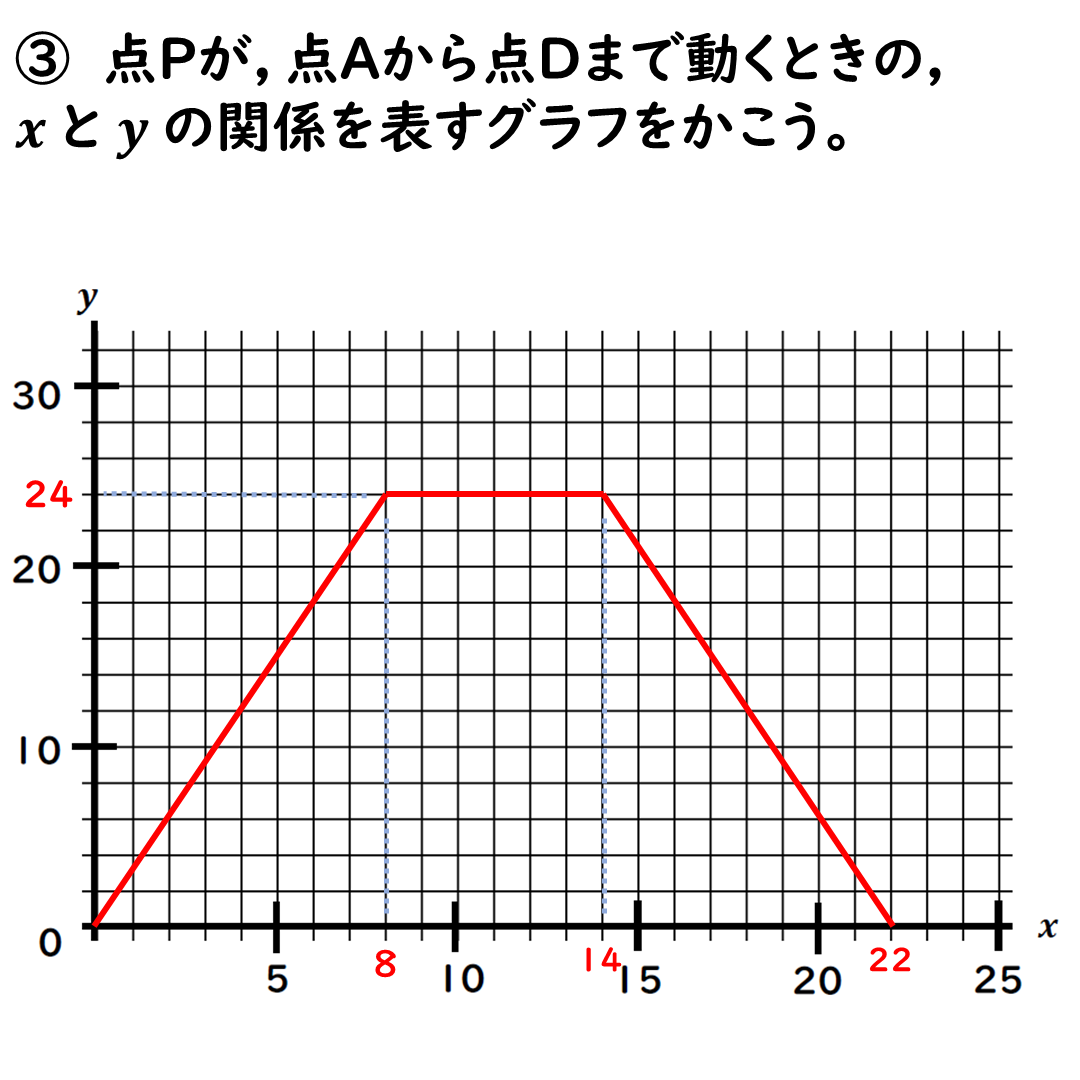
問③ yとxの関係をグラフにする
たぶん,一次関数は
中2の2学期中間テスト範囲だ。
一次関数の利用までは
テスト範囲に入らない場合,
2年2学期期末テストにこっそり
入ってくる。
いずれにしても,
学校の中間・期末テストでは
このグラフ問題までが
セットで出題の可能性が高い。
特に,授業で学んだ場合は
出やすいだろう。
実力テストとかだと,
グラフを書かせるところまでは
あんまり出ない印象。
どんなグラフになるかの4択問題は
あるかもね。
さて,解説にいこう。
といっても・・・
これまでの直線の式を
グラフにするだけである。
まずは辺AB上のグラフ。
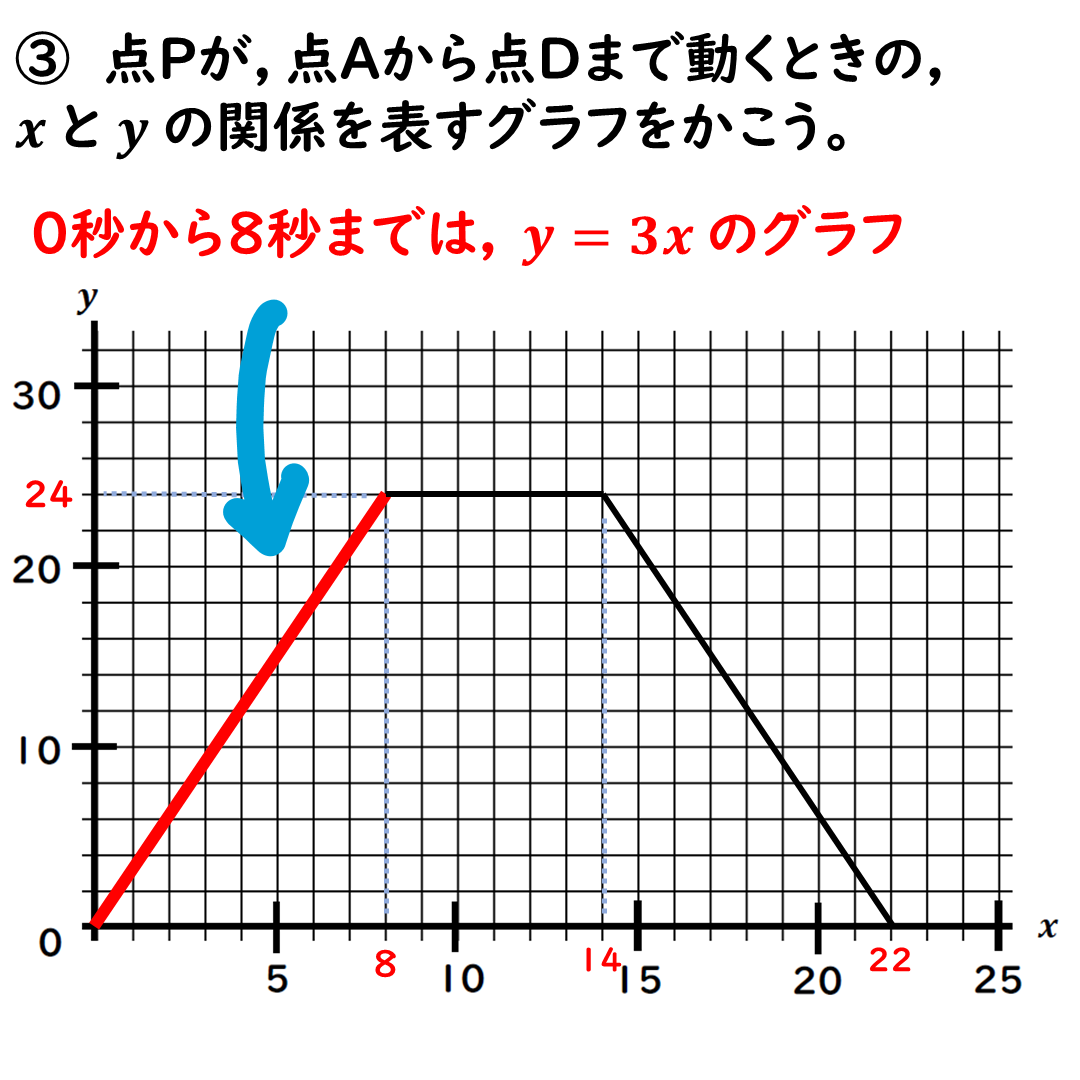
続いて,
辺BC上。
8≦x≦14で
y=24だね。
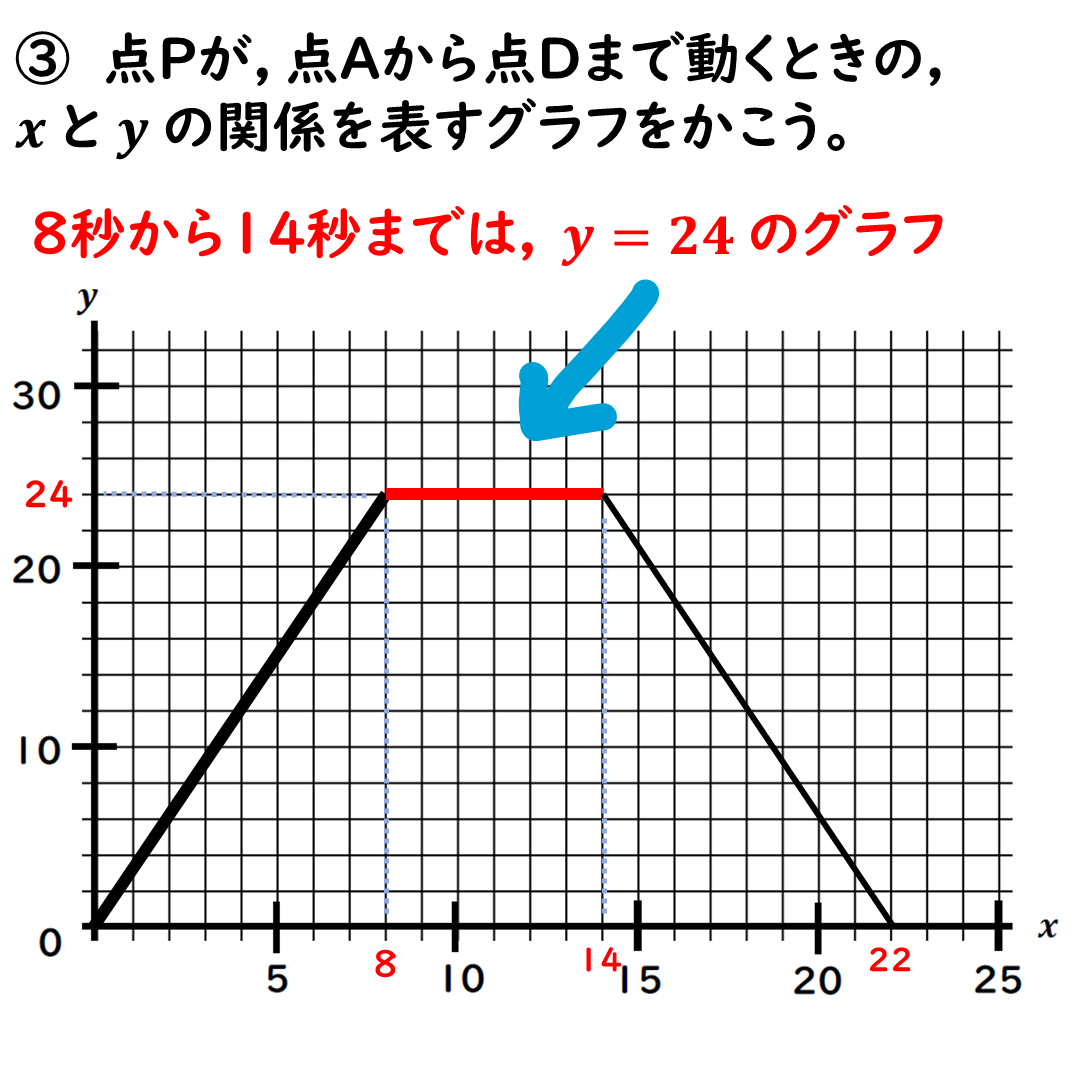
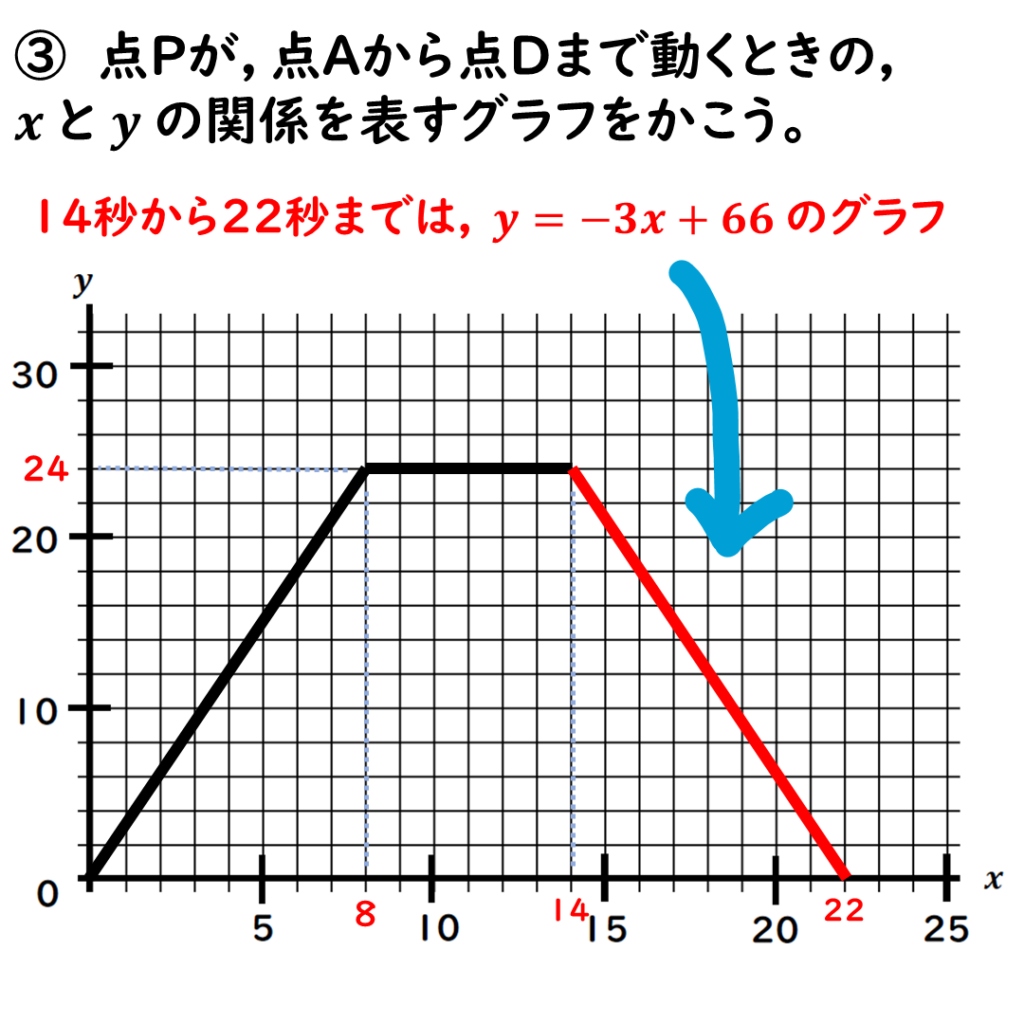
最後は辺CD上だ。
14≦x≦22の
範囲なんだけども。
最後は面積0になるので
x=22のとき,y=0
の点を取って線でつなごう。
実は,この辺CD上のグラフの作図
で気付いてほしいことがある。
簡単な式の求め方がある。
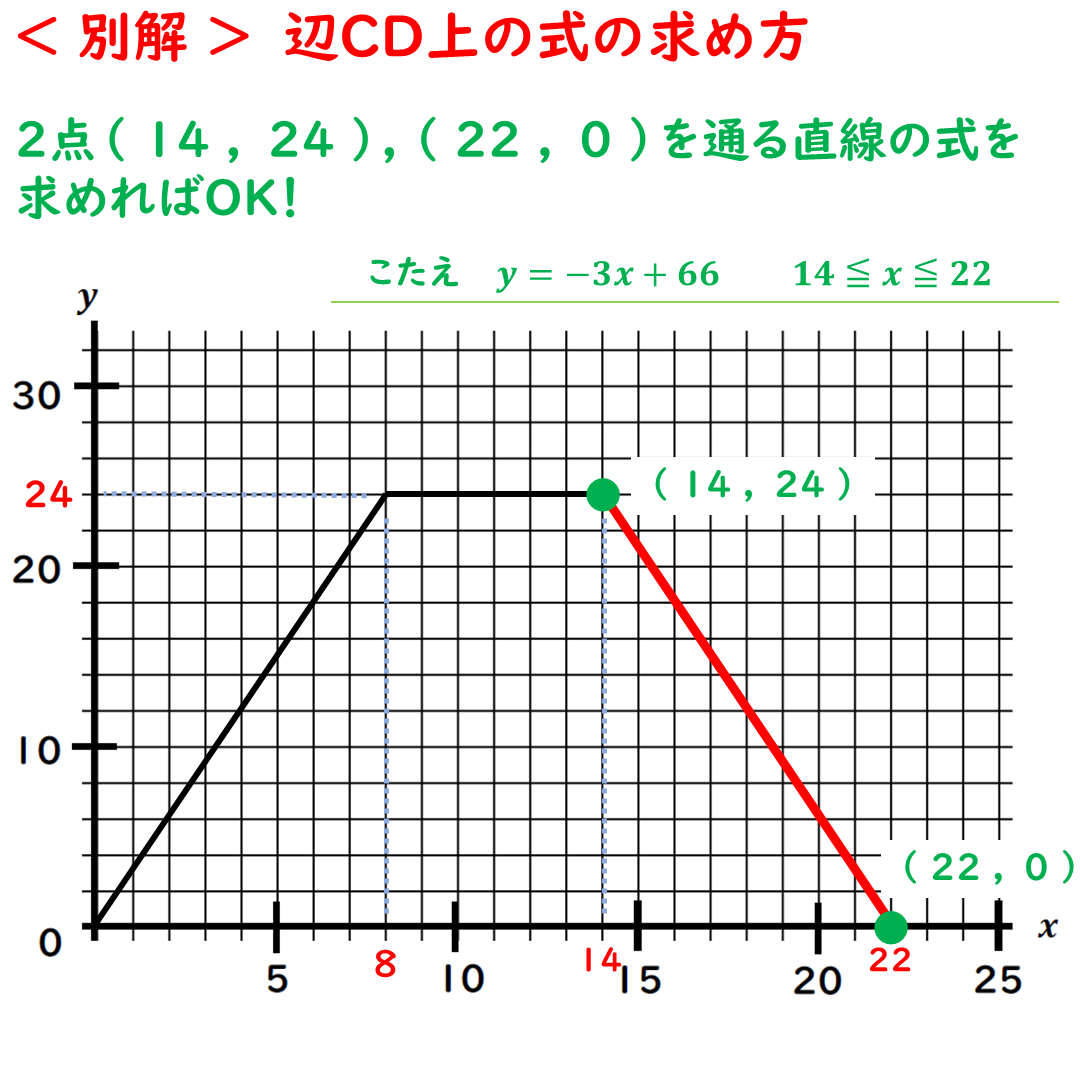
【別解】辺CD上の動き
点Pが辺CD上を動くときが
なかなか厄介だ。
でも実は,
点Pの動きをしっかり
見なくても解ける。
辺CD上の2点を
見るだけでOKなのだ。
それは,辺CD上の
最初と最後の2点だ。
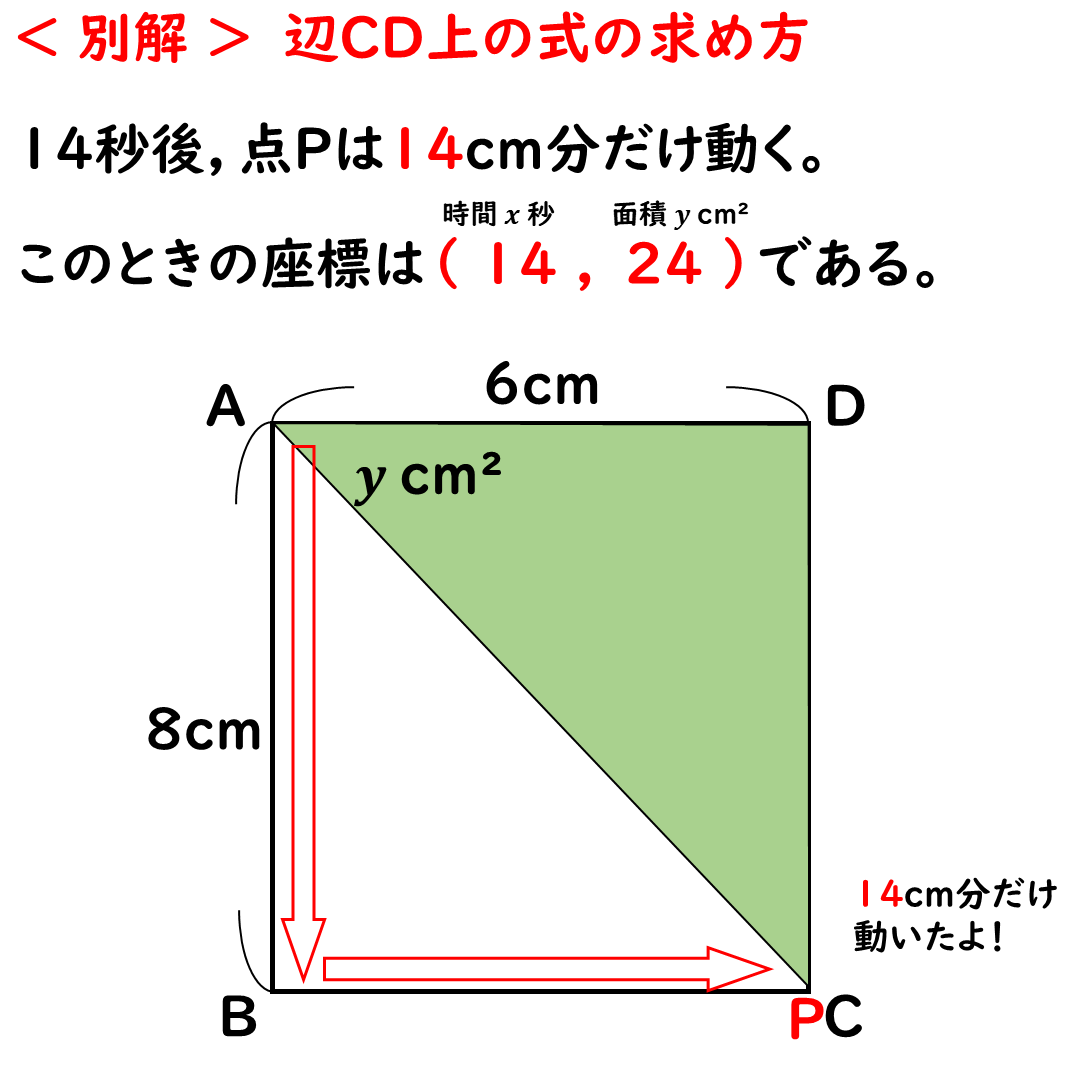
まずは辺CD上の最初。
点Pが点C上に重なるとき。
このときの座標は
(14,24)だ。
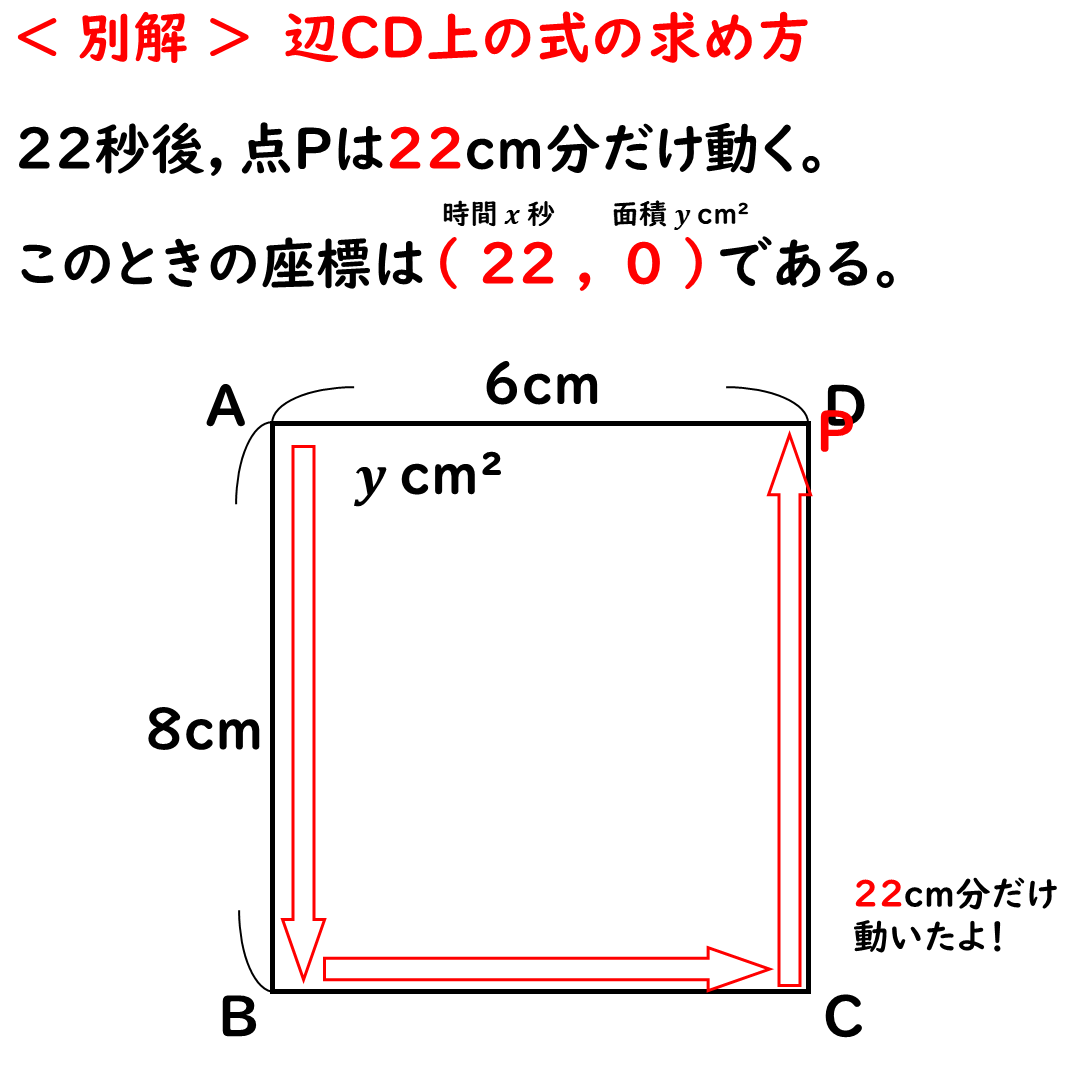
次に,最後の2点目。
点Pが点Dと重なるときだ。
22秒後,面積y=0になる。
座標は(22,0)だ。
よって,
辺CD上の式というのは,
次のように言い換えられる。
2点(14,24)(22,0)
を通る直線の式。
変域は14≦x≦22だ。
グラフも,この2点を
結ぶ線でOKだ。
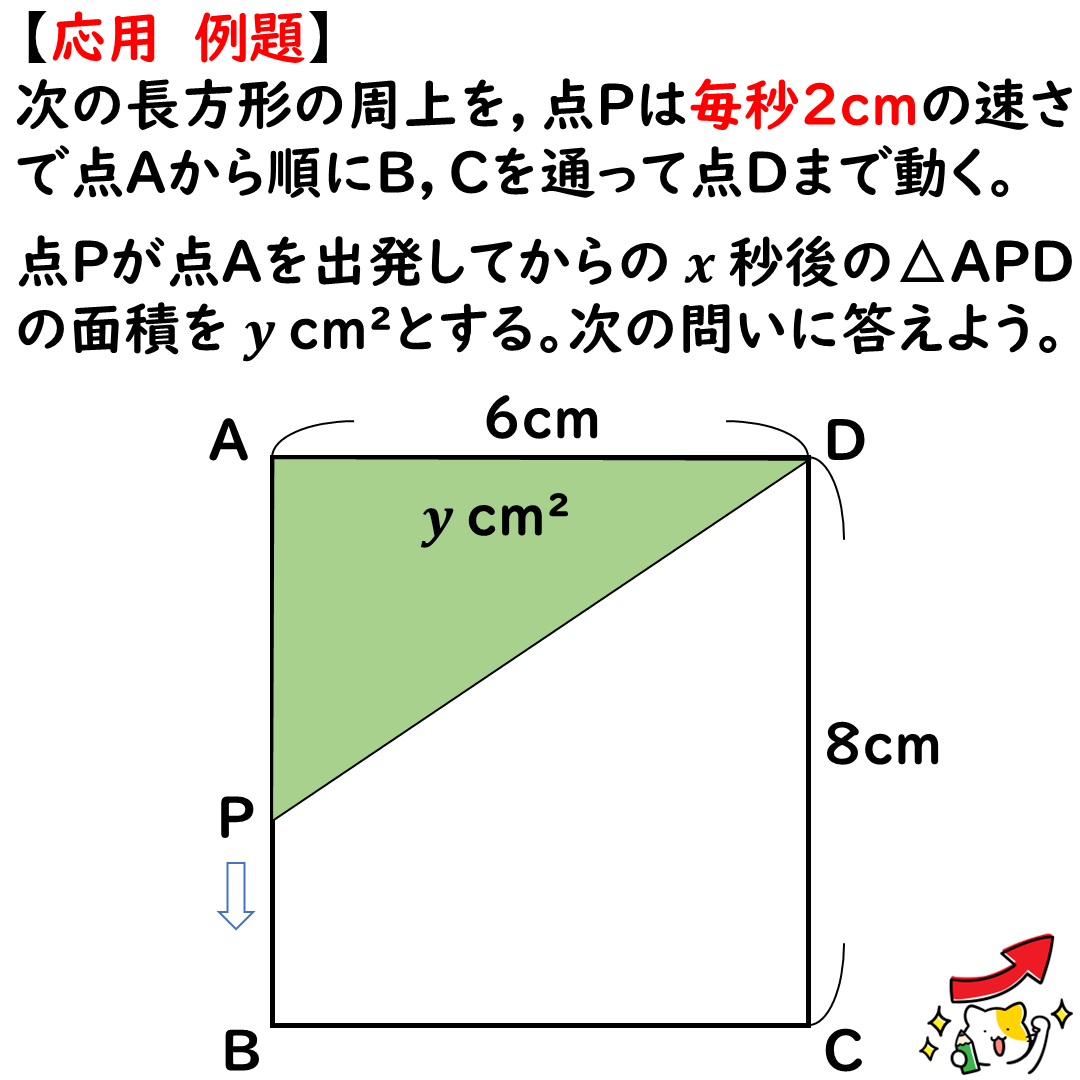
【発展】点Pが毎秒2cmで動いたら。
応用例題を1つ出します。
答えは,ご自身で出してみてください。
数字1個しか変えてないけど,
それだけでちょっぴり難しくなる。


答えがわかった生徒さん,
答えを知りたい生徒さん,
公式ラインから連絡してね。
以上,
動く点Pと面積の変化の
問題特集でした!


コメントはこちらからどうぞ☆