【都立入試そっくり①-2】2次関数

都立の高校入試向けの

問題を制作して授業もしたので

その記録を公開いたします。

都立入試の過去問を参考にして

問題制作しています。

ぜひチャレンジしてみてください！

2次関数にチャレンジだ！

（１）は変域の問題。

（２）の①は一次関数の式，

②は面積を求める問題です。

ぜひチャレンジしてみてください。

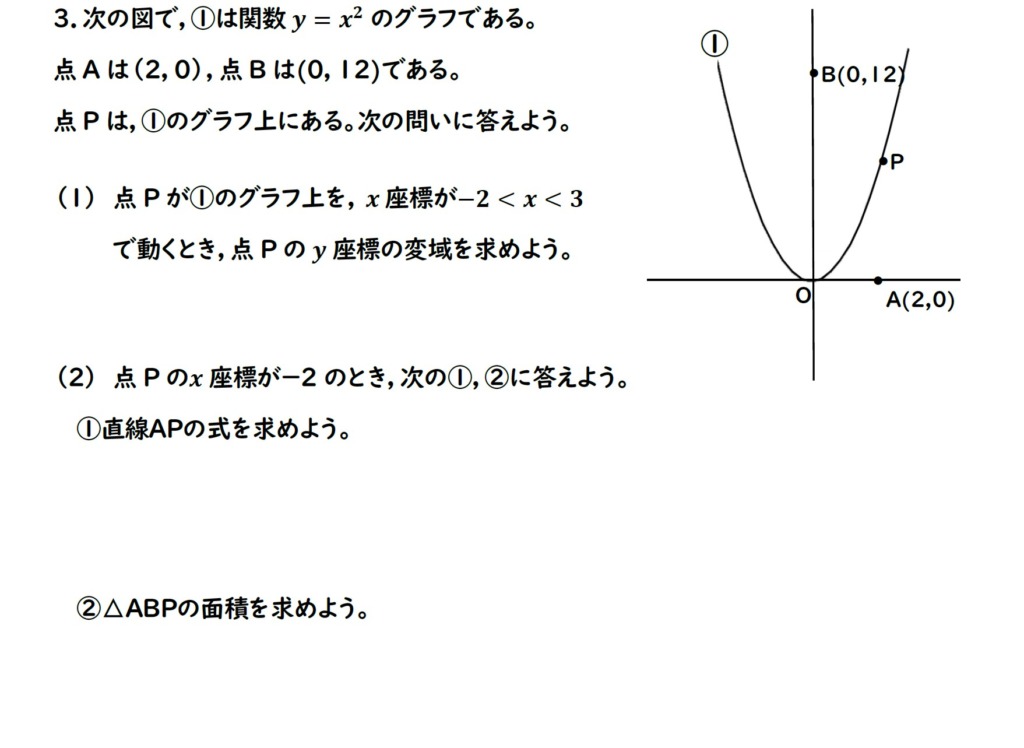
正解は下にあります。

動画で解説授業もしています。

ぜひご覧ください。

解説動画で一緒に学ぼう。

中3生と授業した時の録画です。

キミも一緒に学ぼう！

こたえと解説

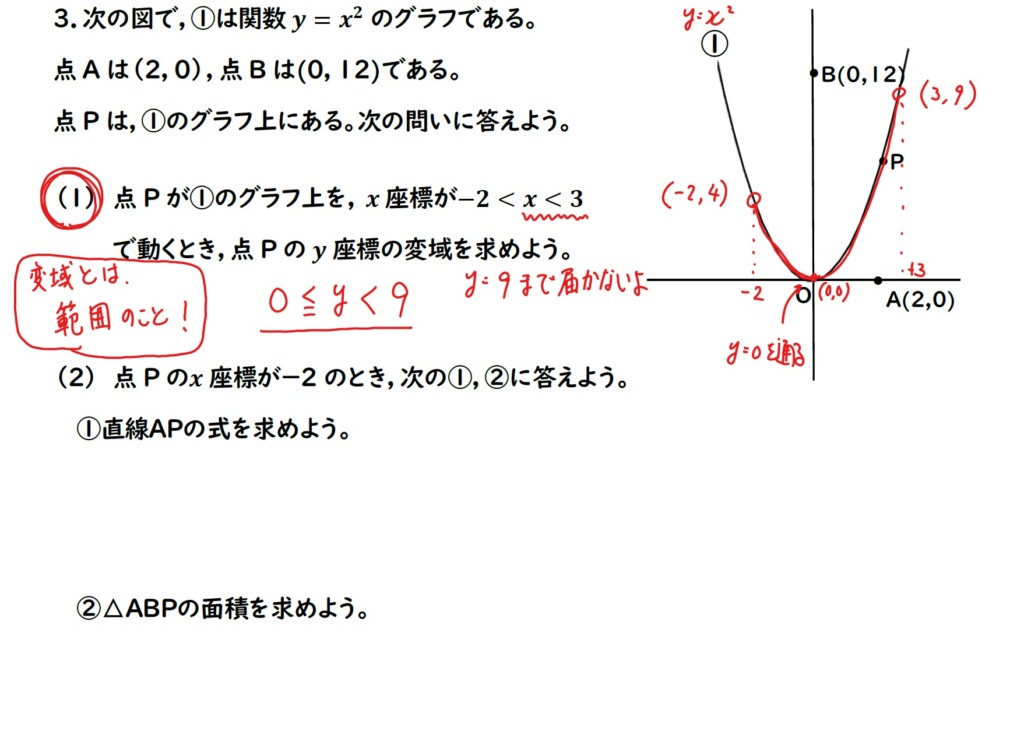
（１）　０≦ｙ＜９

ｙの変域は０以上，9未満です。

９は入らないよ！

ー２＜ｘ＜３だから

ｘ＝３まで行かないよ！

変域とは，範囲のことです。

ココからココまで。

最小値　＜　ｙ　＜　最大値

みたいに囲んで表現します。

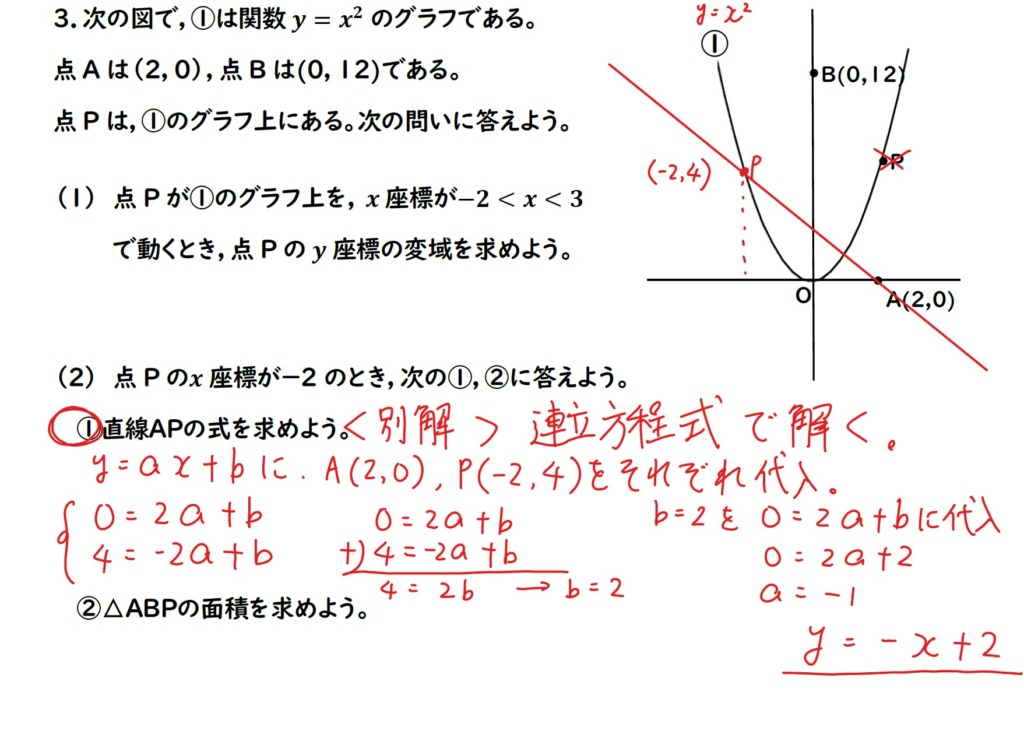
（２）①　ｙ＝－ｘ＋２

2次関数の問題あるある！

一次関数の式を求めさせる問題。

求め方として，次の2種類があります。

①　変化の割合を使う方法

②　連立方程式を使う方法

お好みの方法を使って下さい。

両方解説しています。

ちなみに，

私は変化の割合を使う方法が好きです。

①　変化の割合で求める方法

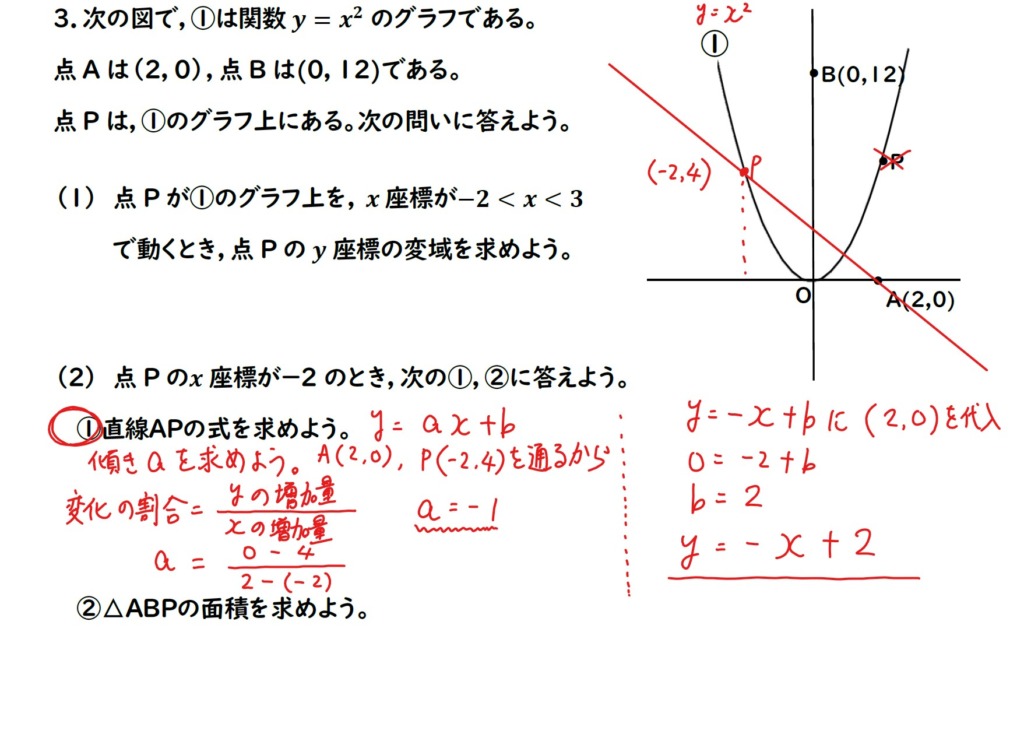
②　連立方程式で求める方法

ｙ＝ａｘ＋ｂに座標を代入していきます。

（２）②　２０

都立入試に限らず，

2次関数では面積を求める問題は

本当によく出ます。

一気に求めるやり方もありますが，

大抵は２つにわけて解く方法が

オススメです。

まず，△ＡＢＰを確認しよう！

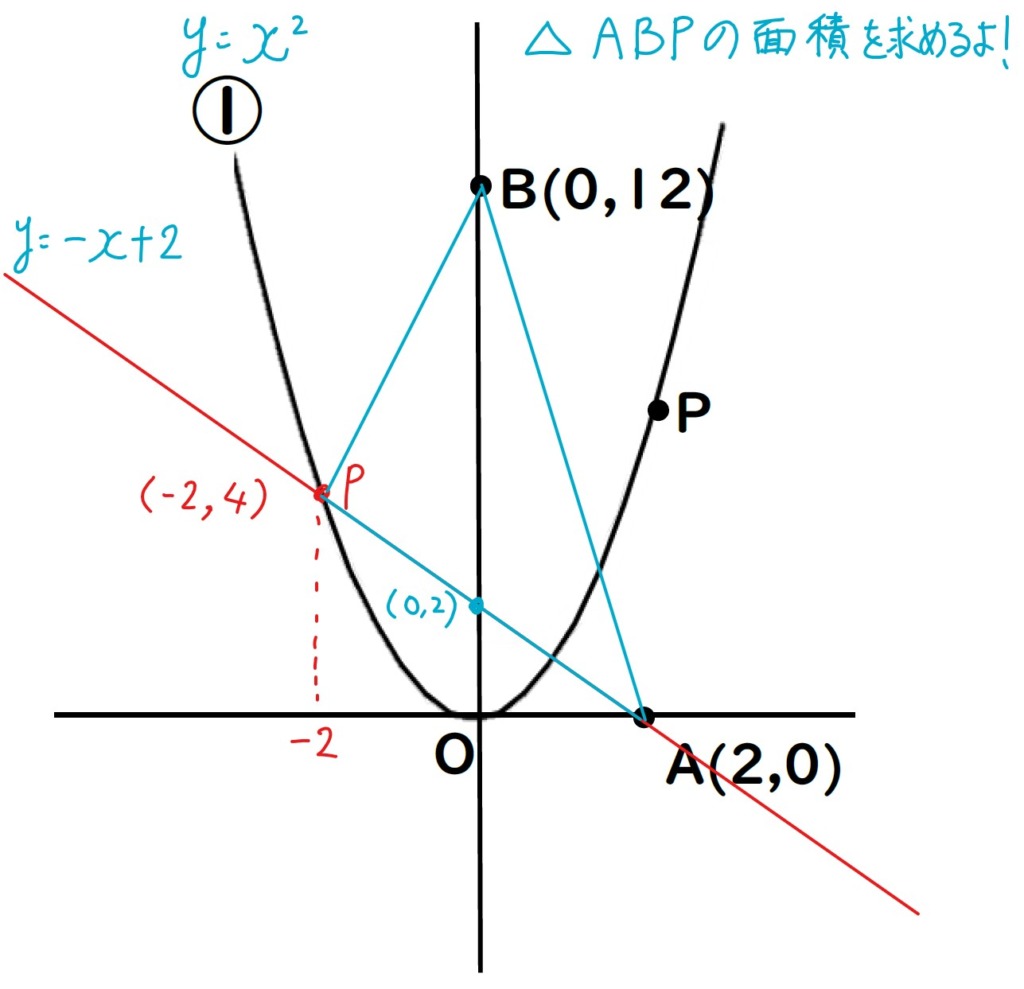
次に，

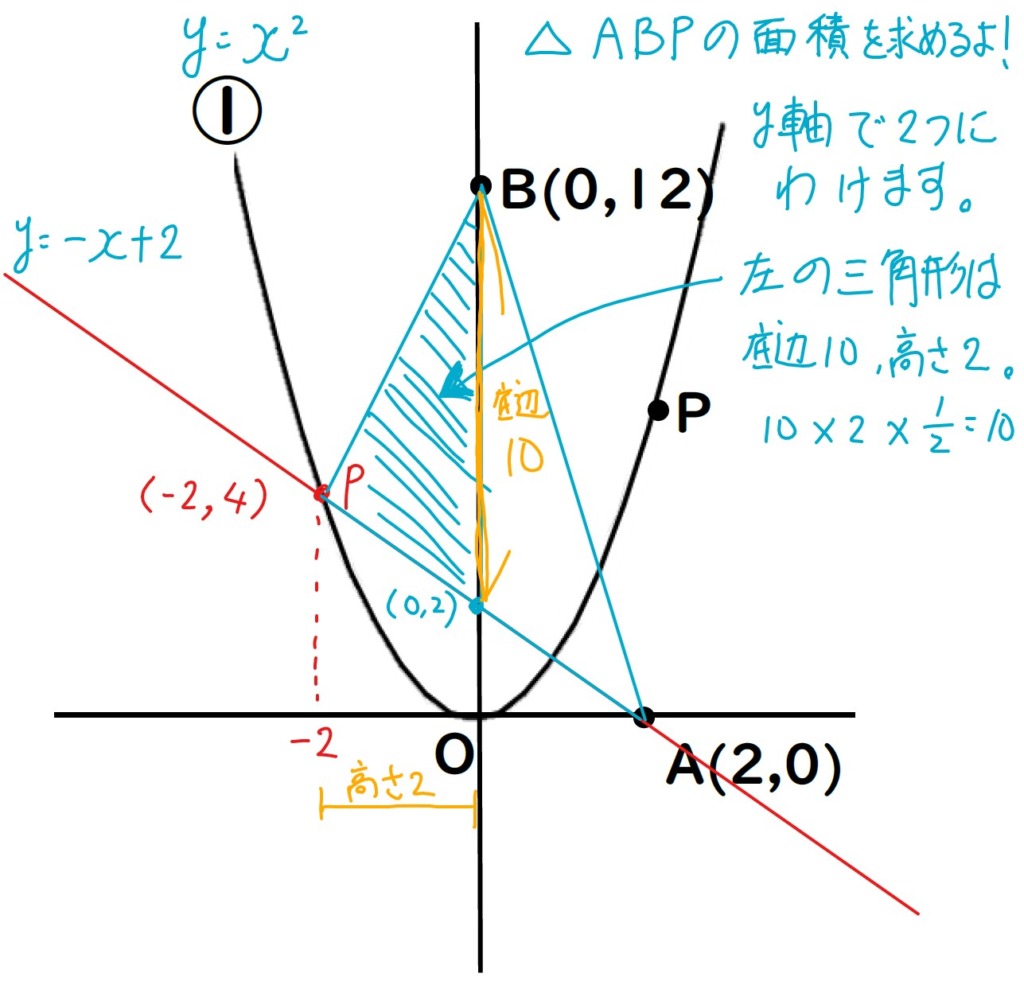
△ＡＢＰをｙ軸で２つに分けます。

直線ＡＰの切片が（０，２）だから

左の三角形の底辺は１０になる。

高さはｐのｘ座標の絶対値の２。

１０　×　２　÷　２　＝１０

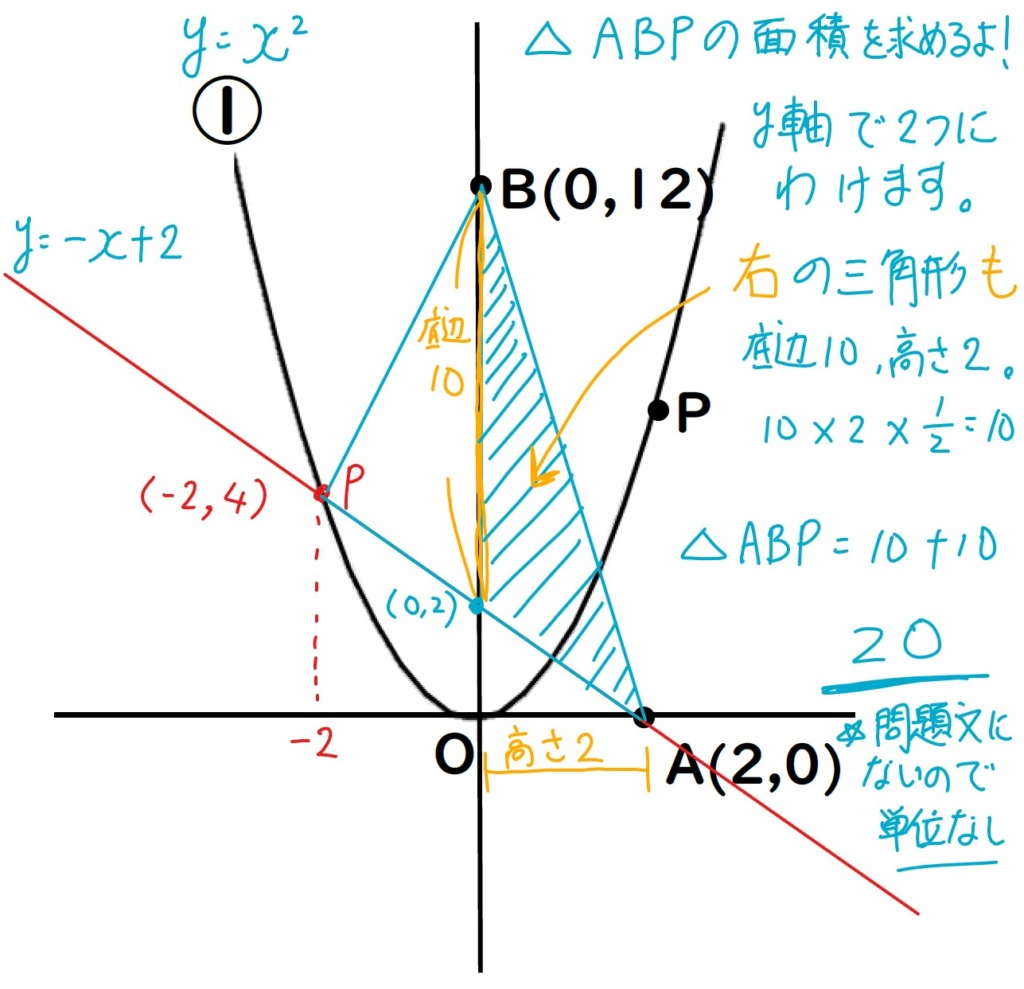
次は，右側の△ＡＢＰの面積も

求めよう。

同様に，底辺１０，

高さは点Ａのｘ座標の絶対値２。

１０　×　２　÷　２　＝１０

△ＡＢＰ＝１０＋１０＝２０

問題文には単位について

書いてないから単位なし。

今回の都立入試そっくり問題は

以上です。

簡単だったでしょうか，

難しかったでしょうか。

都立入試は

問題量で攻めてくるタイプですから

速く正確に！

が求められます。

これからも鍛えていこう！

問題チャレンジした生徒さんへ！

「都立入試対策，やってみたよ！」

と感想やコメントいただけますと

うれしいです！