8/31まで，夏の勉強会イベント開催☆
限定３名様☆
オンライン秘密特訓で
逆転したい生徒さん，集まれ！
「もうどうしたらいいの！？」
そんなキミこそチャンスだ！
保護者の方からお申込みください。
例題にチャレンジだ！
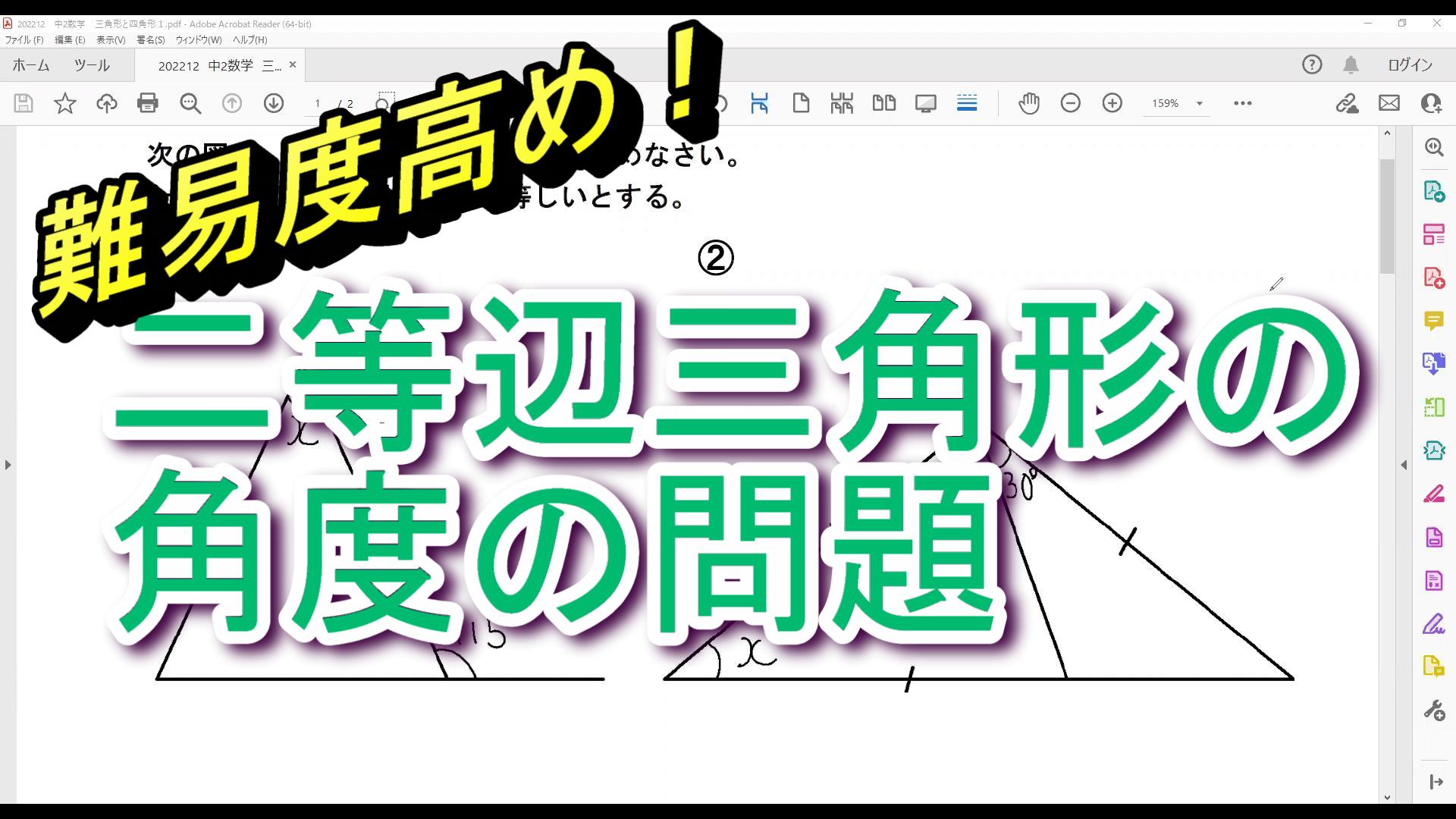
例題）
次の図で，ＢＥ＝ＣＤ，∠ＢＥＣ＝∠ＣＤＢ=90°のとき，
△ＡＢＣは二等辺三角形であることを証明しなさい。
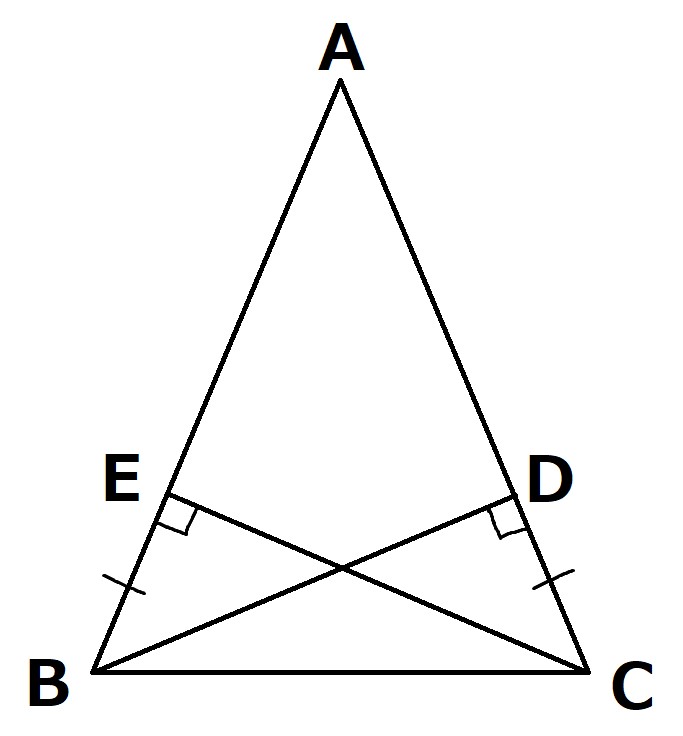
直角三角形なのか二等辺三角形なのか，どっちをどうやればいいのか。
そんな問題です。
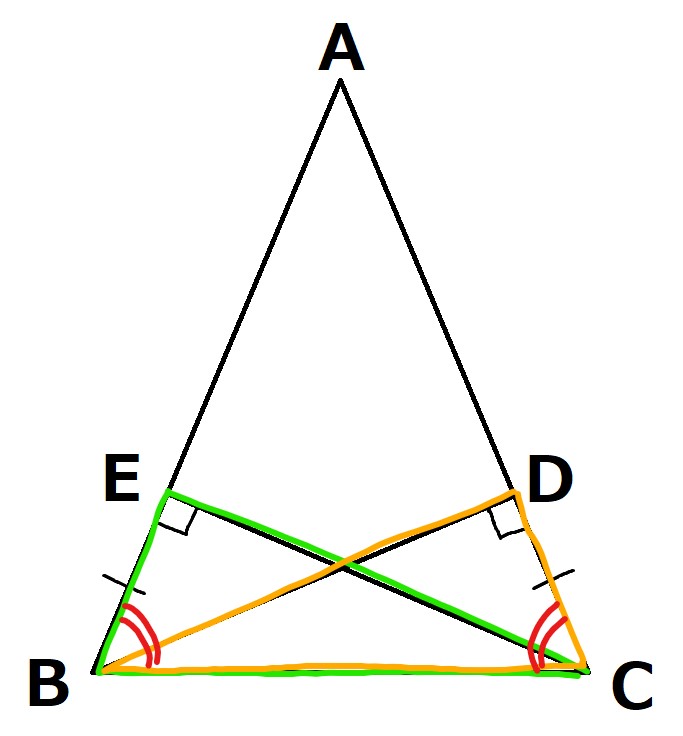
流れとしては，直角三角形の合同を証明して，底角が等しいことを証明して
△ＡＢＣが二等辺三角形であることを示します。
オンライン授業動画で一緒に学んでいこう！
生徒さんも参加しているオンライン授業動画です。ぜひ視聴しながら進めてみてください。
解答・解説はこちらから
まずは，直角三角形である，△ＥＢＣと△ＤＣＢに注目して合同を証明していきます。
合同が証明できれば，対応する角も等しいので，大きな三角形ＡＢＣの底角が等しいことがわかります。
△ＡＢＣは二等辺三角形だと示すことができます。
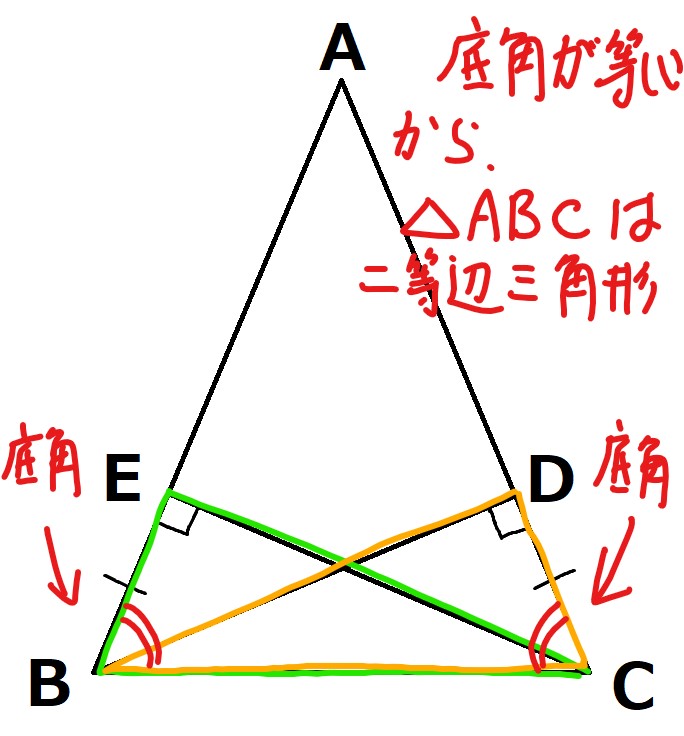
証明の流れ）
△ＥＢＣと△ＤＣＢにおいて，
仮定より，
ＢＥ＝ＣＤ・・・①
∠ＢＥＣ＝∠ＣＤＢ＝90°・・・②
共通な辺だから，
ＢＣ＝ＣＢ・・・③
①，②，③より
直角三角形の，斜辺と他の1辺がそれぞれ等しいので，
△ＥＢＣ≡△ＤＣＢ
合同な図形の対応する角は等しいので，
∠ＥＢＣ＝∠ＤＣＢ
底角が等しいので，△ＡＢＣは二等辺三角形である。
レビューの平均
4.4
5つ星中4.4つ星です！（197人のお客様のデータ）
最高71%
良かった14%
ふつう4%
いまいち3%
最悪8%
お客様の声
GOOD
英語
アスミラからの返信
コメントありがとうございます。
夏休みも頑張っていますね！
分かった
ｌ
アスミラからの返信
んん？
夏休みも勉強がんばろう！
とても実用性がある問題
詳しく解説したり、分かりやすくしてくれていたから、とても良かった！
大須賀信夫
アスミラからの返信
コメントありがとうございます。
これからもぜひご活用ください！
すごくよかった
Nice君
アスミラからの返信
コメントありがとうございます，夏休みも楽しく続けてね！
いい問題です！
やり方までしっかりと記されてますので
とても分かり易かったです( ´∀｀)
ありがとうございます。
二郎
最高すぎるて🫶🏻
ずっとわからなかったやつがわかりました🥹💗
偏差値70目指して頑張ります！！！
あまま
アスミラからの返信
コメントありがとうございます。勉強がんばってくれい。
説明詳しー!！
説明がめっちゃ詳しくて、これからも参考にして行こうと思いまーす❣️
苦手な理科も少しずつ克服していきまーす！
勉強頑張るぞー
住宅渋谷
アスミラからの返信
思わず応援したくなるコメントだ！
理解できスギィ
理科が苦手な自分にとっては最高だってはっきりわかんだね。
もっと理科の問題を発信してほしいゾー
364364
アスミラからの返信
理科かあー，リクエストありがとうございます。
わかりやすい！！
自分は社会がすごく苦手だけど、
わかりやすくまとめられているので、
とてもわかりやすいです！
これからも、このサイトを使って勉強したいです！！
実力テストがんばります！！
Ａ
アスミラからの返信
コメントありがとうございます。
社会のテスト対策って難しいけど，楽しくやった者勝ちなところあるから応援してます。
やばい
あ
アスミラからの返信
説明が下手で申し訳ないです…。
できれば，どの問題だったか教えていただけないでしょうか・・・。
