7/21(月)までの限定３名様☆
夏期講習の体験会やってます！
オンライン秘密特訓で
逆転したい生徒さん，集まれ！
「もうどうしたらいいの！？」
そんなキミこそチャンスだ！
保護者の方からお申込みください。
直線で囲まれた部分の面積を求めてみよう！
オンライン個別授業動画です，ぜひ視聴してみてください。
今回は後編になります。
前編はこちら。
＜ 問題 ＞
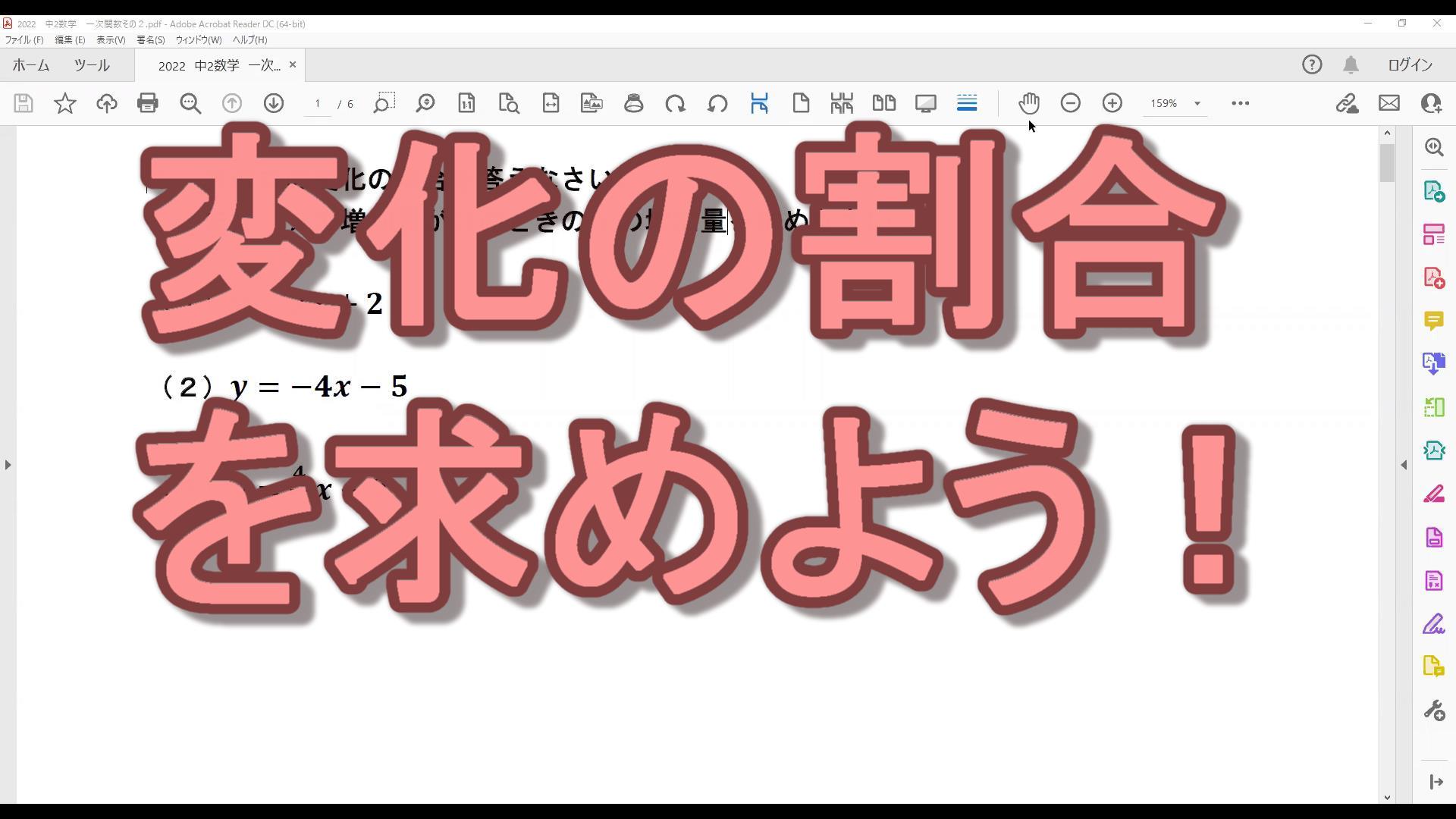
次の図で，直線ｍ，直線ℓ，ｙ軸に囲まれた部分の面積を求めなさい。
座標の1メモリを1㎝とする。
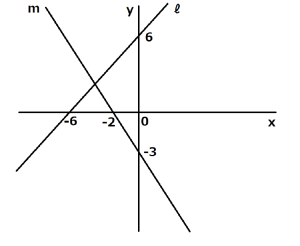
正解はこちら！
前編の動画で，直線ｍと直線ℓの式と，2直線の交点の座標は求めていますので，続きからです。
求めたい部分の面積はこちらです。三角形ですね。
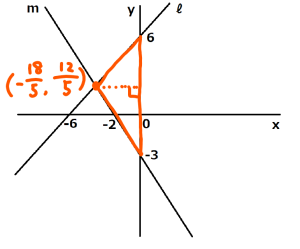
三角形の面積は，底辺×高さ÷２で求められます。
底辺はy軸から求められます。６＋３で９ですね。３は絶対値を使います。
高さですが，直線ｍと直線ℓの交点のｘ座標を使います。絶対値を取って\(\displaystyle \frac{18}{5}\) です。
ですので，
三角形の面積＝\(\displaystyle 9×\frac{18}{5}×\frac{1}{2}=\frac{81}{5}\)
こたえ \(\displaystyle \frac{81}{5}cm^2\)
になります。
レビューの平均
4.4
5つ星中4.4つ星です！（192人のお客様のデータ）
最高71%
良かった14%
ふつう4%
いまいち3%
最悪8%
お客様の声
最高すぎるて🫶🏻
ずっとわからなかったやつがわかりました🥹💗
偏差値70目指して頑張ります！！！
あまま
アスミラからの返信
コメントありがとうございます。勉強がんばってくれい。
説明詳しー!！
説明がめっちゃ詳しくて、これからも参考にして行こうと思いまーす❣️
苦手な理科も少しずつ克服していきまーす！
勉強頑張るぞー
住宅渋谷
アスミラからの返信
思わず応援したくなるコメントだ！
理解できスギィ
理科が苦手な自分にとっては最高だってはっきりわかんだね。
もっと理科の問題を発信してほしいゾー
364364
アスミラからの返信
理科かあー，リクエストありがとうございます。
わかりやすい！！
自分は社会がすごく苦手だけど、
わかりやすくまとめられているので、
とてもわかりやすいです！
これからも、このサイトを使って勉強したいです！！
実力テストがんばります！！
Ａ
アスミラからの返信
コメントありがとうございます。
社会のテスト対策って難しいけど，楽しくやった者勝ちなところあるから応援してます。
やばい
あ
アスミラからの返信
説明が下手で申し訳ないです…。
できれば，どの問題だったか教えていただけないでしょうか・・・。
意外といけた
アタオカ
アスミラからの返信
コメントありがとうございます。
これからも自信をもって取り組んでくれい！
わかりやすい解説
めっっっっちゃ
わかりやすいｯｯｯｯ
テスト頑張りやす。
スマイル君
アスミラからの返信
コメントありがとうございます。
1学期期末テストかな，がんばれ！
よかった
問題も比較的解きやすかった。
苦手が克服できそうかも…？
lonelylonely
アスミラからの返信
誰にでも苦手はあるので，無理に克服しなくても良いかと。
苦手にチャレンジできること自体がすごい！
頑張ってできた！
難しかったけどなんとか解けましたー！
テスト頑張る！
まろ
アスミラからの返信
何やらすごい意欲を感じるコメントだ！
応援しています！
Very good
あひるの子
アスミラからの返信
コメントありがとうございます。
私のオンライン個別指導もぜひご検討くださーい。
