応用編！　式による証明にチャレンジしてみよう！３　後半

応用編！式による証明にチャレンジ！３　後半

 

 

 

次の問題にチャレンジしてみよう！

 

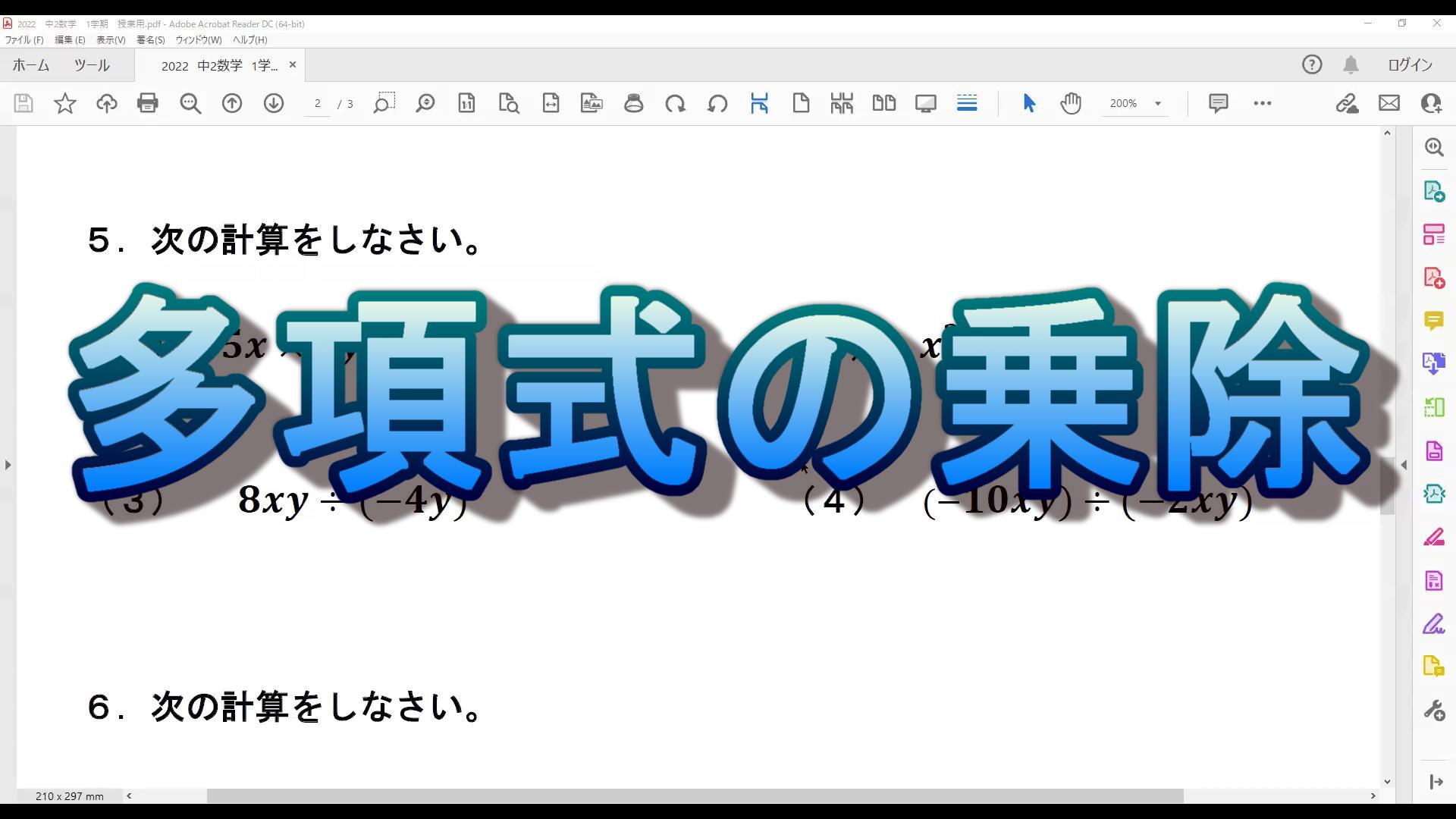
＜問題＞

2けたの自然数と，その数の一の位の数と十の位の数を入れかえた数の差は，9の倍数になることを説明しなさい。

 

次の（　　　）に式を入れていこう！

 

＜説明＞

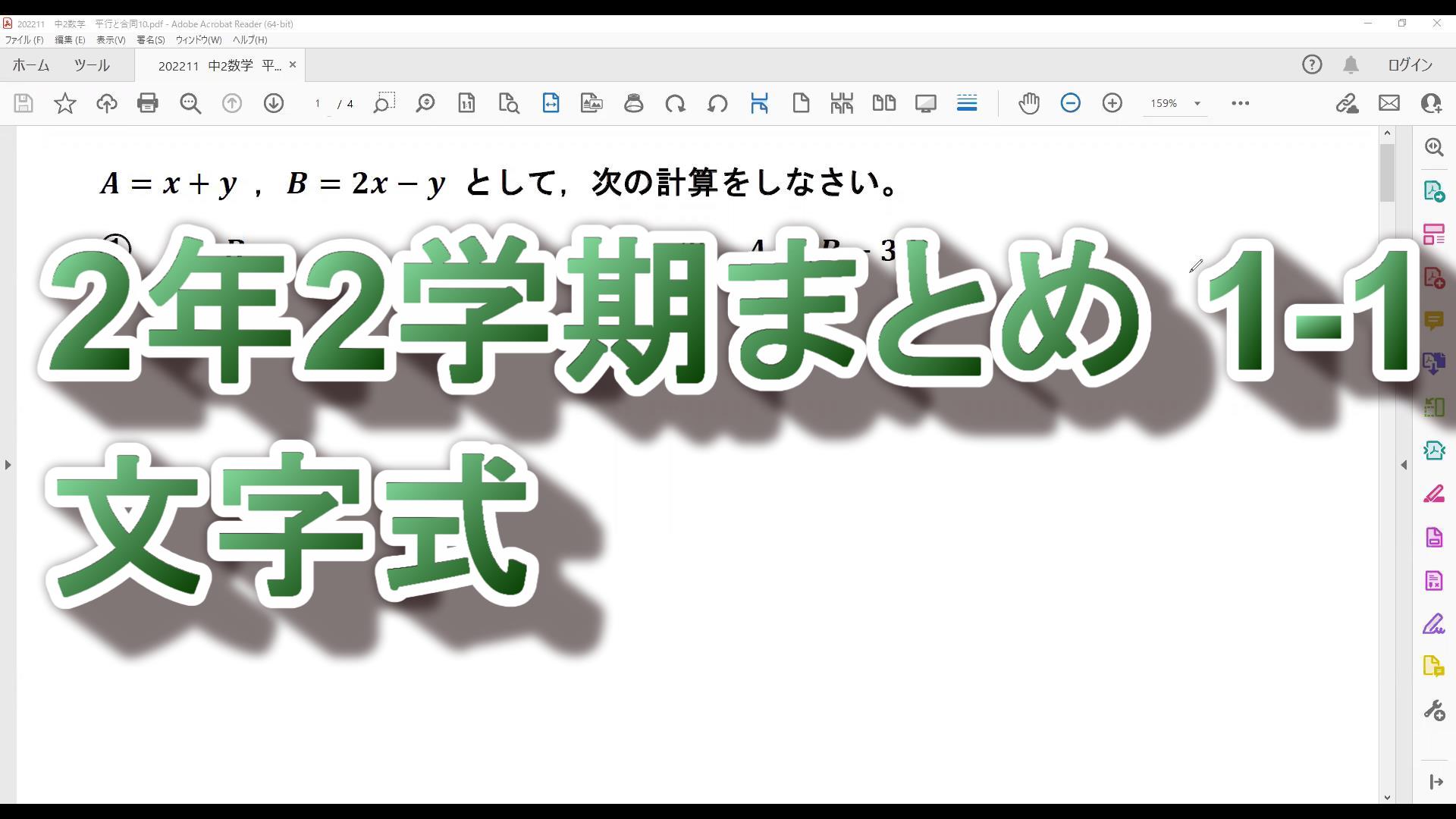
はじめに考えた数の十の位を\(x\)，一の位を\(y\)とすると

はじめの数は（　　　　　）

入れかえた数は（　　　　　）

と表される。

 

したがって，それらの差は

（　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　）

 

（　　　　）は整数だから，（　　　　　　）は9の倍数である。

したがって，2けたの自然数と，その数の一の位の数字と十の位の数字を入れかえた数の差は9の倍数になる。

 

 

 

 

 

正解はこちら！

 

＜問題＞

2けたの自然数と，その数の一の位の数と十の位の数を入れかえた数の差は，9の倍数になることを説明しなさい。

 

次の（　　　）に式を入れていこう！

 

＜説明＞

はじめに考えた数の十の位を\(x\)，一の位を\(y\)とすると

はじめの数は（　\(10x+y\)　）

入れかえた数は（　\(10y+x\)　）

と表される。

 

それらの差は

（　　\((10x+y)-(10y+x)=9(x-y)\)　　)

 

（　\(x-y\)　）は整数だから，（　\(9(x-y)\)　）は9の倍数である。

したがって，2けたの自然数と，その数の一の位の数字と十の位の数字を入れかえた数の差は9の倍数になる。

 

 

 

授業動画はこちら！

 

生徒さんとの授業動画です。途中からの動画で切り抜き2分53秒です。

一緒に学習してみてください！