
今回は,中2数学の等積変形を
例題を通して解説します。
等積変形が登場するのは,
大体,中2生の2学期後半かなあ。
三角形の合同証明の学習後あたりです。
等積変形って入試レベルでは
けっこう必須スキルなんですが
教科書ではサラッと学ぶ程度で
終わっちゃうんですよね。
というわけで,
一次関数と等積変形を混ぜて
基本からやっていきます。
中3生の高校入試レベル入門にも
オススメ☆
問題①,②にチャレンジだ☆
簡単な例題を制作しました。
ぜひチャレンジしてみてください。
問題①と②があります。
どちらからでも解けます。
どちらも等積変形を使って解けるよ。
問題②は等積変形は使わなくても
あっさり解けるよ。
答えはすぐ下にあります。

答えは,
① 8
② -12,12
重要なのは,答えじゃない。
解き方だよ。
むしろ,
答えなんてどうでもいいぞ。
簡単に解けた方は,
他の応用問題集でも
解いてくれい。
等積変形とは
中2後半で出てくる,
等積変形。
これは,図形の面積そのまま,
変形することだ。

主な使い方としては,
平行線を使ったものだ。
みんなも,図形の問題で
補助線を引くでしょ。
平行線って便利だよね。
三角形の場合,平行線を使えば,
図のように,
底辺と高さを維持したまま
変形ができるのです。
等積変形は,
図形の問題だけでなく,
グラフ問題ととても相性が良い。
入試レベルでは必須スキルになる。
ぜひ身に付けておきたい☆
問題①のヒントと解説
問題①の答えは8だ。
点Pのx座標は8なのだよ。
ここでは,
等積変形のヒントと解説を
出していく。
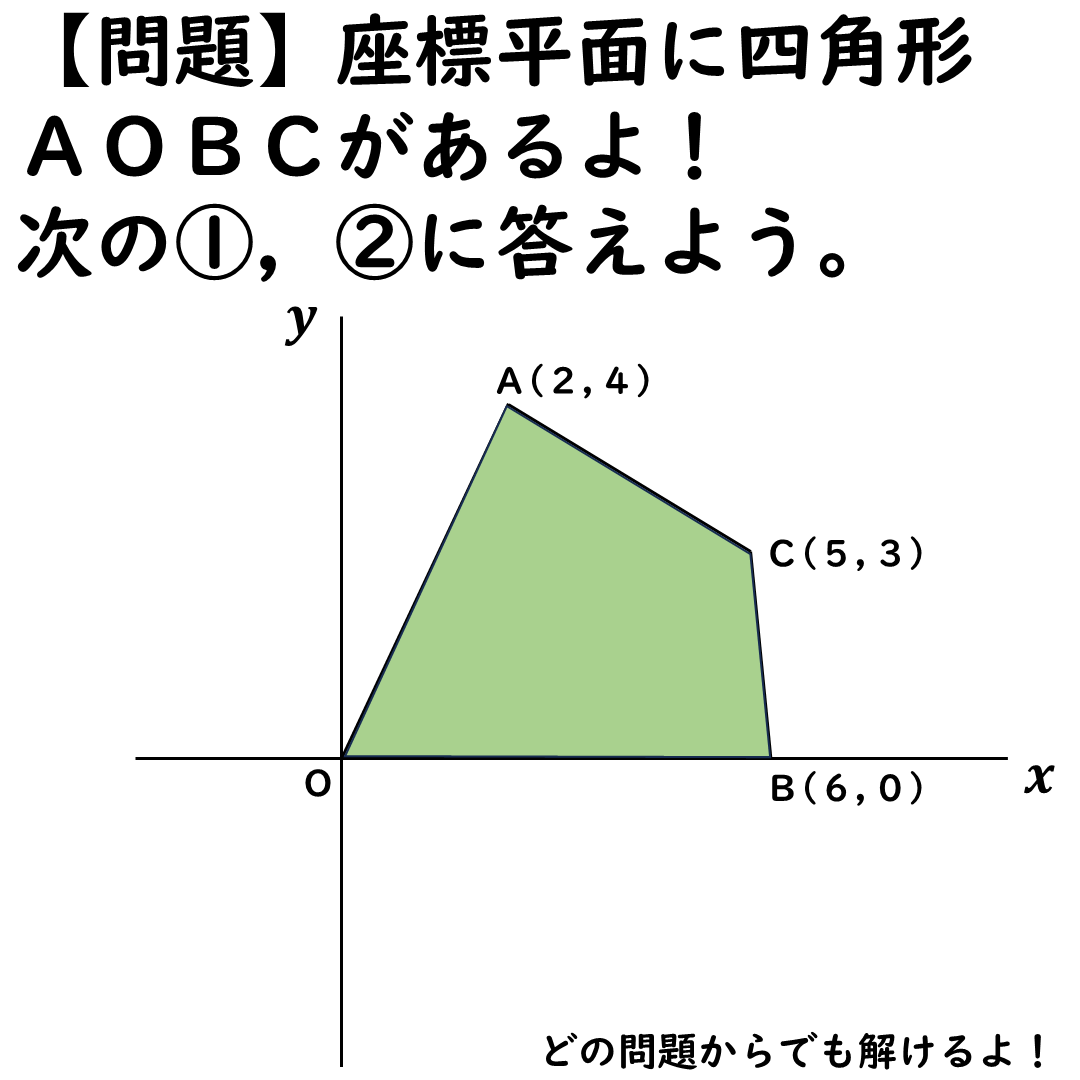
まずは補助線をひく。
点Aと点Bを通る直線だ。
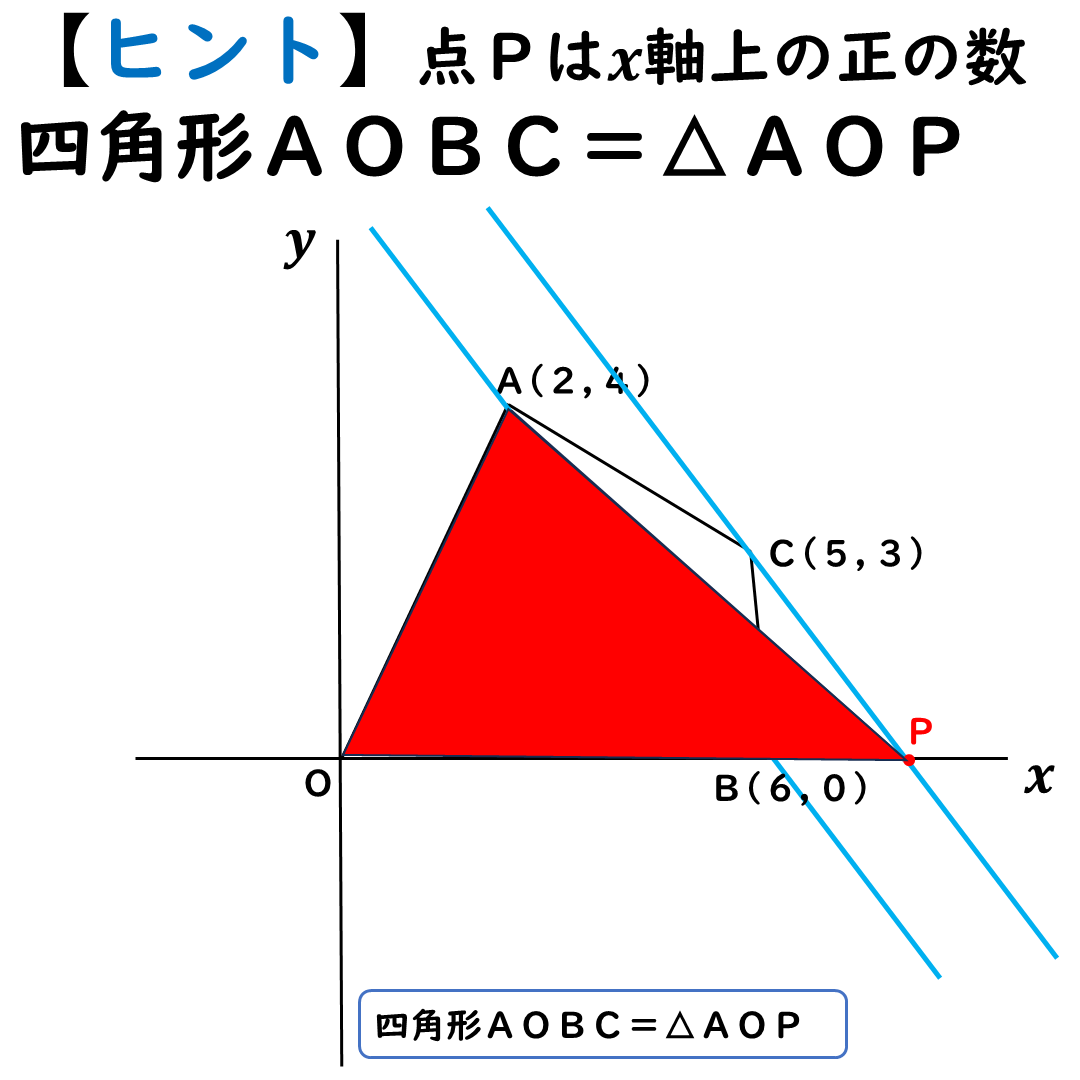
このとき,四角形AOBCは
△AOBと△ABCに分けられる。
今回,等積変形するのは,
△ABCだよ。
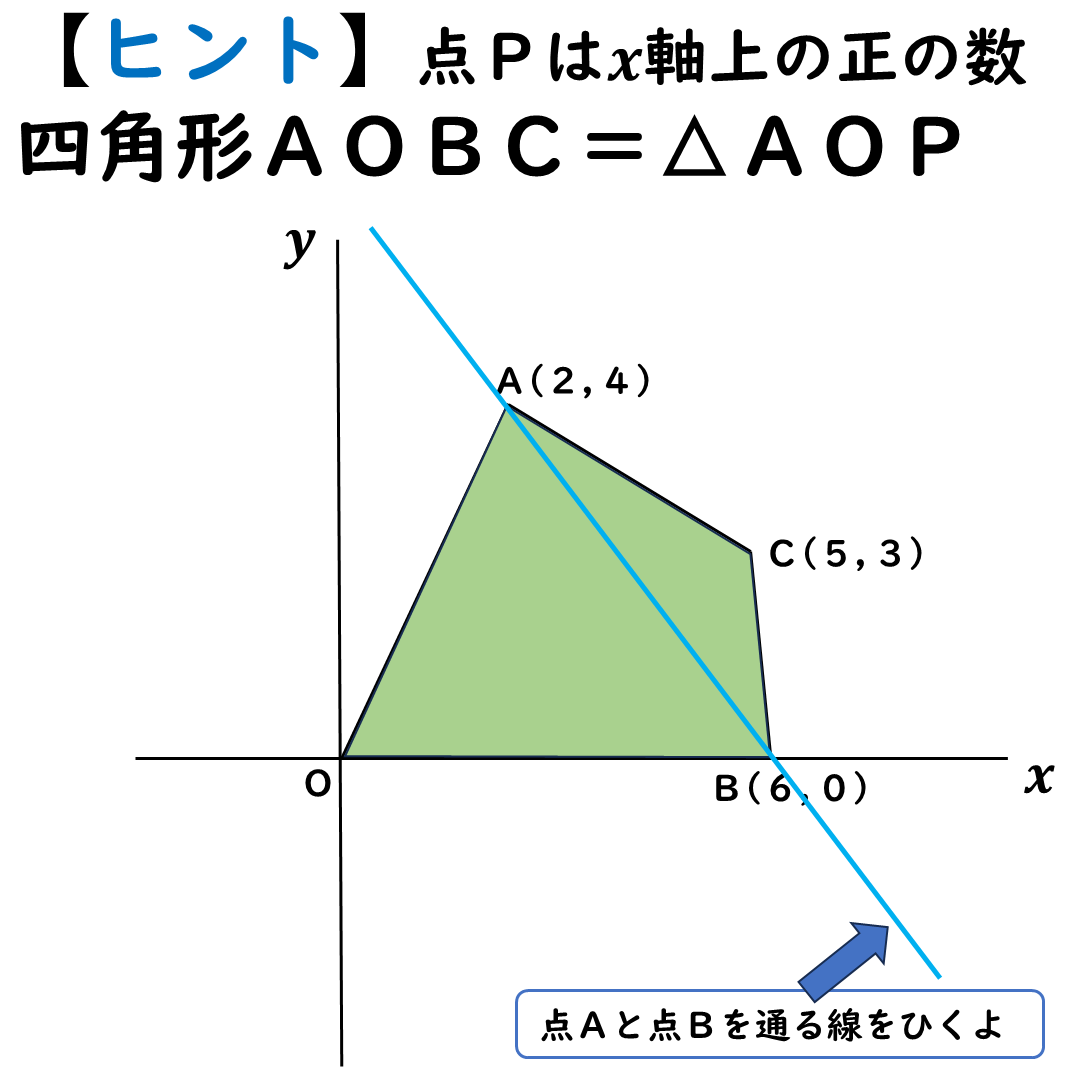
補助線2本目をひく。
点Cを通るような平行線だ。
これから,△ABCを
面積そのまま,変形させていく。
等積変形をしてみよう
等積変形のイメージは
こんな感じ。
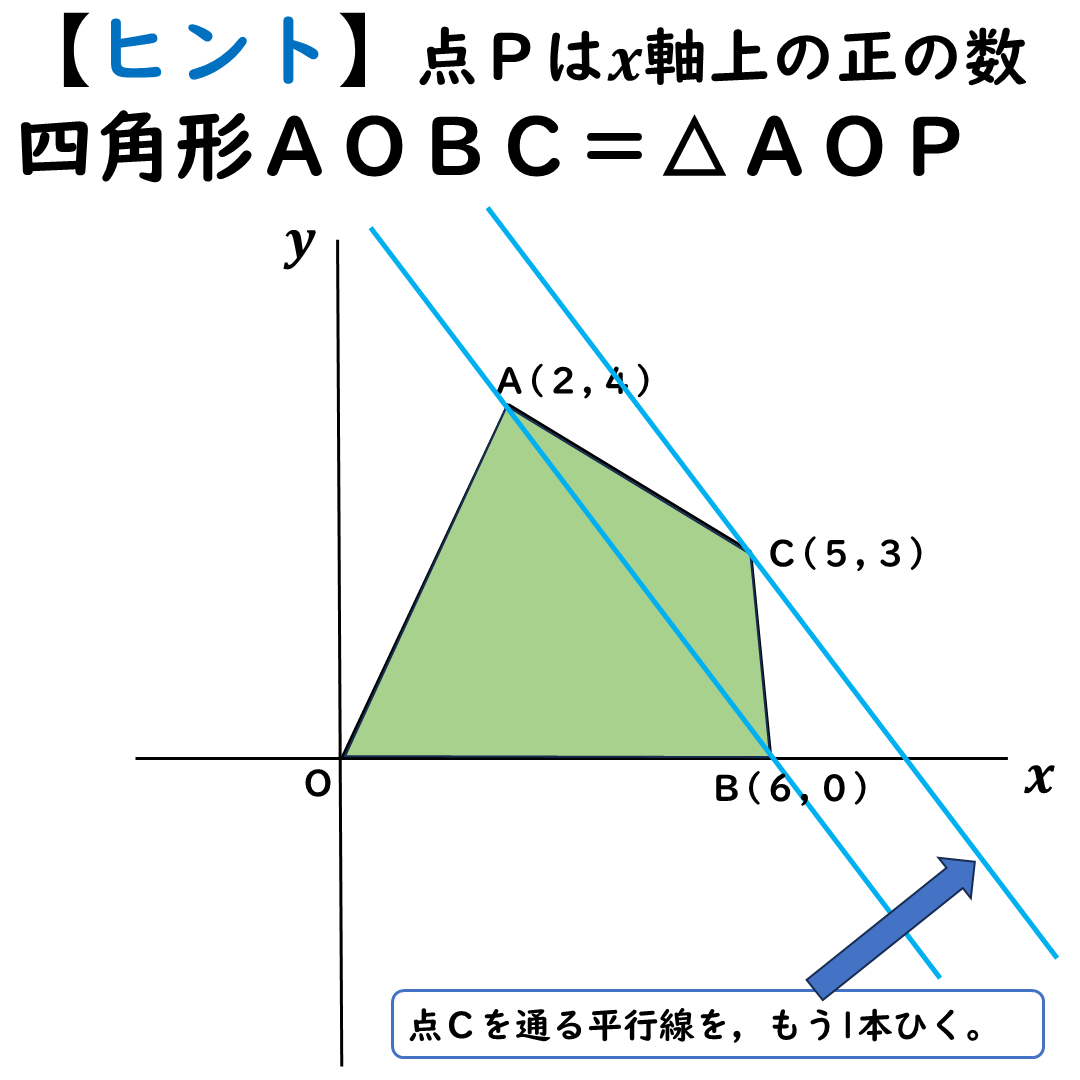
△ABCで,
点Cをx軸まで移動。
そうすれば,
点Cがx軸に交わったところが
点Pになれるよ。
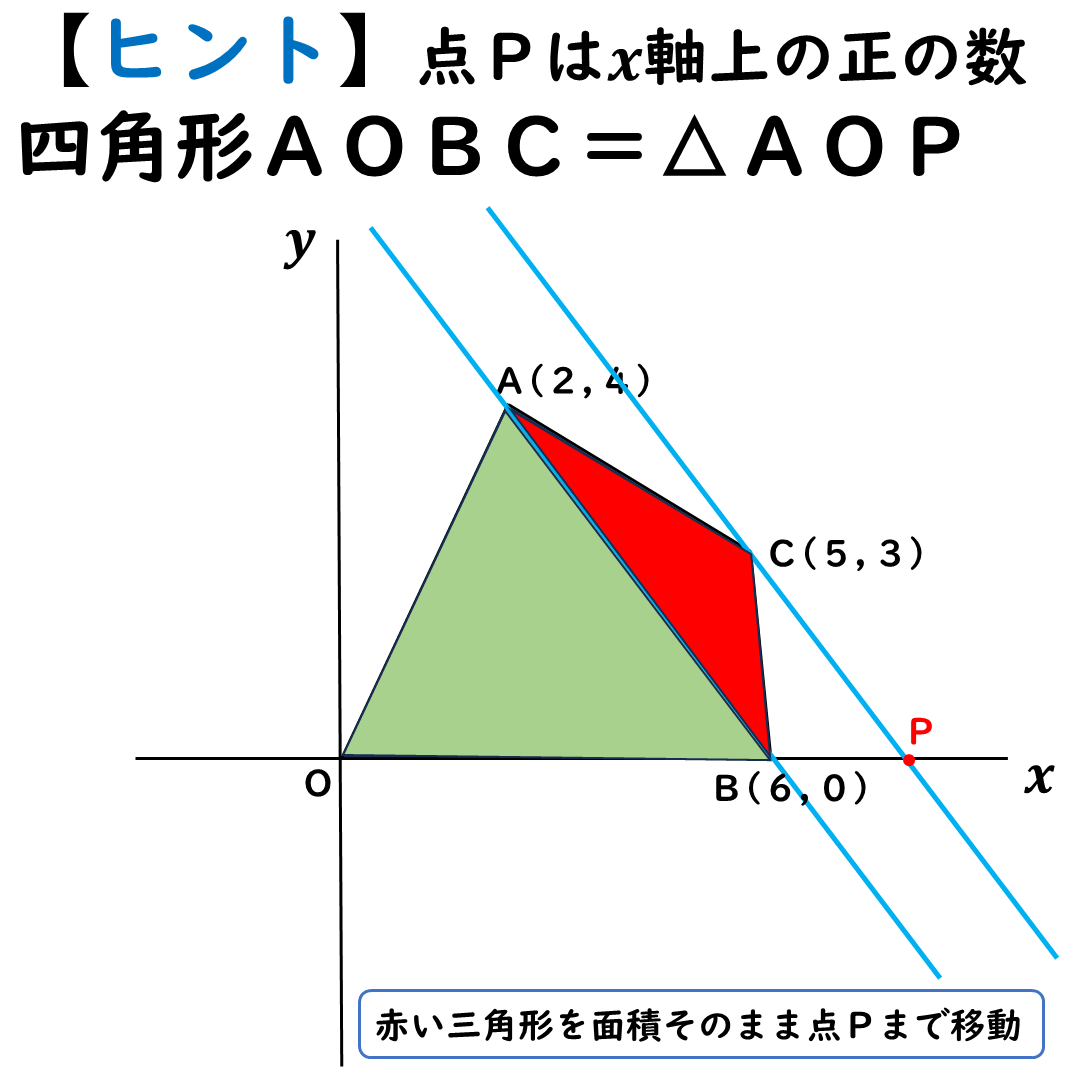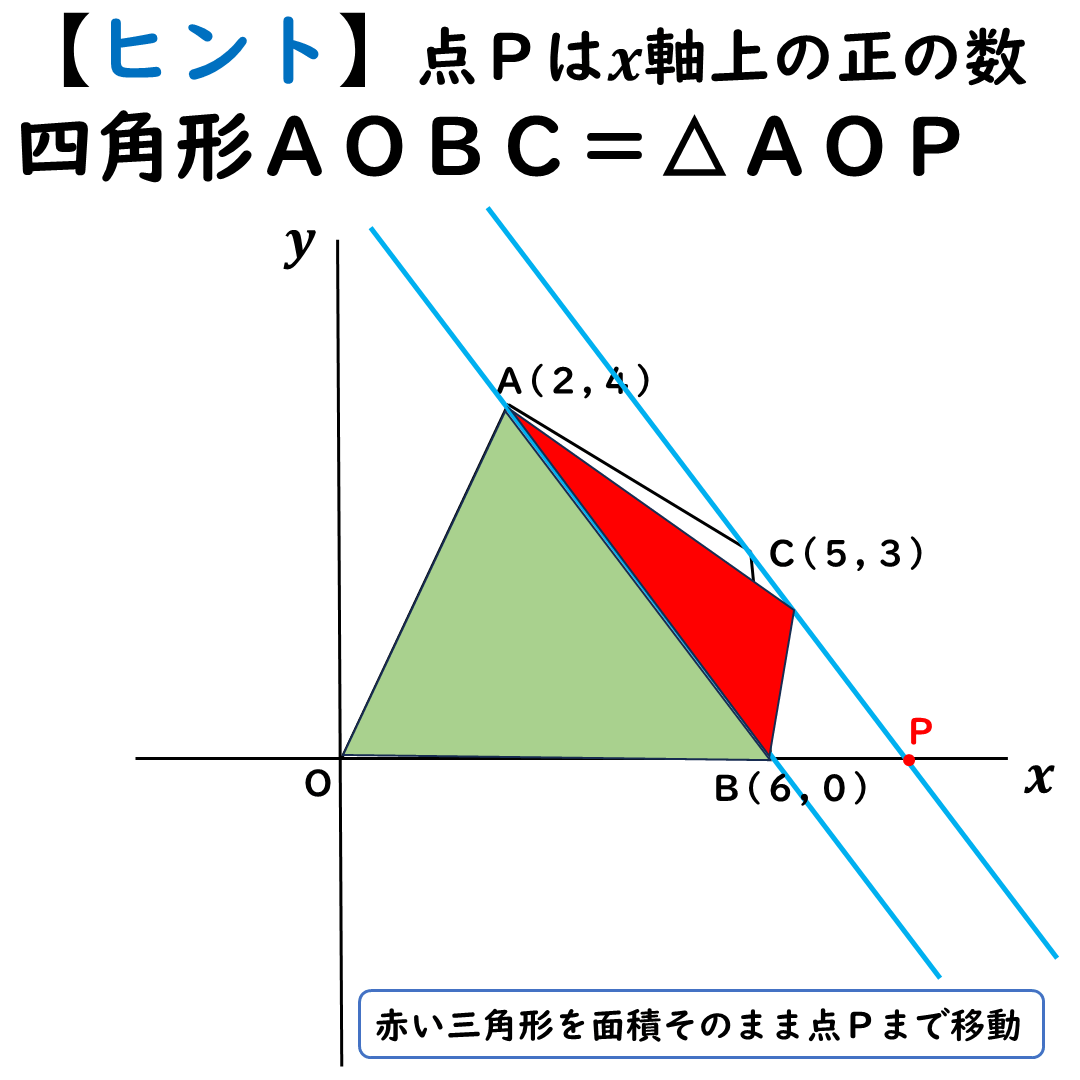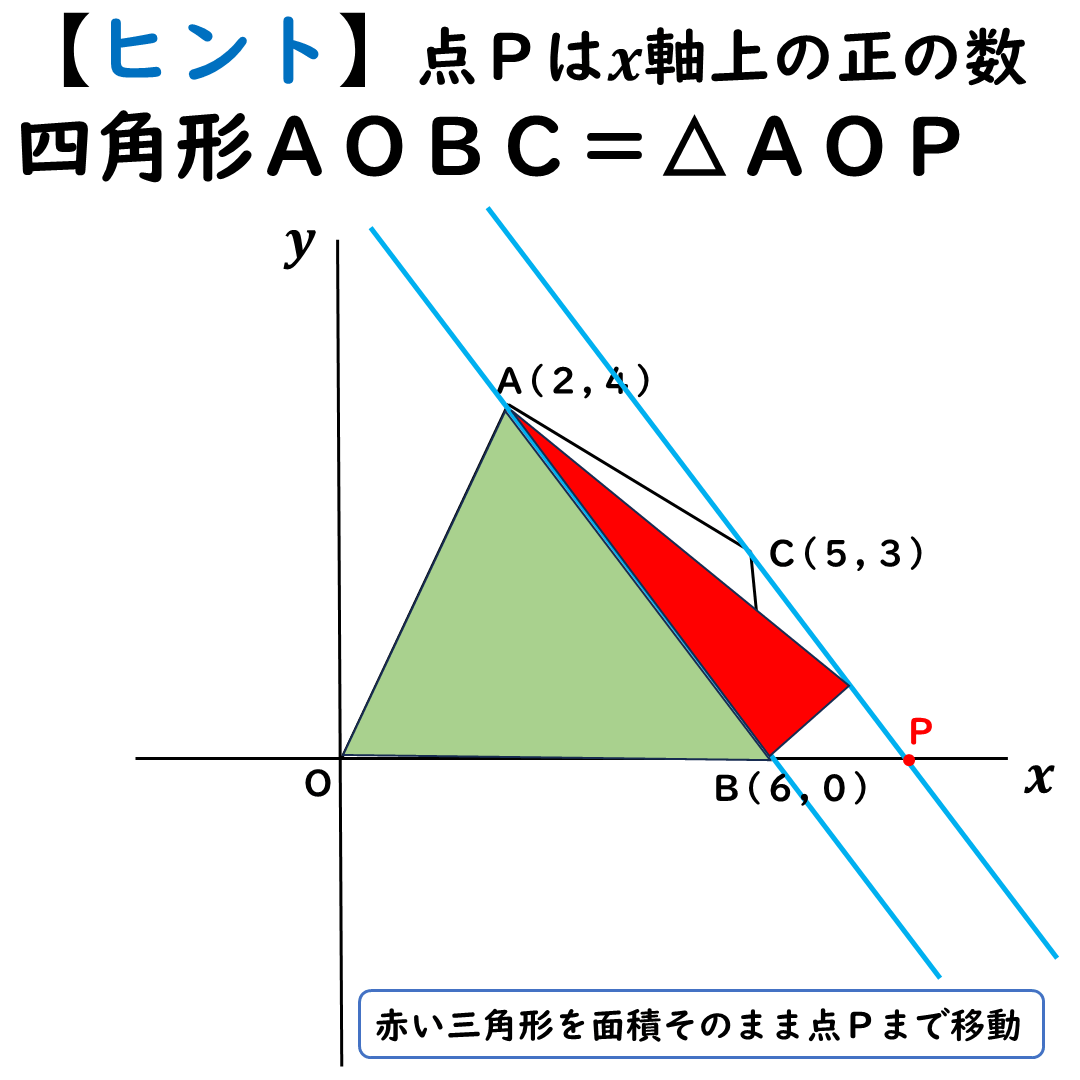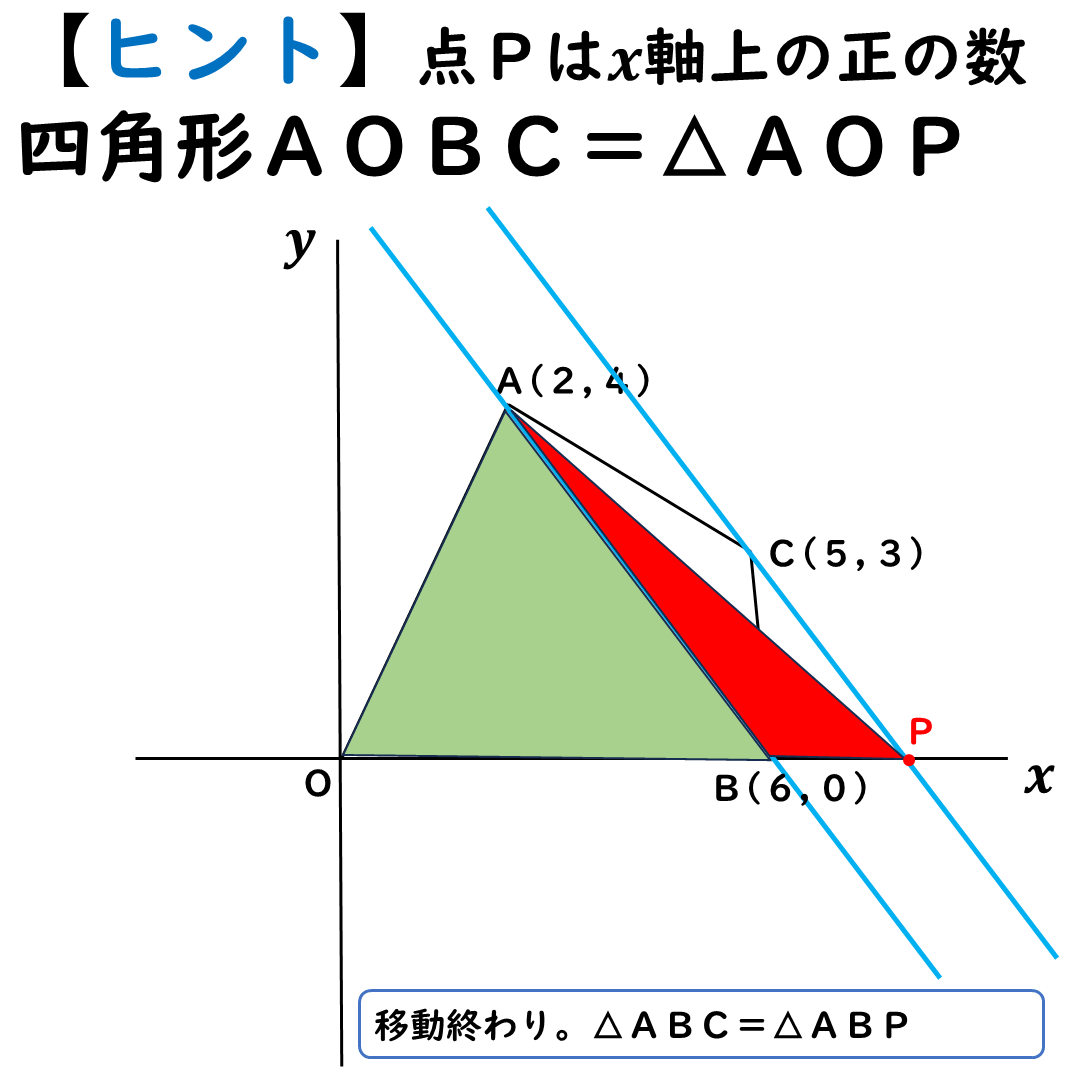
図のように,
点Cをx軸まで移動すれば
四角形AOBC=△AOP
になる。
問題①の解説
あとは,
点Pのx座標を求めよう。
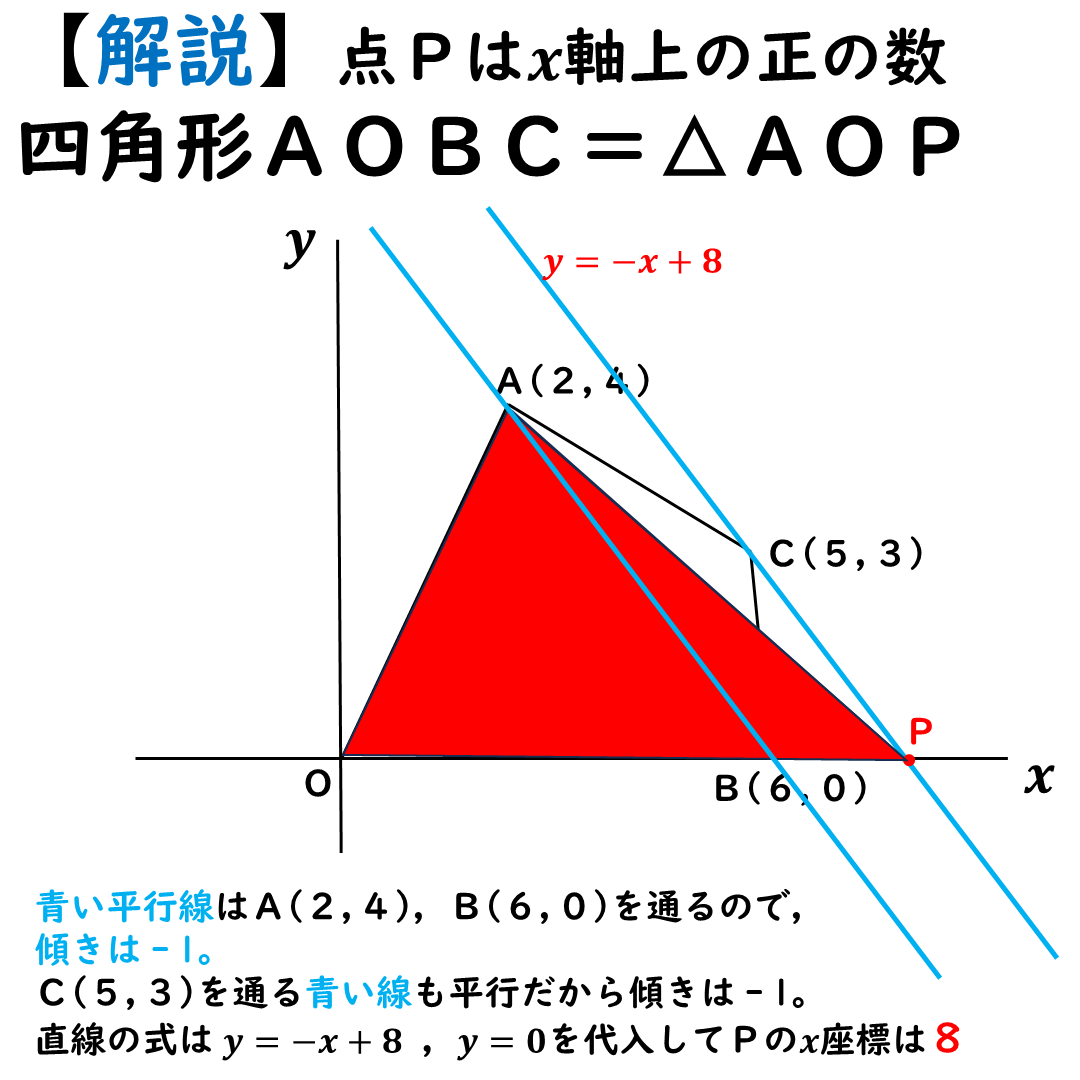
点Pを求めるには,
青い平行線の式を求めればよい。
2本あるけど,
平行線だからどちらも傾きは同じ。
左の平行線は,
A(2,4),B(6,0)を
通るから,
y=ax+bにそれぞれ代入して
連立方程式で求めてもいいし,
xの増加量やyの増加量で
傾き求めるのもいいよね。
傾きはー1と出てくる。
点Pは右の平行線にある。
傾きー1で,C(5,3)を通るので
y=-x+bに代入すればOK。
y=ーx+8と出てくる。
後は,y=0を代入すれば
P(8,0)とわかる。
点Pのx座標は8だ。
問題②のヒントと解説
問題②のこたえは,-12,12だ。
実は,問題②は
等積変形なんて
高級なものは使わず
簡単に解ける。
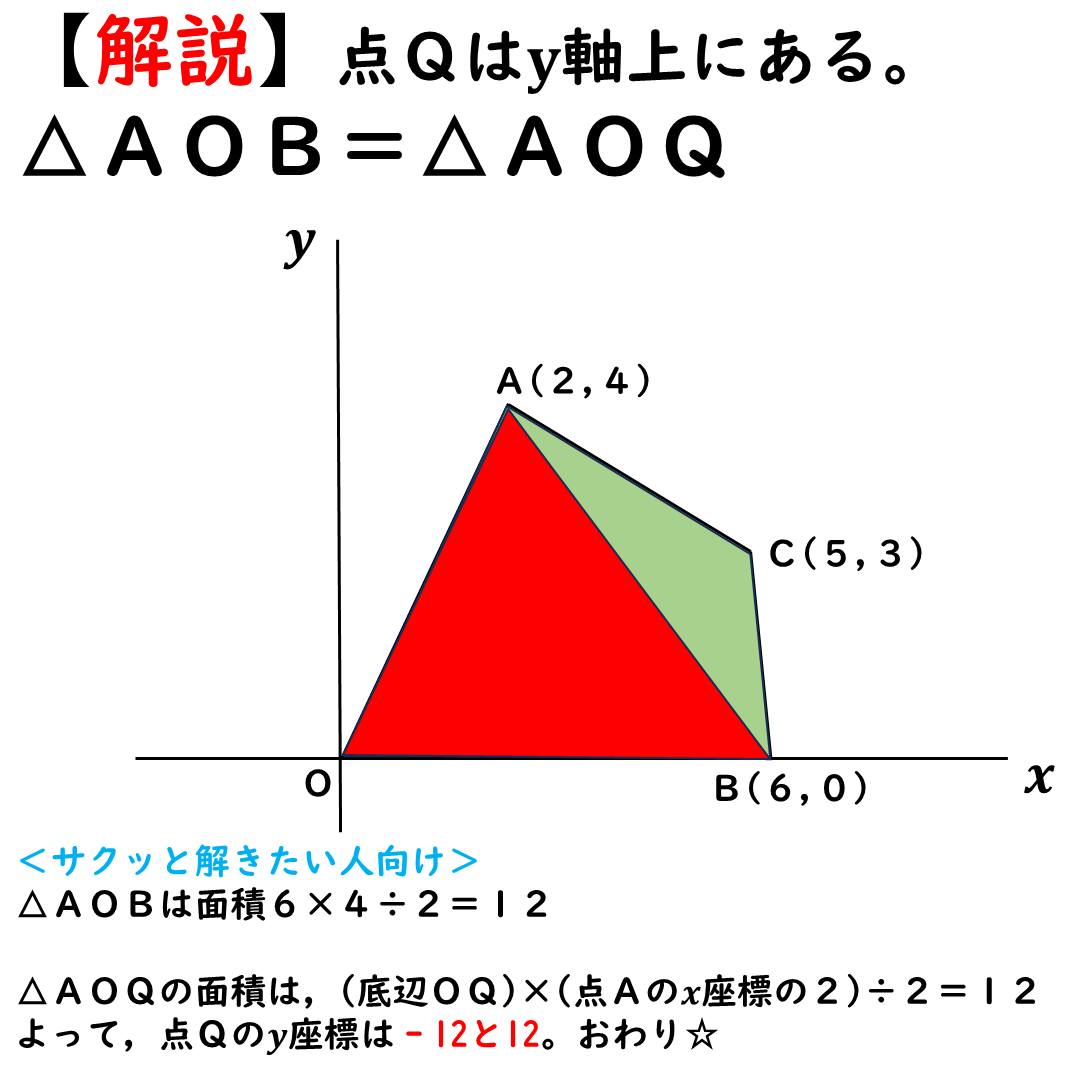
そもそも,
△AOBの面積は12だ。
求めたい△AOQは
(底辺OQ)×(点Aのx座標)÷2
で求まる。
よって,Qのy座標は
-12か12だ。
これでおしまい☆
せっかくだから,
次は等積変形を使って
解いてみようか。
等積変形を使って解く
ここからは,
無理やり等積変形を使って
解く方法を紹介するよ。
グラフや図を
ちょっと縮小したよ!
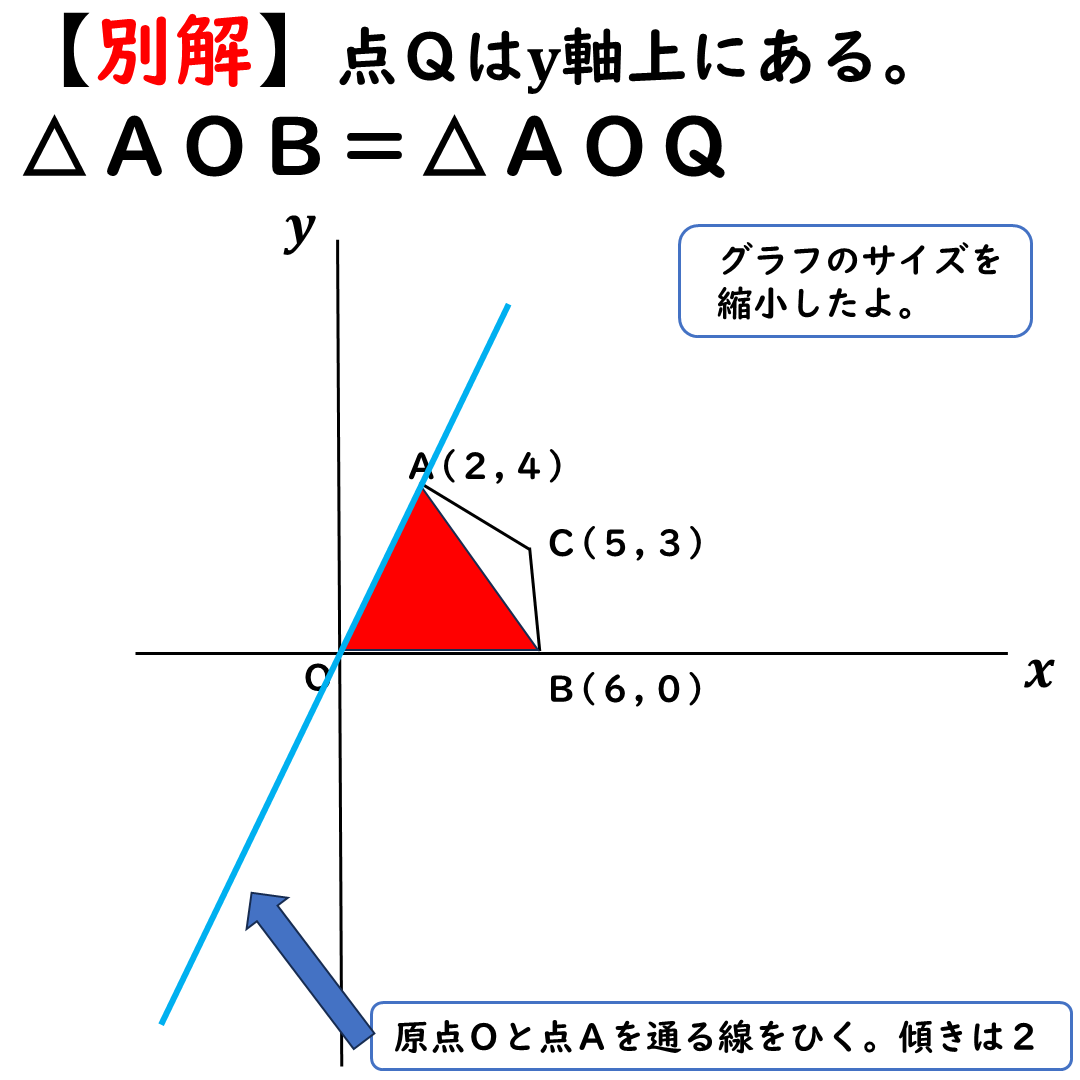
まずは,原点と点Aを通る
補助線をひく。
早速,傾きを求めてしまおう。
A(2,4)を通るから
傾きは2だ。
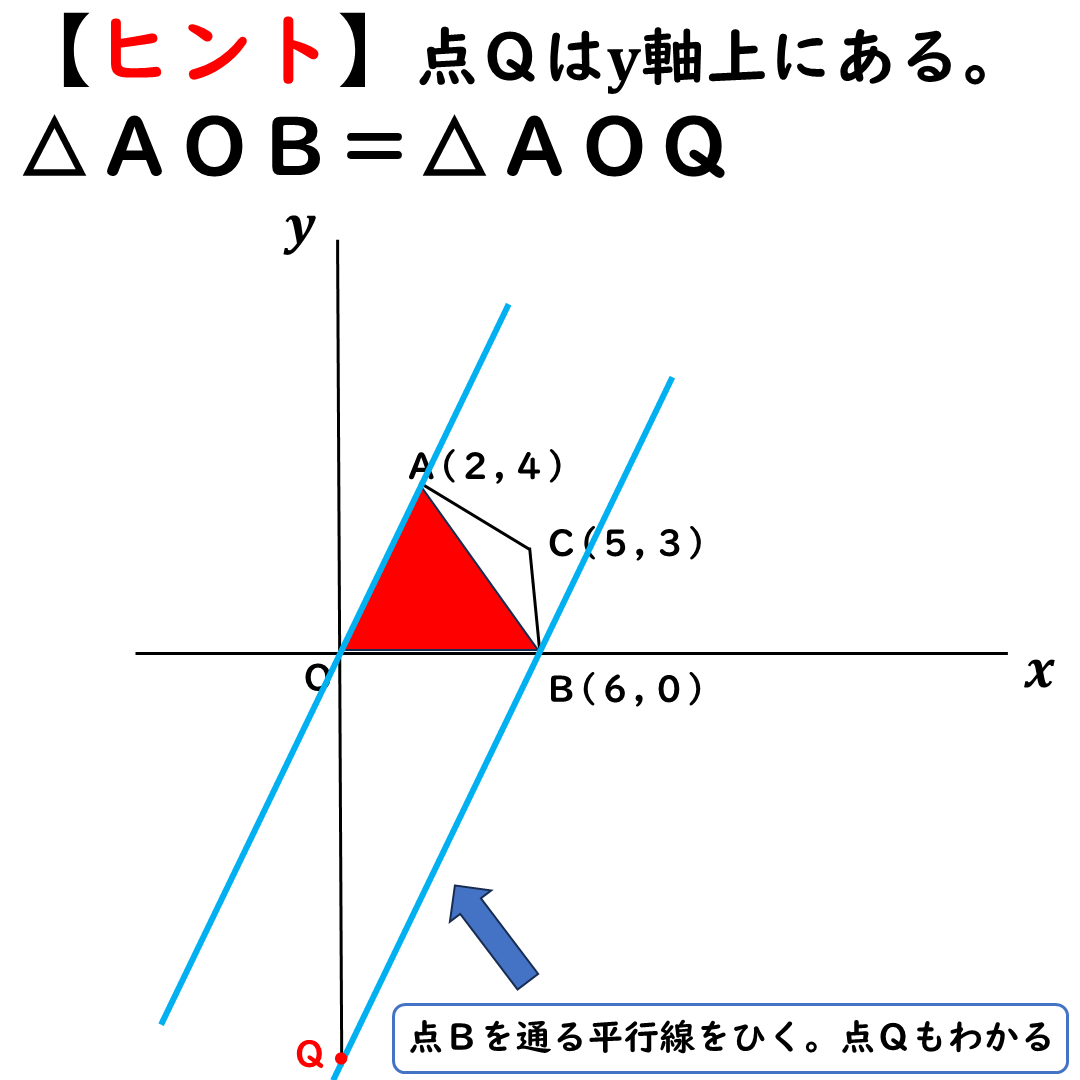
傾き2の平行線を
もう一本ひこう。
点Bを通るようにする。
今から,
△AOBを等積変形していく。
△AOBの等積変形
等積変形のイメージは
こんな感じだ。
何か,
微妙に原点Oが動いてる!
見づらくて申し訳ない。
この等積変形で
△AOB=△AOQになる。
点Qの座標は何だろうか。
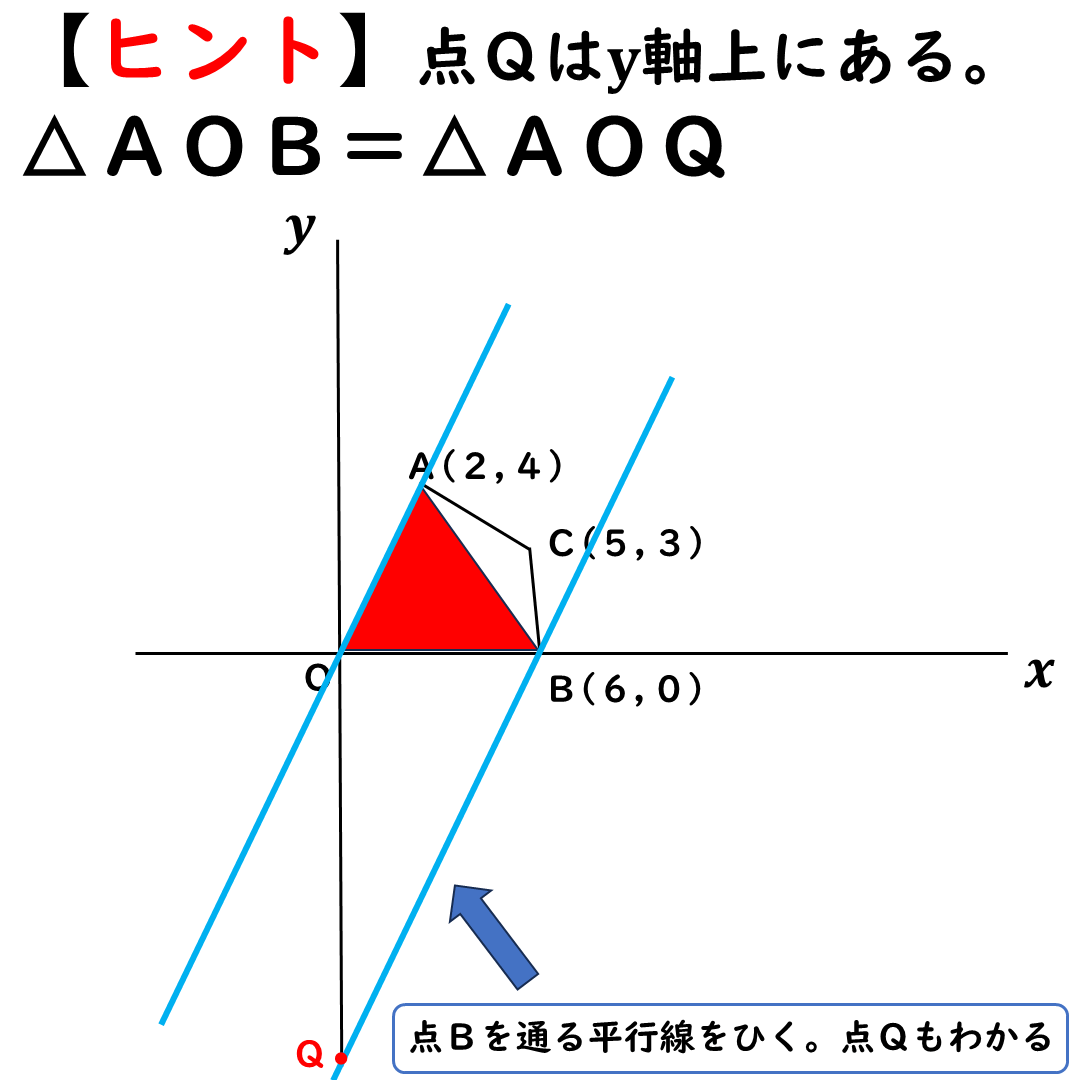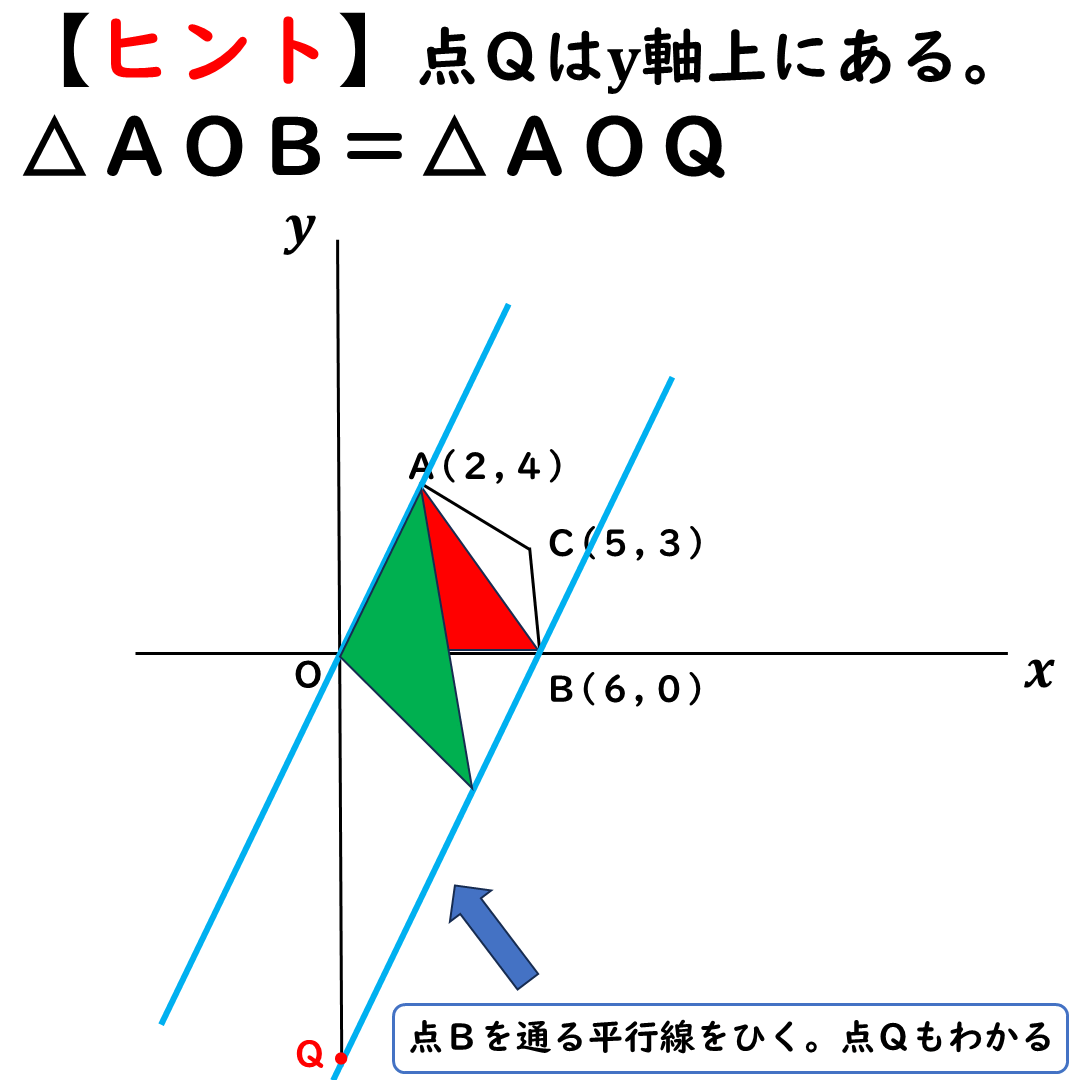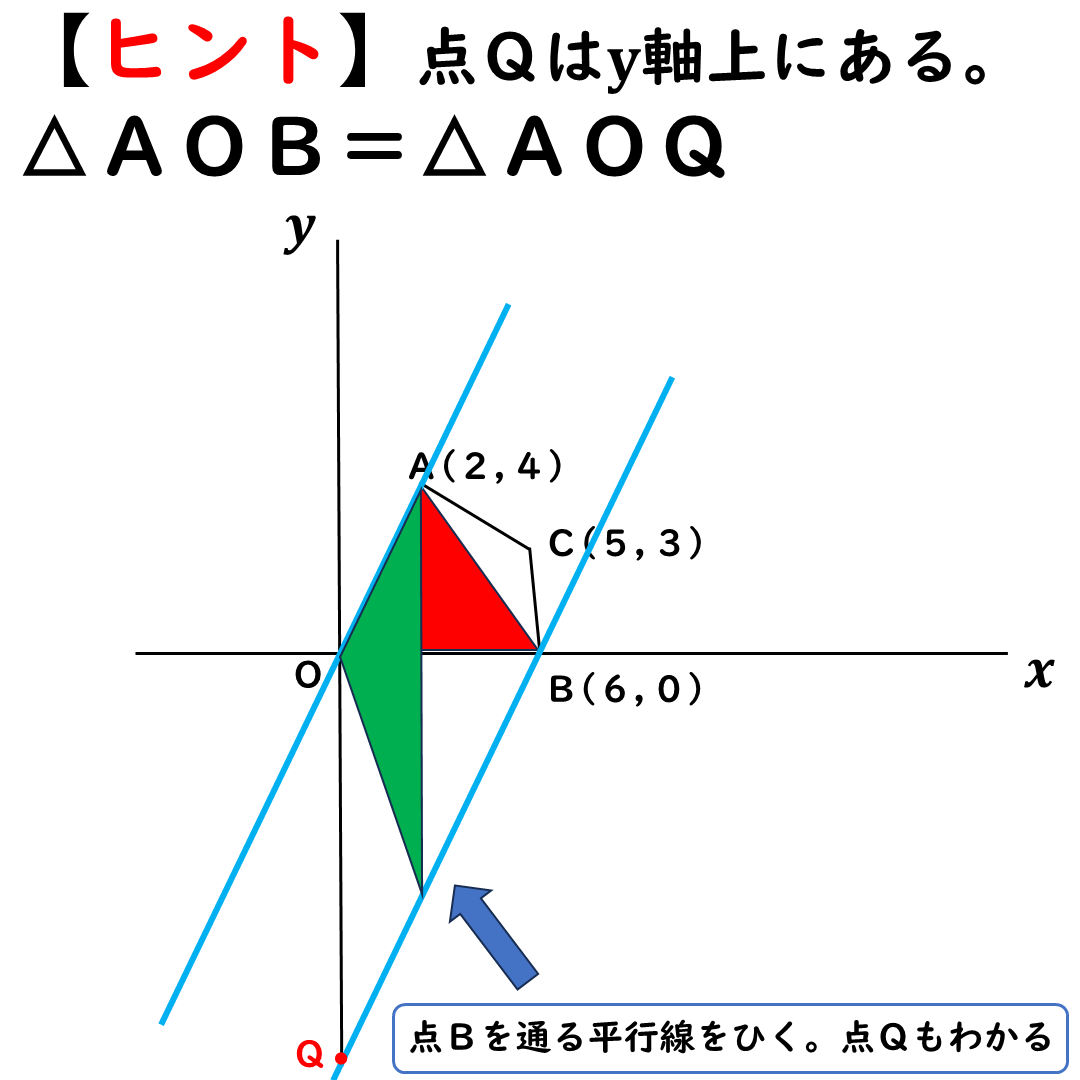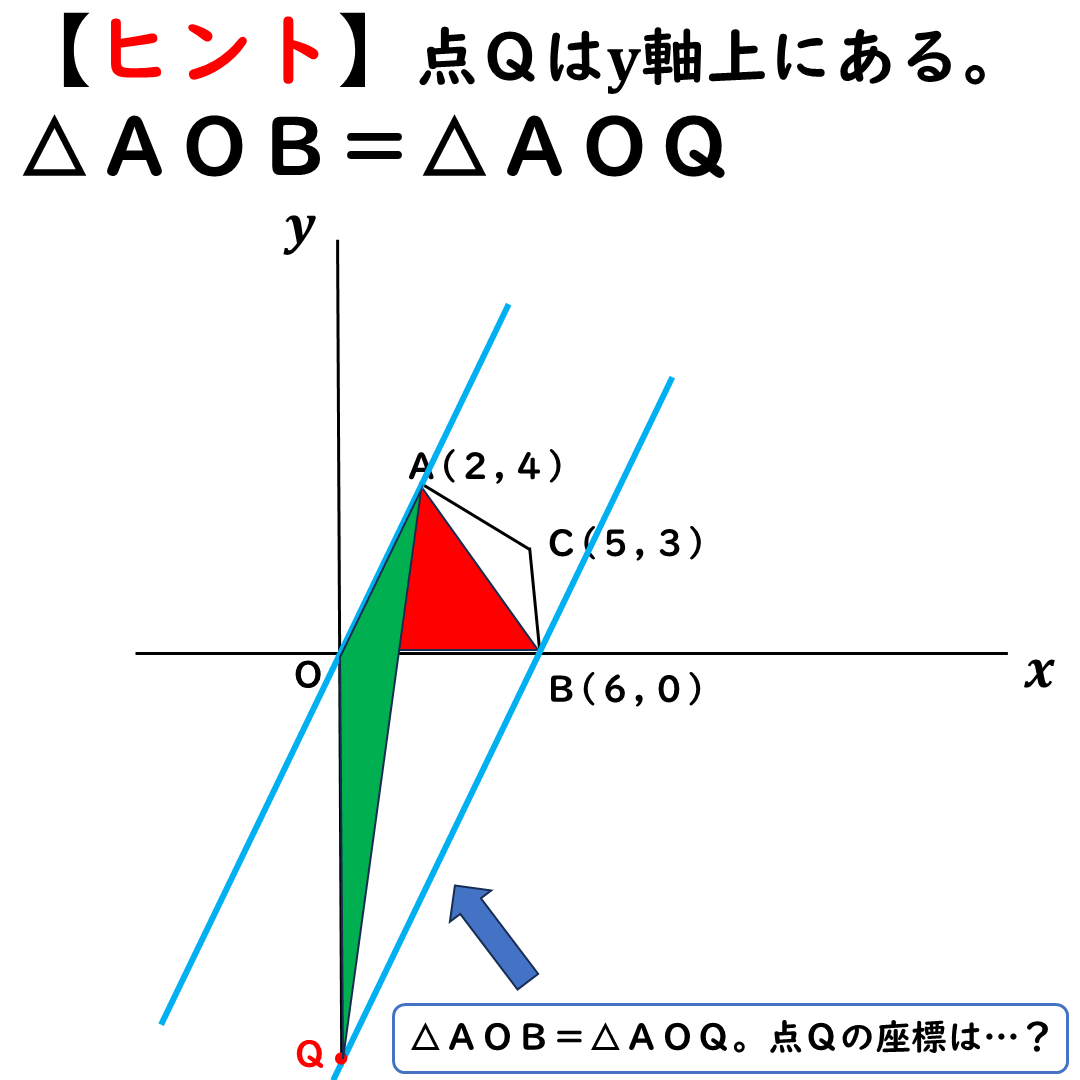
点Qの座標を求める解説
点Qの座標を求めていこう。
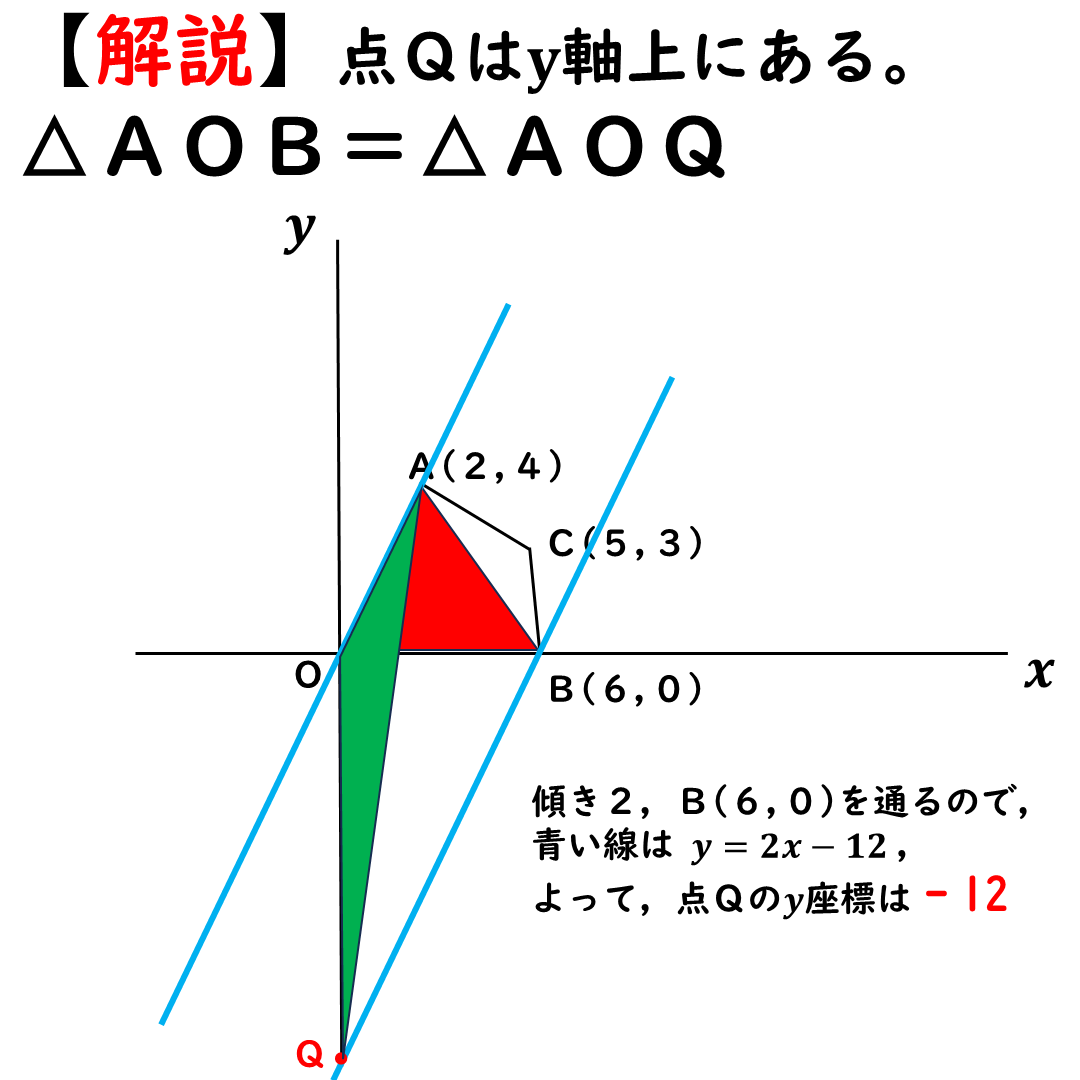
点Qを通る直線は,傾き2で
B(6,0)を通る。
式は,y=2x-12と出てくる。
点Qは切片だよね。
よって,点Qのy座標はー12。
忘れちゃいけないのがもう1個。
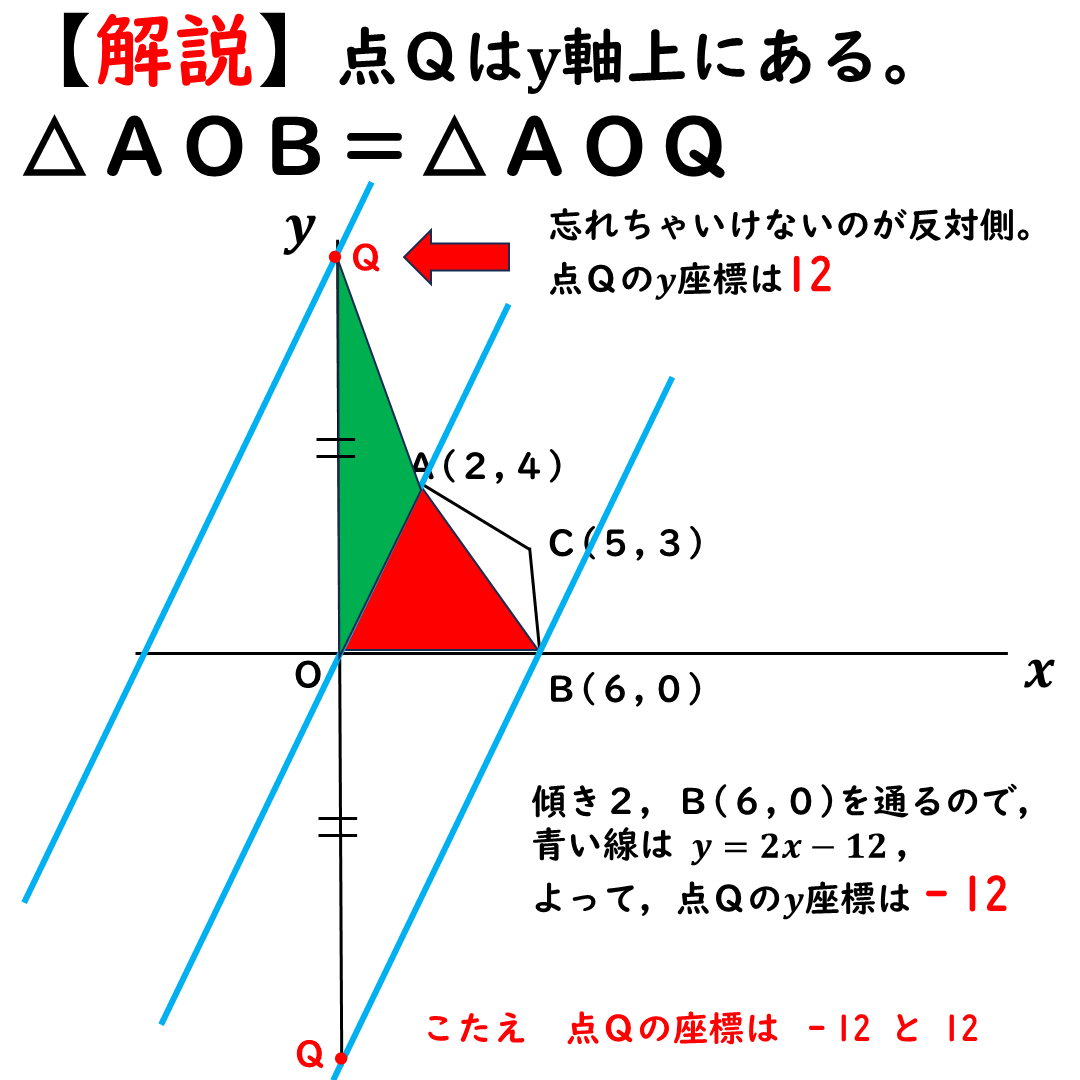
点Qは反対側にもある。
要は,原点から12だけ
離れていればOK。
もう1個の点Qのy座標は12。
答えは,-12,12。
おわりに
今回は,
等積変形について
例題を通して解説しました。
今回のように,
等積変形はグラフと
とても相性が良いです。
中2の後半からの
数学の実力テストに
注文してみてください。
おそらく,等積変形を使った
問題が多いはず☆
この機会にぜひ身に付けてみてね!





コメントはこちらからどうぞ☆