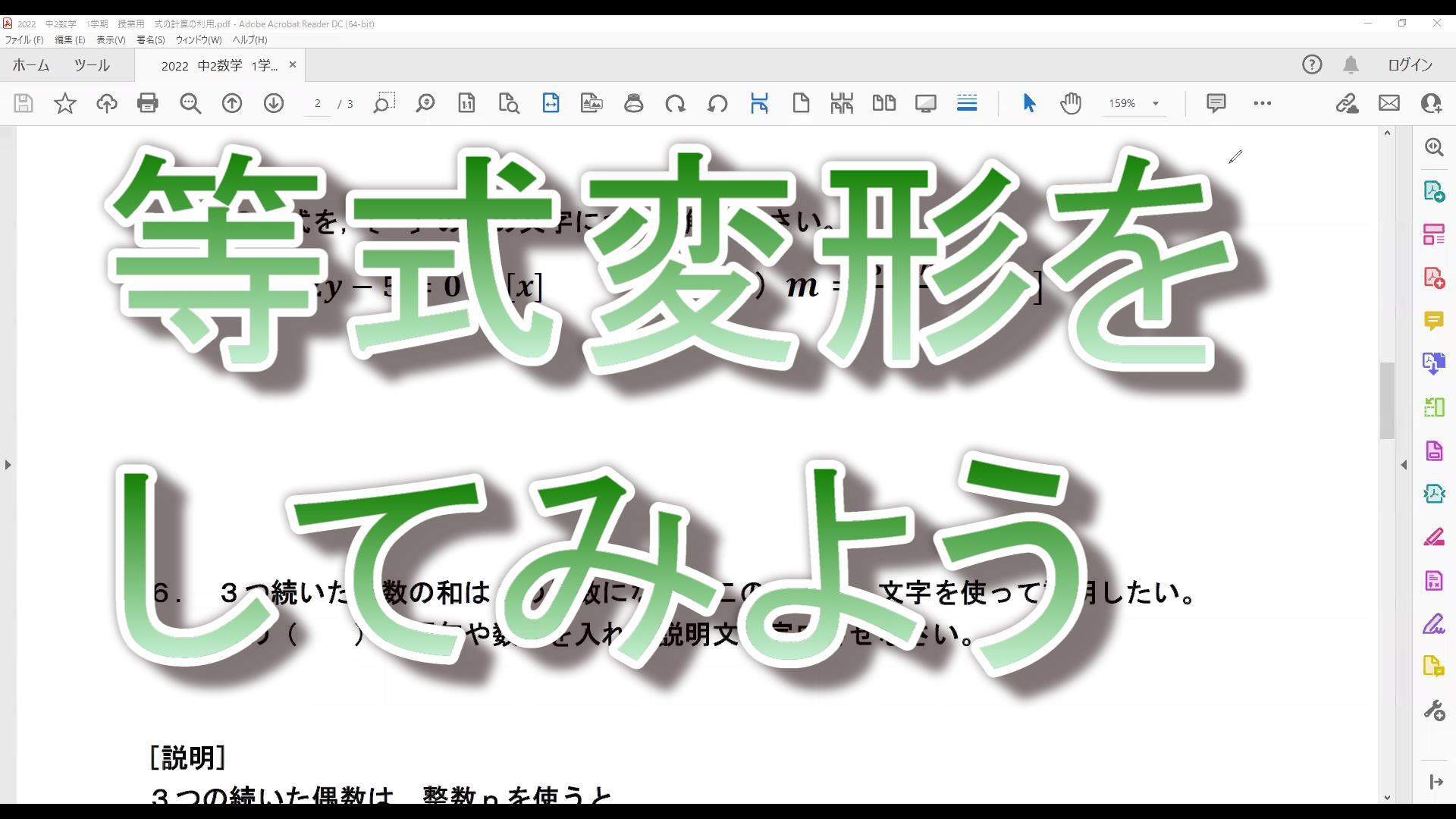
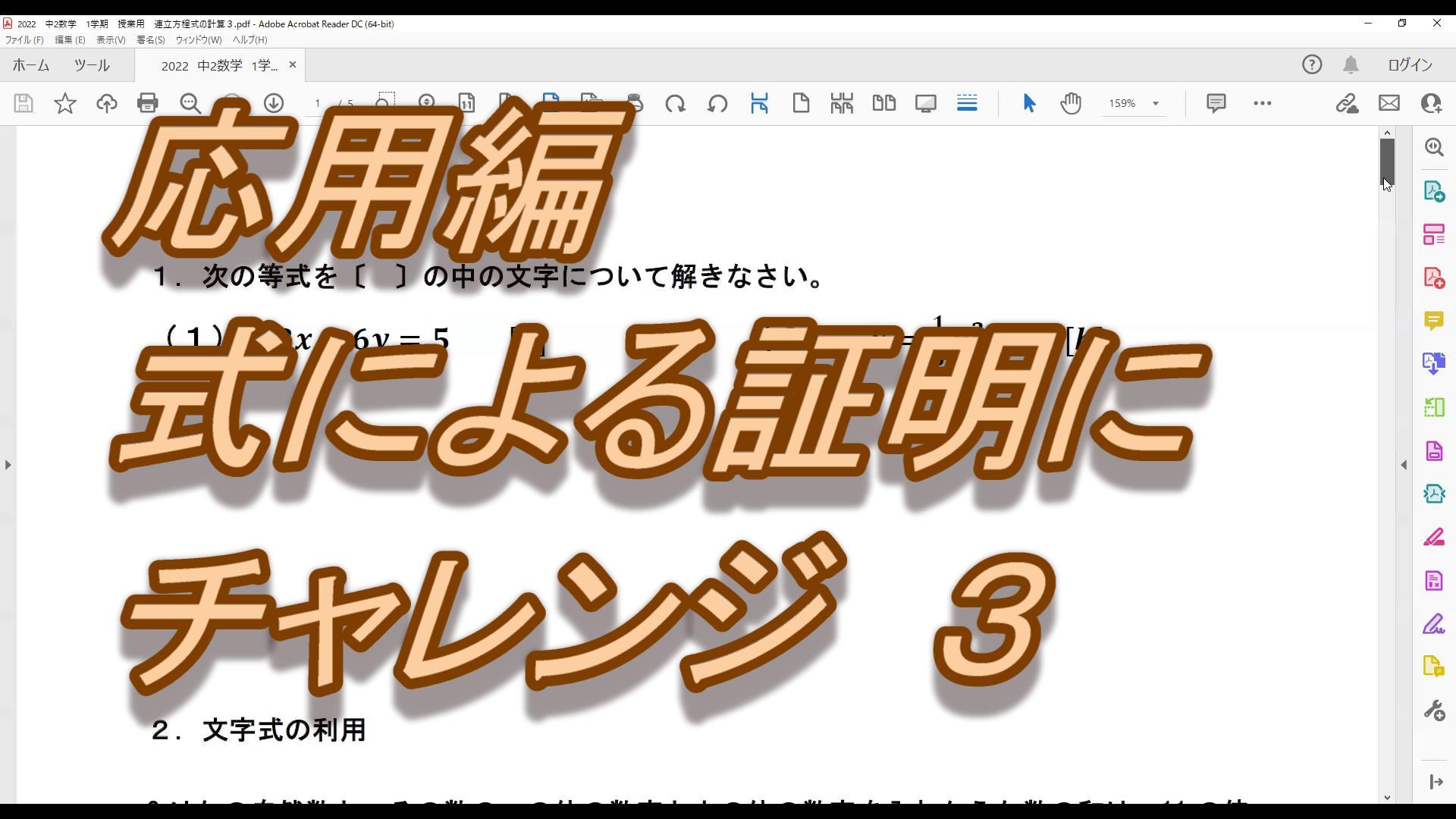
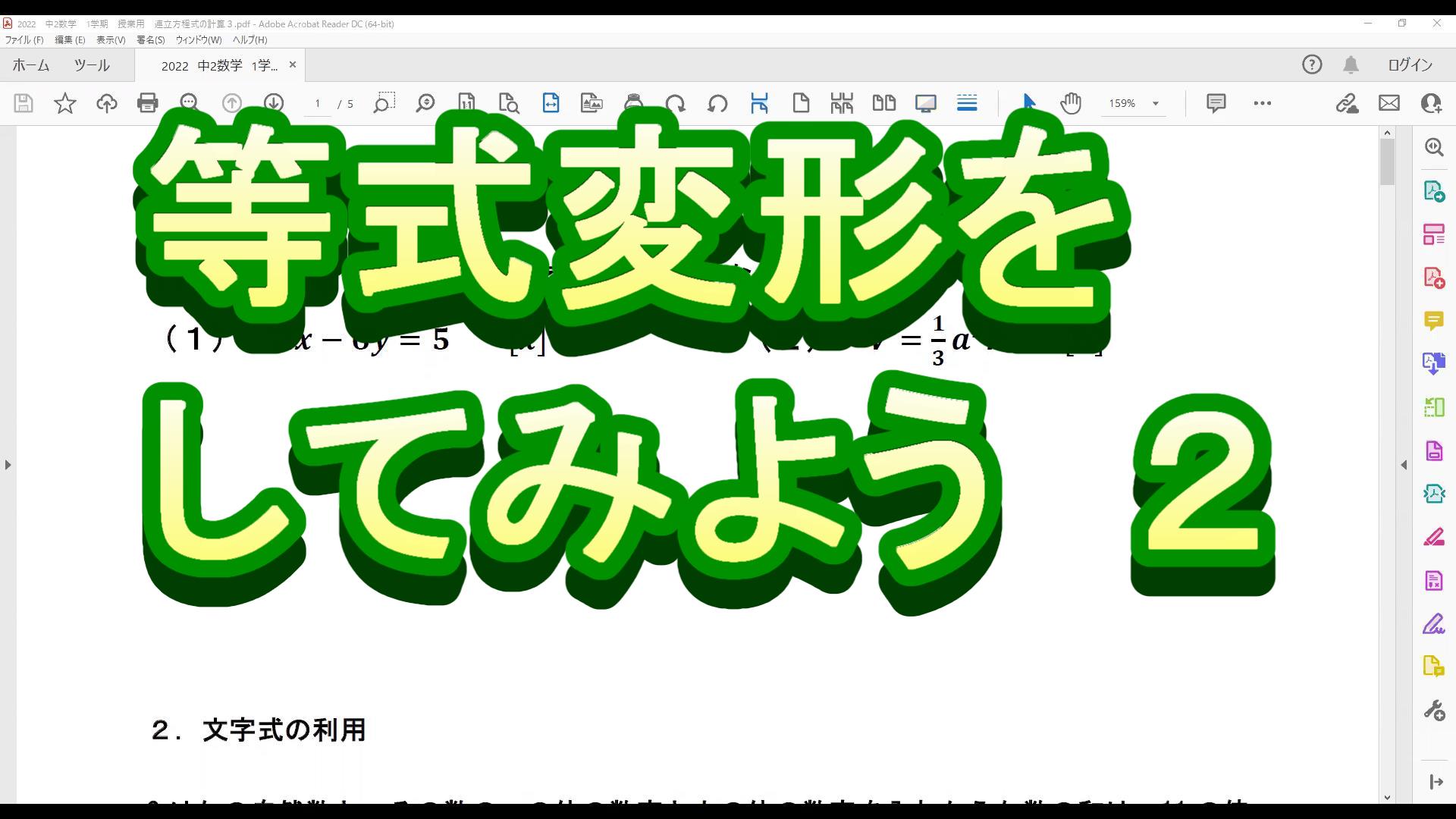
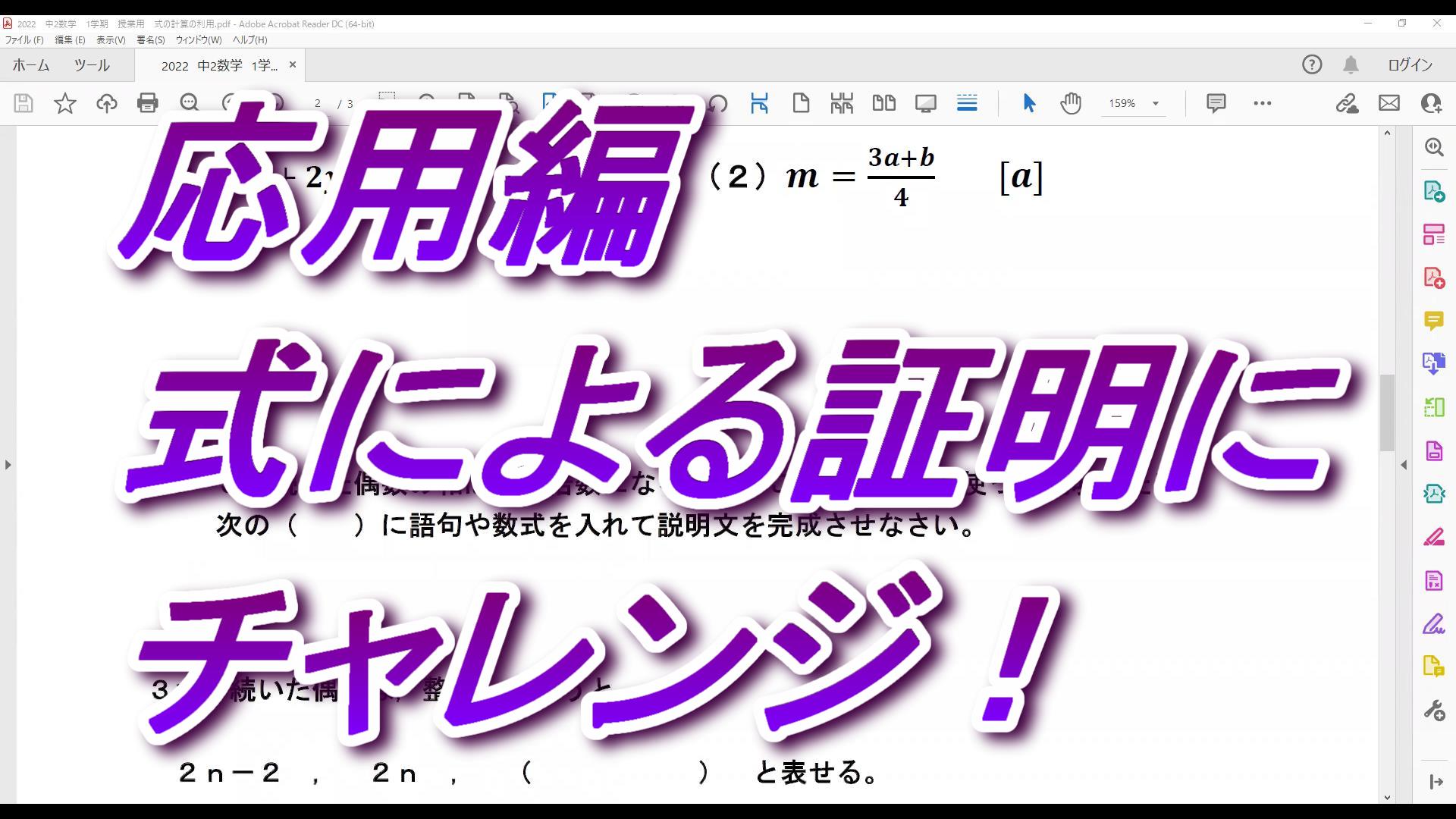
目次
応用編! 式による証明にチャレンジしよう!その2

次の問題にチャレンジしてみよう!
<問題>
2つ続いた奇数の和は
4の倍数になる。
このことを文字を使って
説明しよう。
例えば,
3+5=8
11+13=24
たしかに,4の倍数になりそうです。
これを文字を使って説明する問題です。
<ヒント>
偶数は整数nを使うと2nで表せる。
奇数は偶数の隣にあるから,
2nー1または2n+1だね。
正解はこちら!
<問題>
2つ続いた奇数の和は
4の倍数になる。
このことを文字を使って
説明しよう。
整数nを使うと,
2つ続いた奇数は,
2n-1,2n+1 と表せる。
その和は, (2n-1)+(2n+1)=4n
nは整数だから,
4nは4の倍数である。
したがって,
2つ続いた奇数の和は4の倍数になる。
(終わり)
実際の授業の様子
生徒さんとのオンライン授業の様子です。
けっこう生々しい2分10秒の切り抜き動画。
動画で一緒に学びながら
取り組んでみてください。