【中学受験】計算，おうぎ形の面積のくふう

本記事では，

中学受験を予定している

小5生，小6生向けです。

計算のくふう，

おうぎ形の面積の求め方を

クイズ形式で出題しています。

ぜひ，ご家庭で

親子そろって

チャレンジしてみてください。

それではいってみよー！

【クイズ①】くふうして計算する

それでは，計算1問出します。

くふうして計算できますが，

そのまま順番に計算してもＯＫ。

ただし，中学受験では，

時間のムダは

不合格につながります。

答えは下にまとめてあります。

まずは自分自身で答えを出そう。

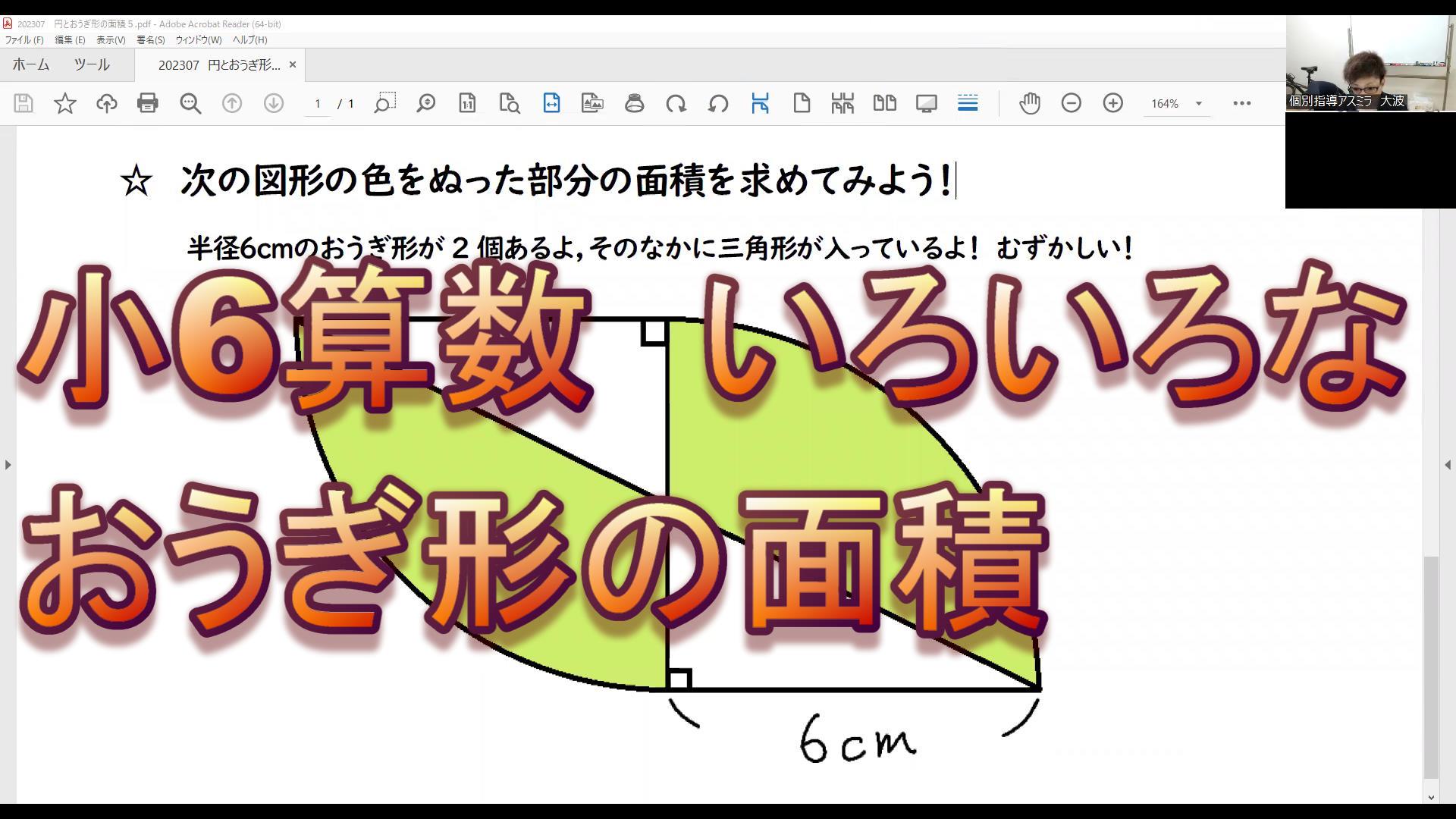
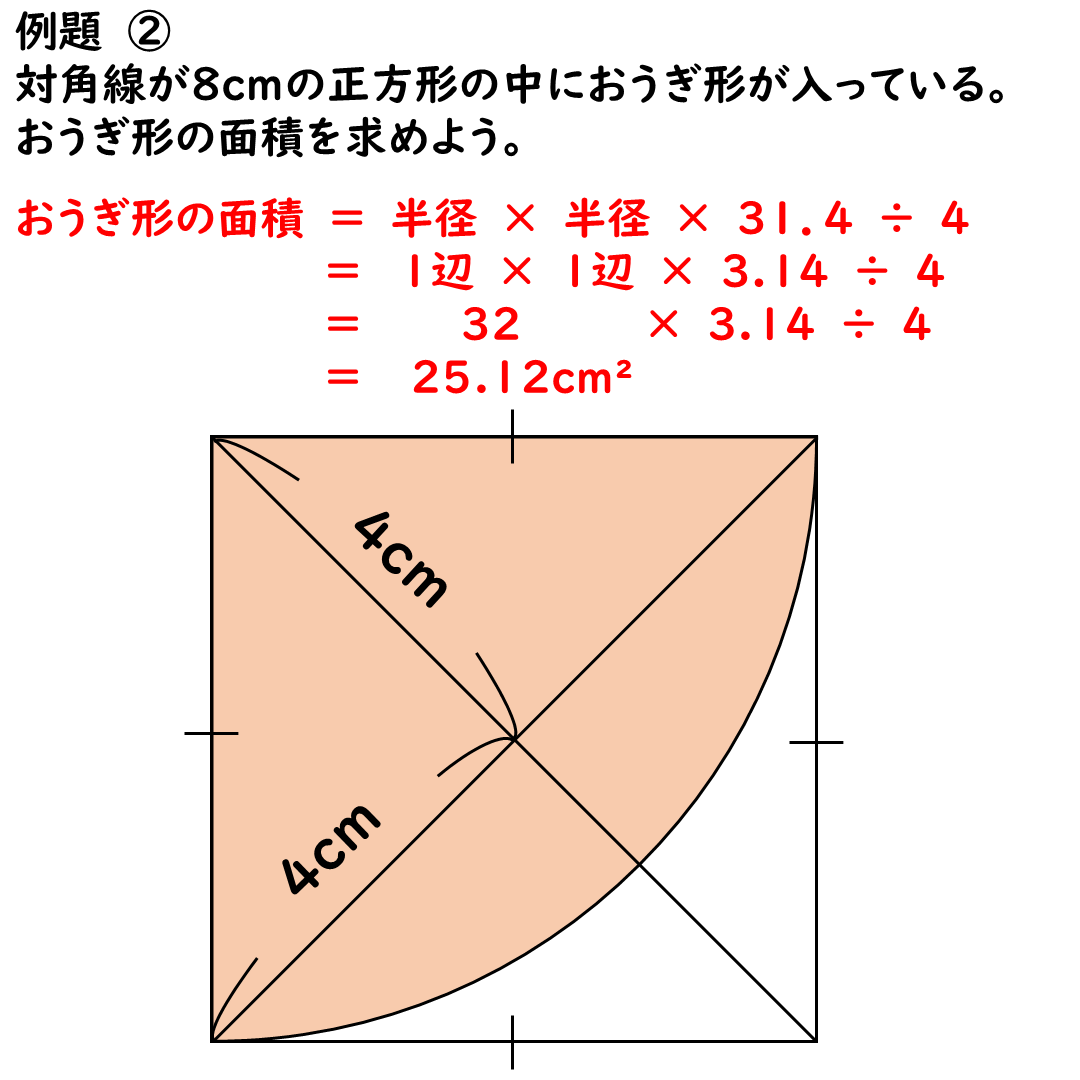
【クイズ②】おうぎ形の面積は？

次は，おうぎ形の面積を求める問題。

正方形のなかにおうぎ形があるから，

求めてみてね。

正方形の対角線が８ｃｍ，

これだけわかっているよ。

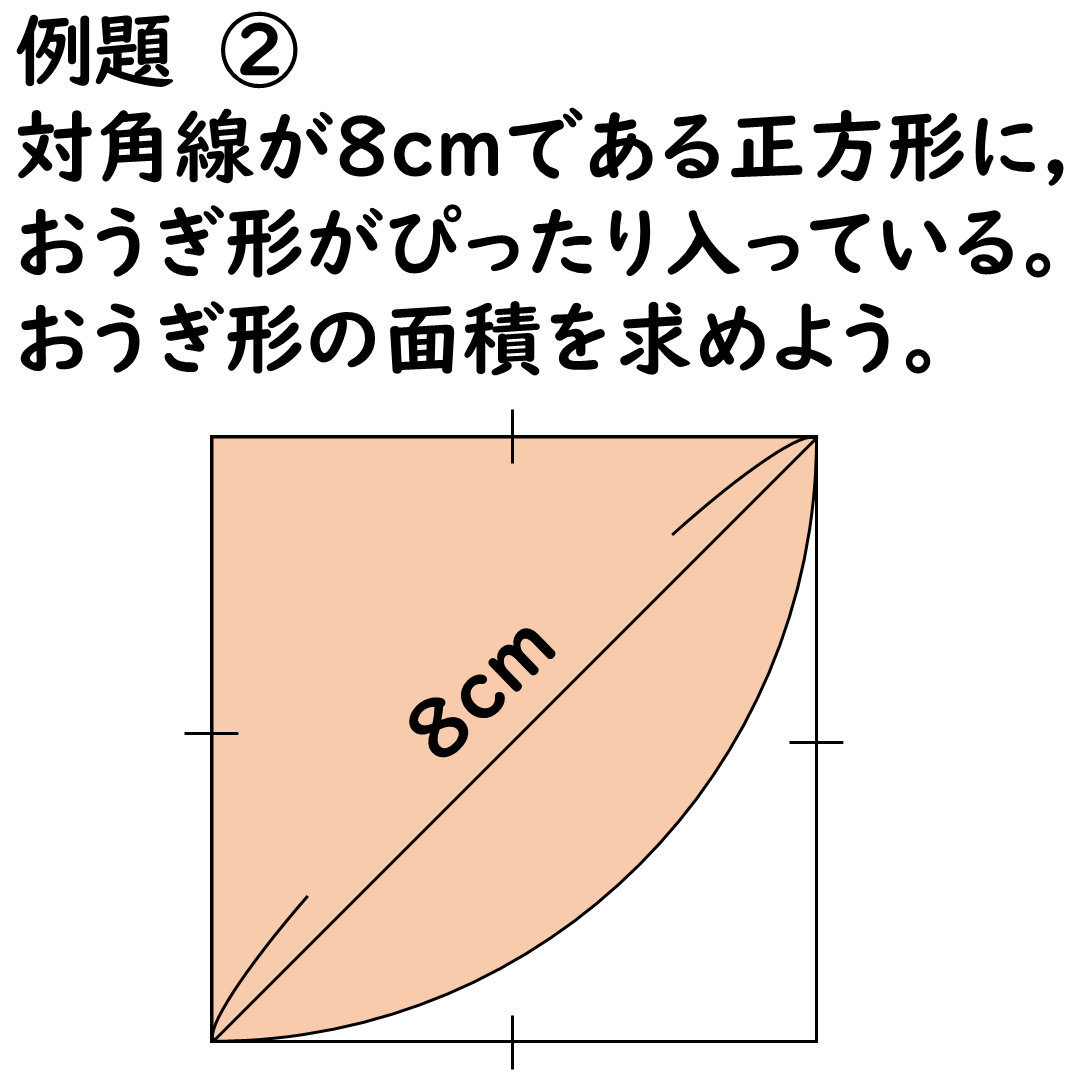
＜ヒント＞

半径を求めるんじゃない。

そんなもんいらねぇ・・・。

半径×半径を求めるんだ。

何でもきちんと求めればいいって

もんじゃない。

途中でいいんだよ。

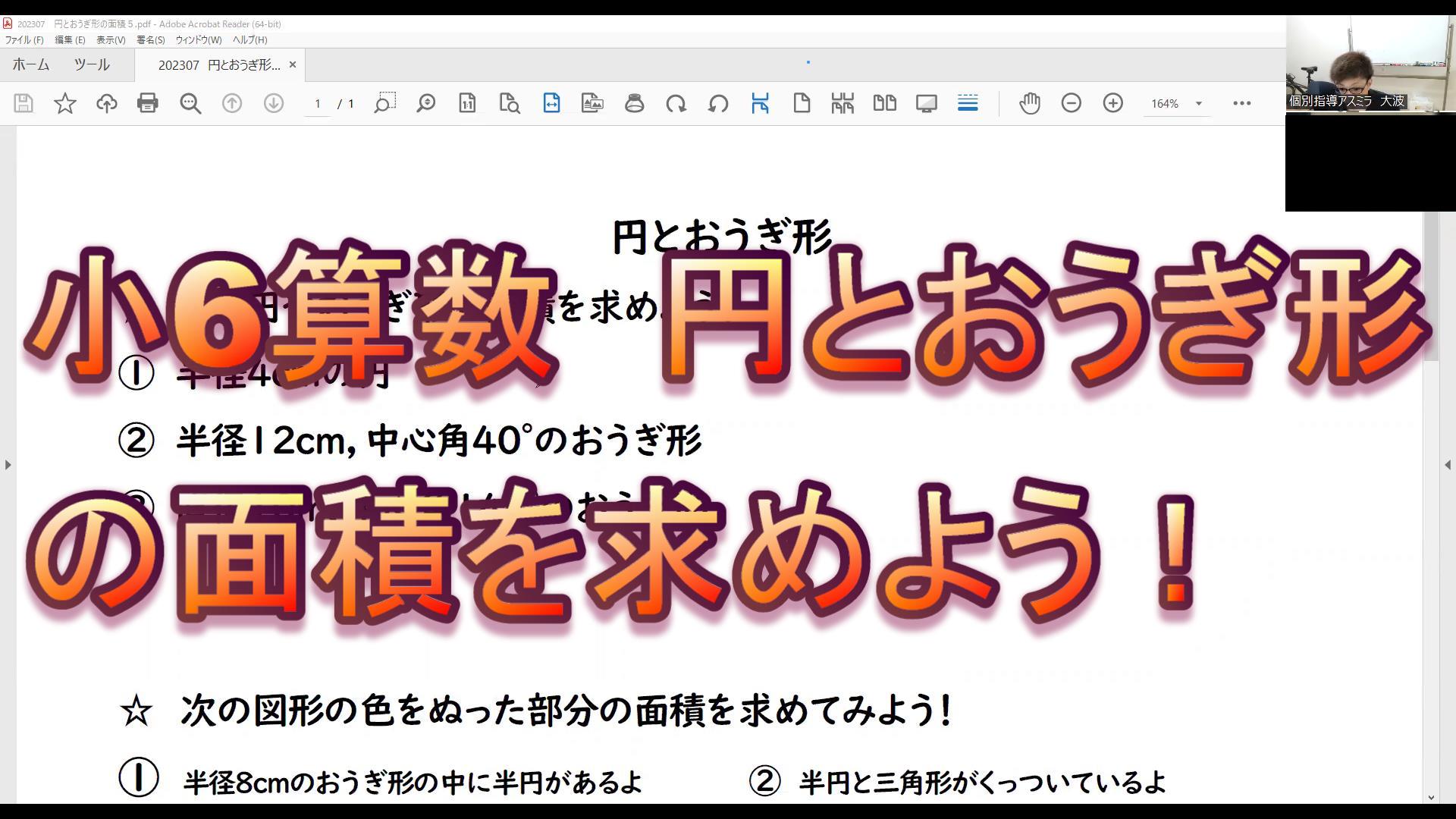
【クイズ③】おうぎ形の面積は？

次もおうぎ形の面積の問題だ。

気付けば1分以内。

気付けないと苦労する。

そういうネタの問題。

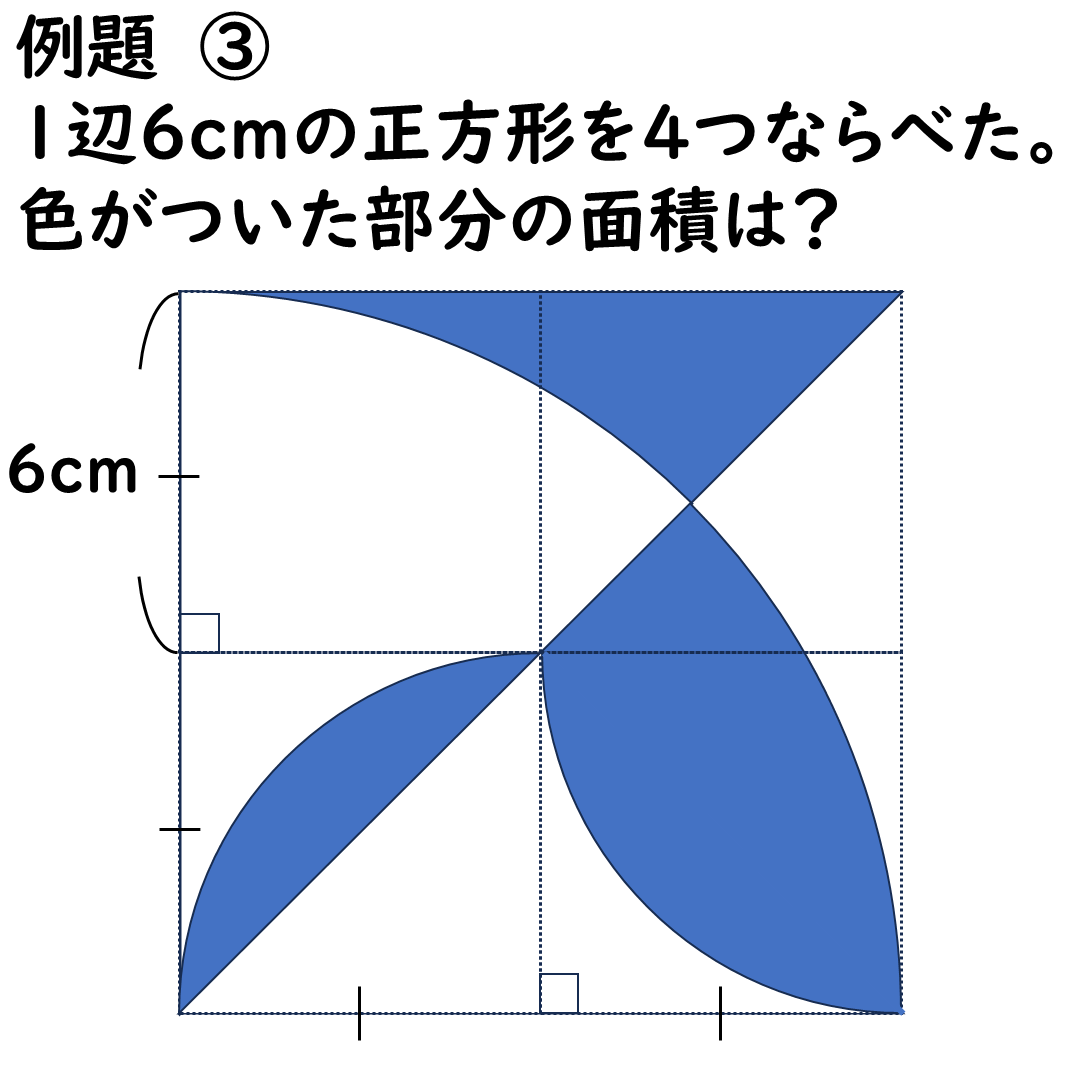
＜ヒント＞

ただのパズルゲームだ。

動かしてみよう。

１つ１つ求めたら負け。

こたえと解説

こたえを載せます。

丸付けしてみてね。

①　62.8

②　25.12ｃｍ^２

③　56.52ｃｍ^２

クイズ①の解説

①は，314でまとめて解いてみます。

もちろん，3.14でまとめてもいいし

31.4でも解けますよ。

次に，314を残して他を計算します。

最後に314でまとめます。

保護者の方へのおねがい

私がそばにいたら，

次のような視点を持つので

お子さんとチェックしてみてください。

今回は314でまとめましたが，

3.14でまとめたらどんな計算過程に

なるだろうか。

31.4でもできるだろうか。

実際にやってみるのが大切です。

大抵の人はまずやりませんからね。

体験的な学習でない限り

身に付きません。

そもそも身に付いているなら

こんなページなんて見てないはずです。

実際に，再度解いてみてください。

次に，

解説でようやく理解した場合について。

テスト中に気付くためには，

今後どこに注目すると良さそうか

お子さんと具体的に作戦を立てます。

これはお子さんごとに異なります。

わからなければご相談ください。

他にも，そのまま順に計算しても

解けるけど，

どちらが速いか正確か。

解ければタイムロスしてもいいのか。

その際に何が問題になるか。

これも話し合ってみてください。

次に，

お子さんの計算過程の書き方。

どこに過程を書いているか，

どのように書いているか。

見返して読める再現性はあるか。

そもそも暗算で何も書いてないか。

＼これが一番怖いパターンかも☆／

クイズ②の解説

この問題，

正方形の1辺，つまり

おうぎ形の半径が

求められないんですよね。

半径がわからないから

無理！

そうやって捨ててしまうお子さん

多いのかなと予想しています。

たぶん，そのお子さんは，

しっかり，きっちり，

順番にていねいに求めてきた

優秀なお子さんだと思います。

だから，あえてココで

学んでほしい。

中途半端でいいんだよと。

そういう戦い方もあると。

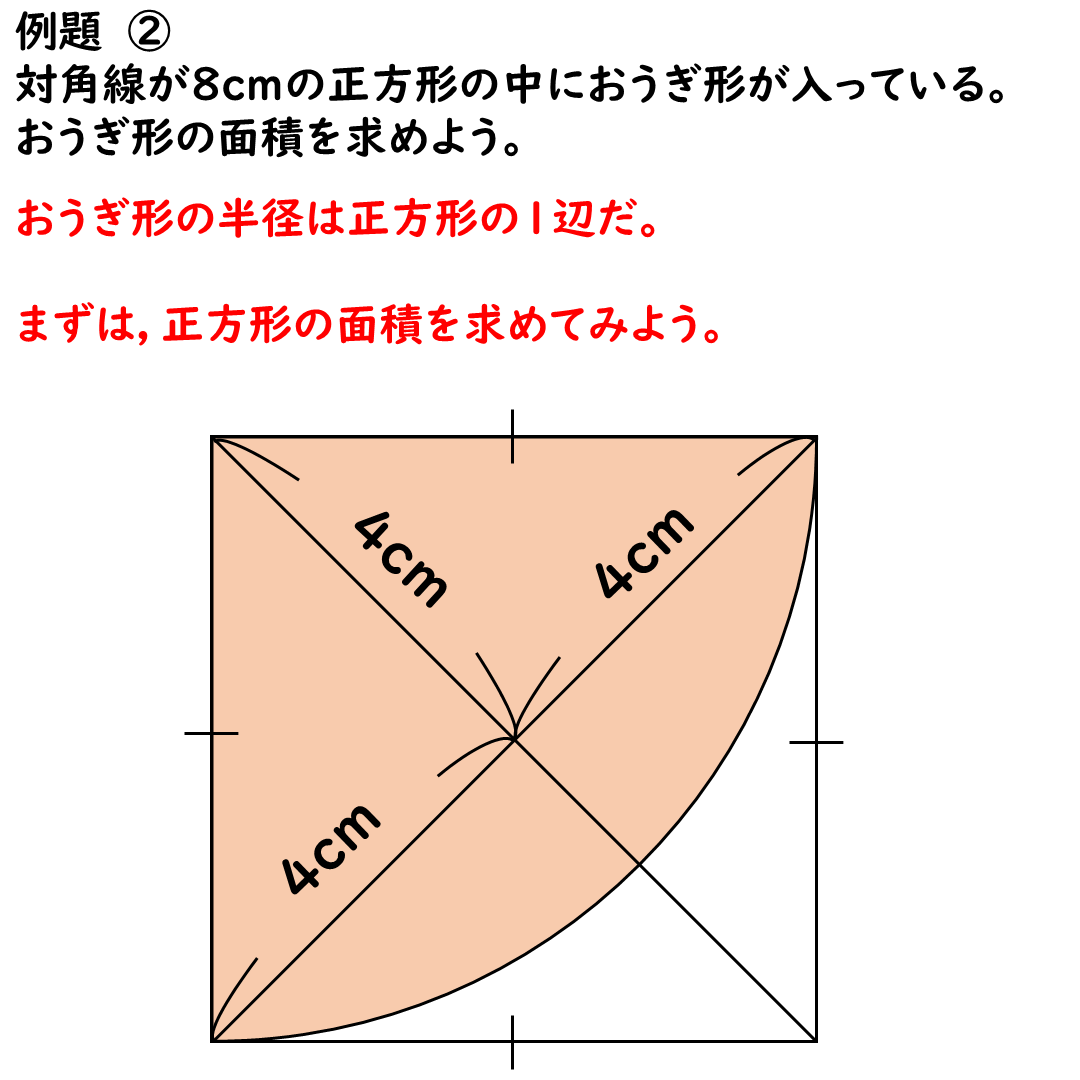
まずは，

正方形の面積を求めてみます。

対角線×対角線÷２でいいけれど

あえて三角形でやってみます。

正方形の面積は３２ｃｍ^２

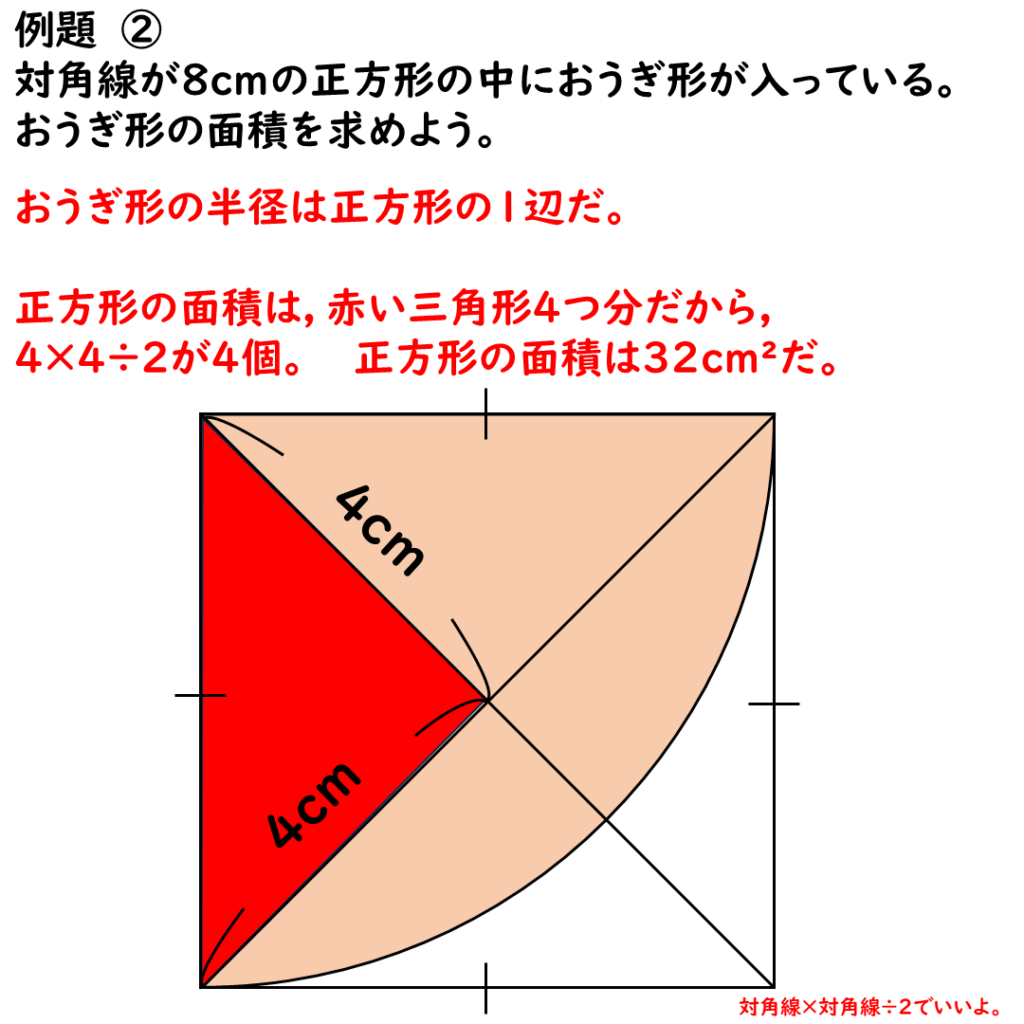
これが何になるのか・・・。

実はこれでいいのである。

正方形の面積＝1辺×1辺 だ。

つまり，

３２＝　1辺×1辺

今回の図でいくと，

正方形の1辺はおうぎ形の半径

と同じ位置だ。

1辺×1辺＝半径×半径＝３２

これをそのまま使います。

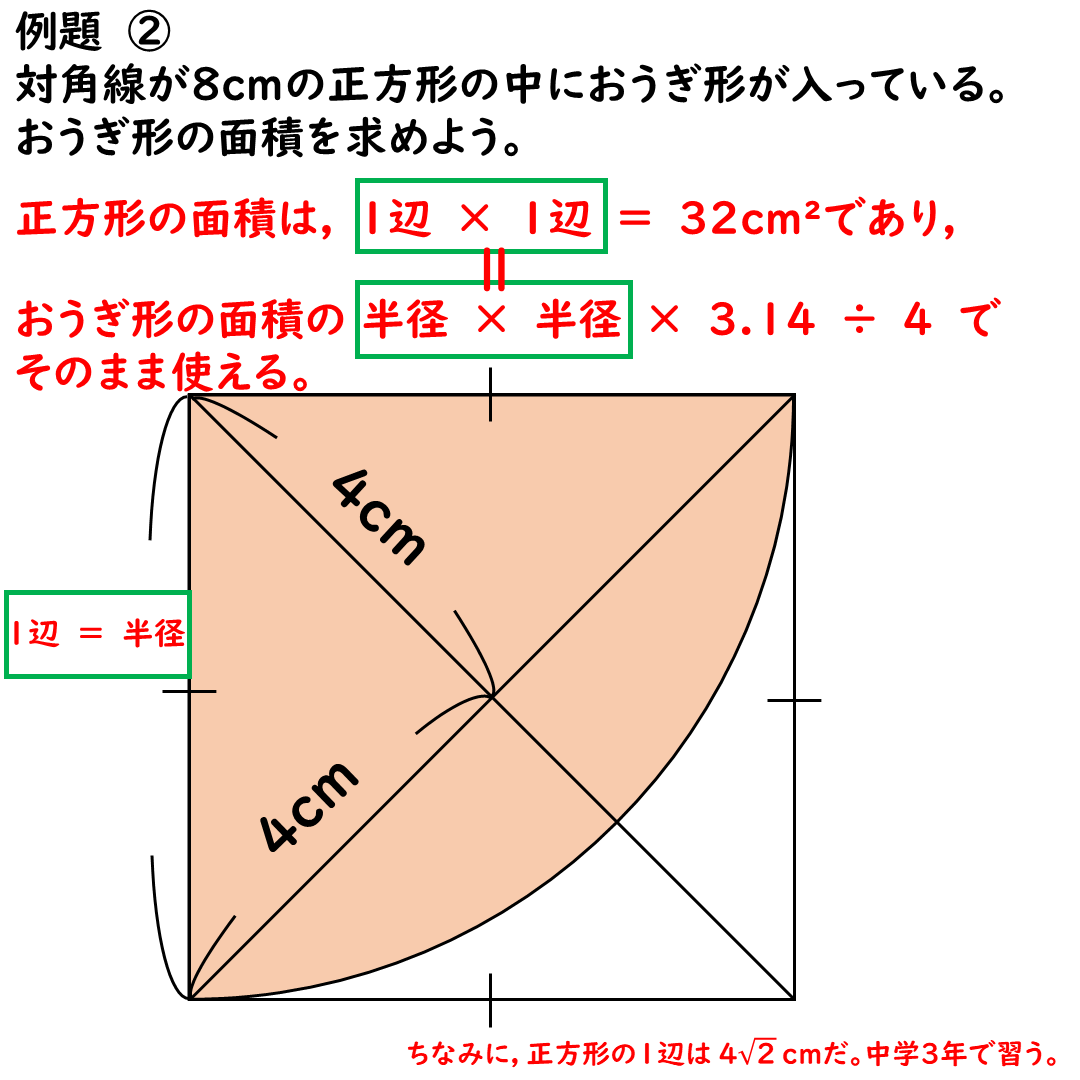
あとは，

おうぎ形の面積の求め方にあてはめて，

半径×半径×3.14÷4をします。

ちなみに，半径自体の大きさは

中学3年にならないと

表せません。

もし，お子さんに

半径の求め方を聞かれたら

3年後，中3になったあなたが

必ず解決してくれるよ☆

などと返すと良いでしょう。

クイズ③の解説

これはヒントにも書きましたが

ホントにただのパズルゲーム。

図形移動するだけです。

実際にやってみます。

まずは赤い部分の面積を

ひっくり返して移動します。

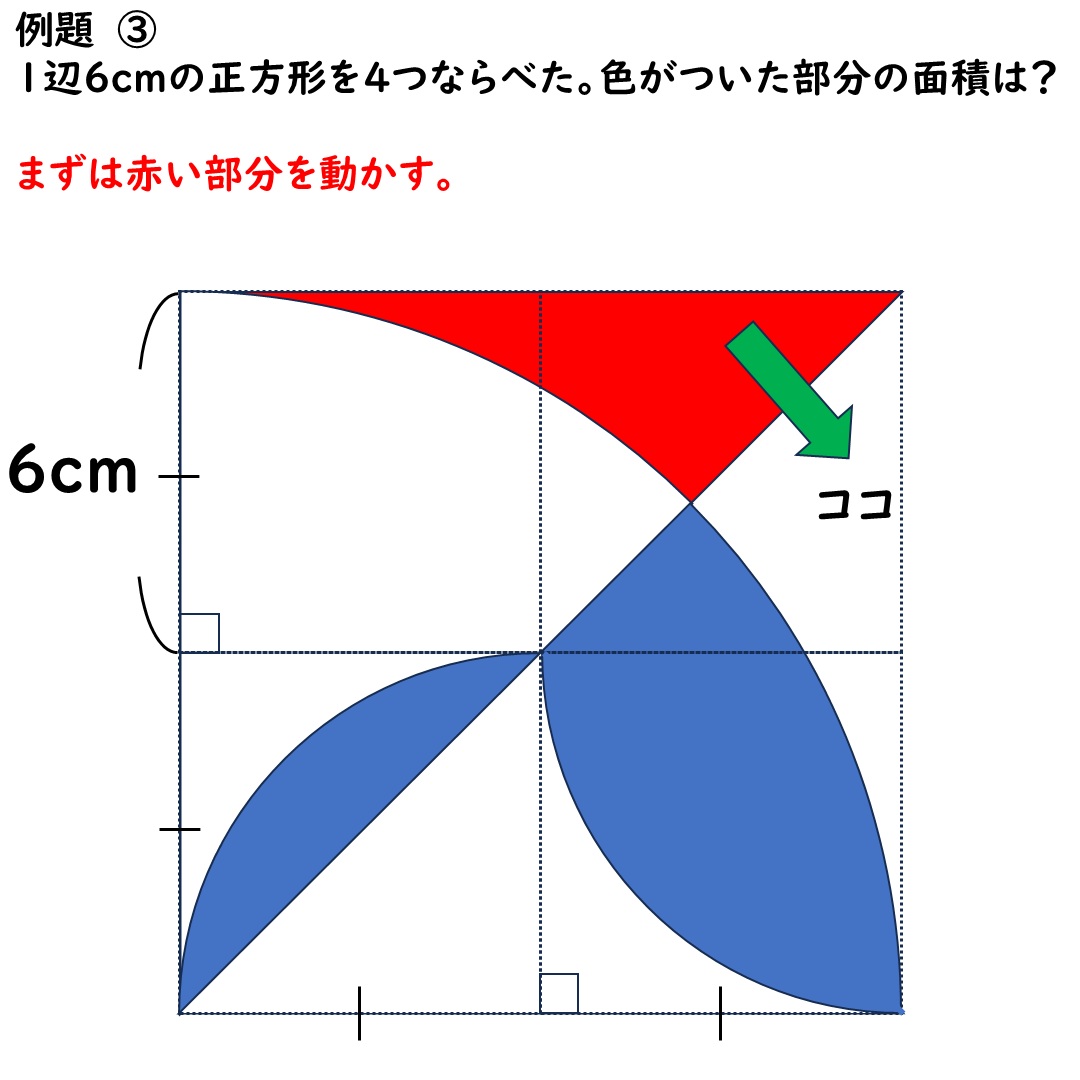
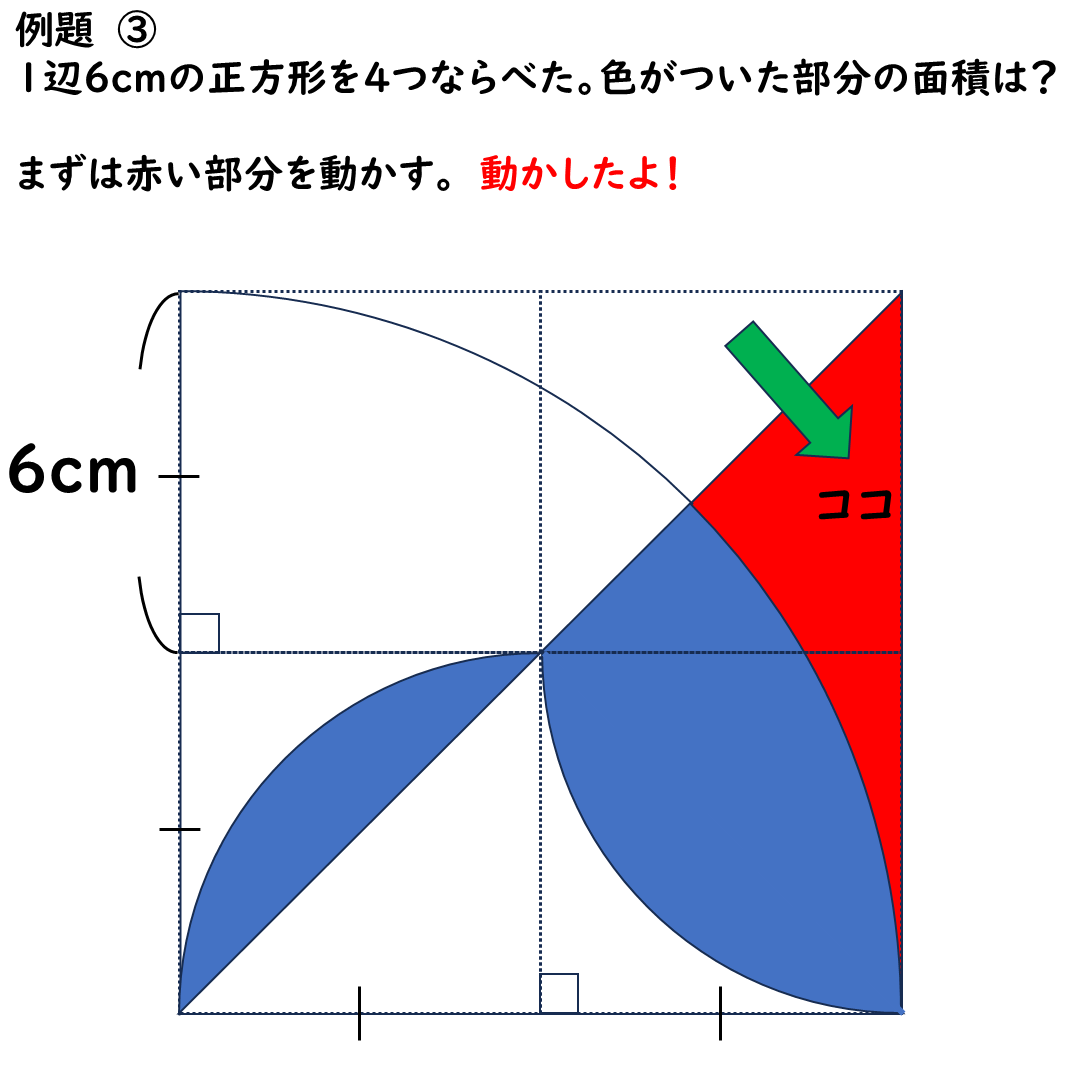
こんな感じになります。

なんとなく，

ネタがバレてきた予感☆。

もう１つ移動します。

次は紫色の部分を移動する。

ななめ上に動かします。

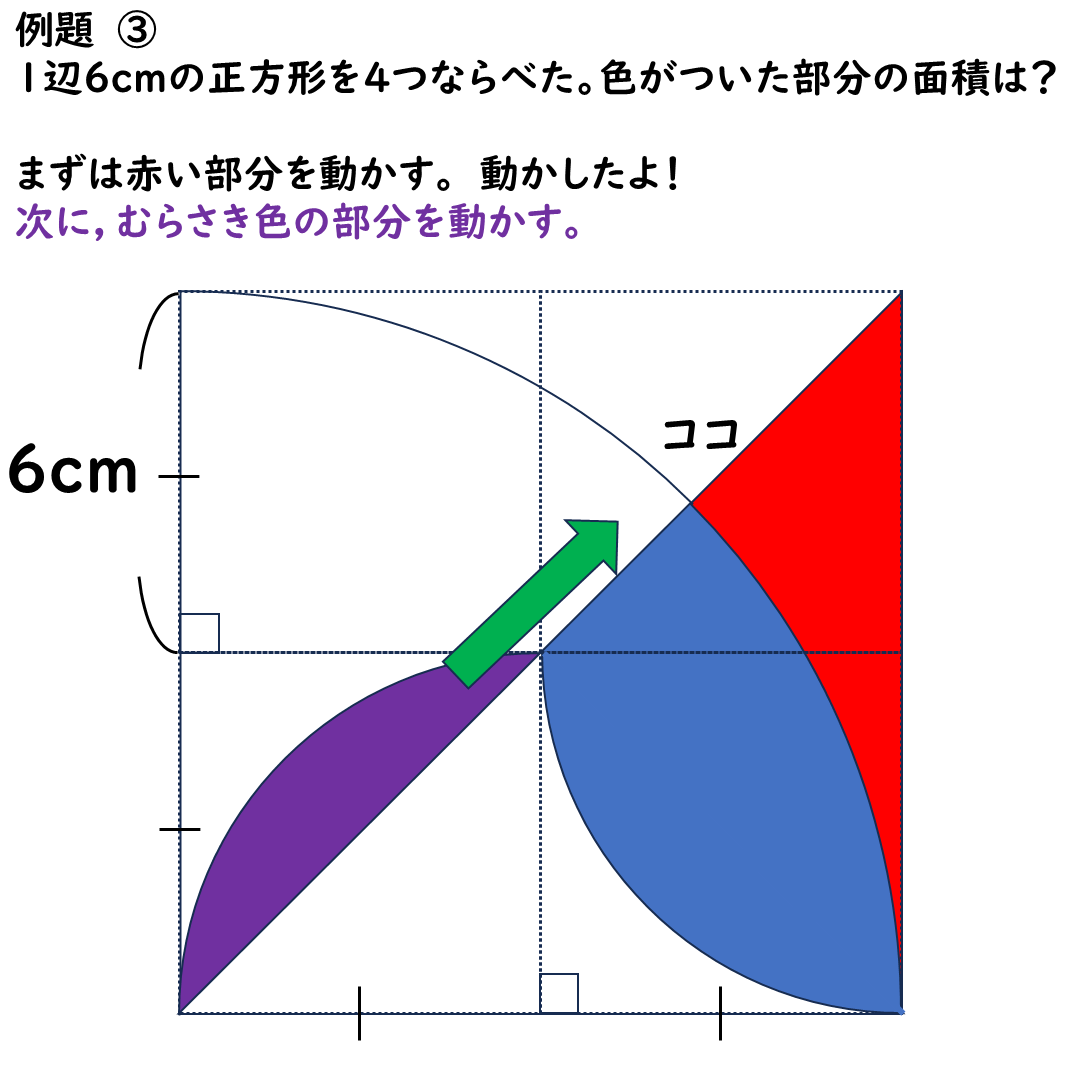
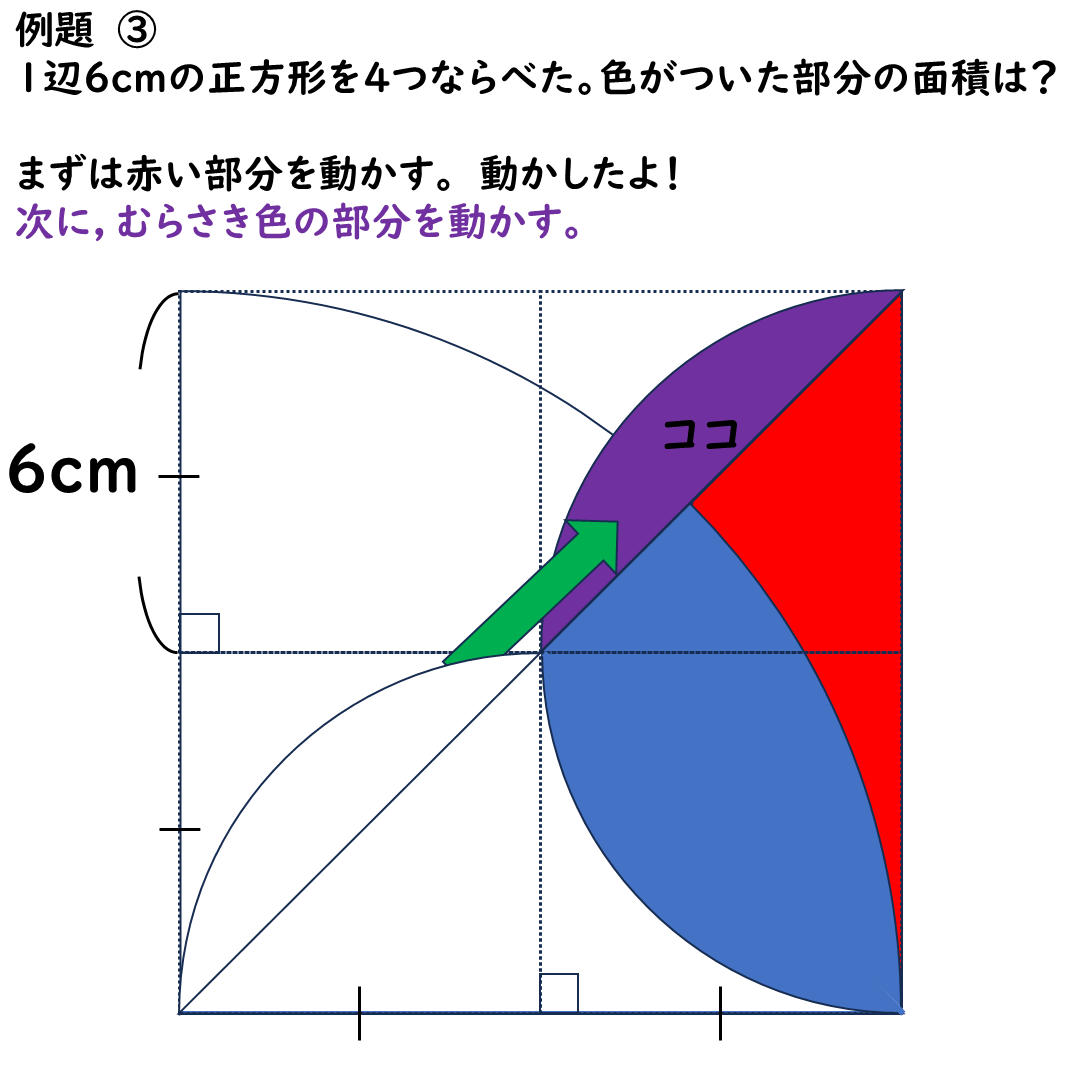
そうすると，

こんな感じになります。

これで完成。

半径６ｃｍの半円になります。

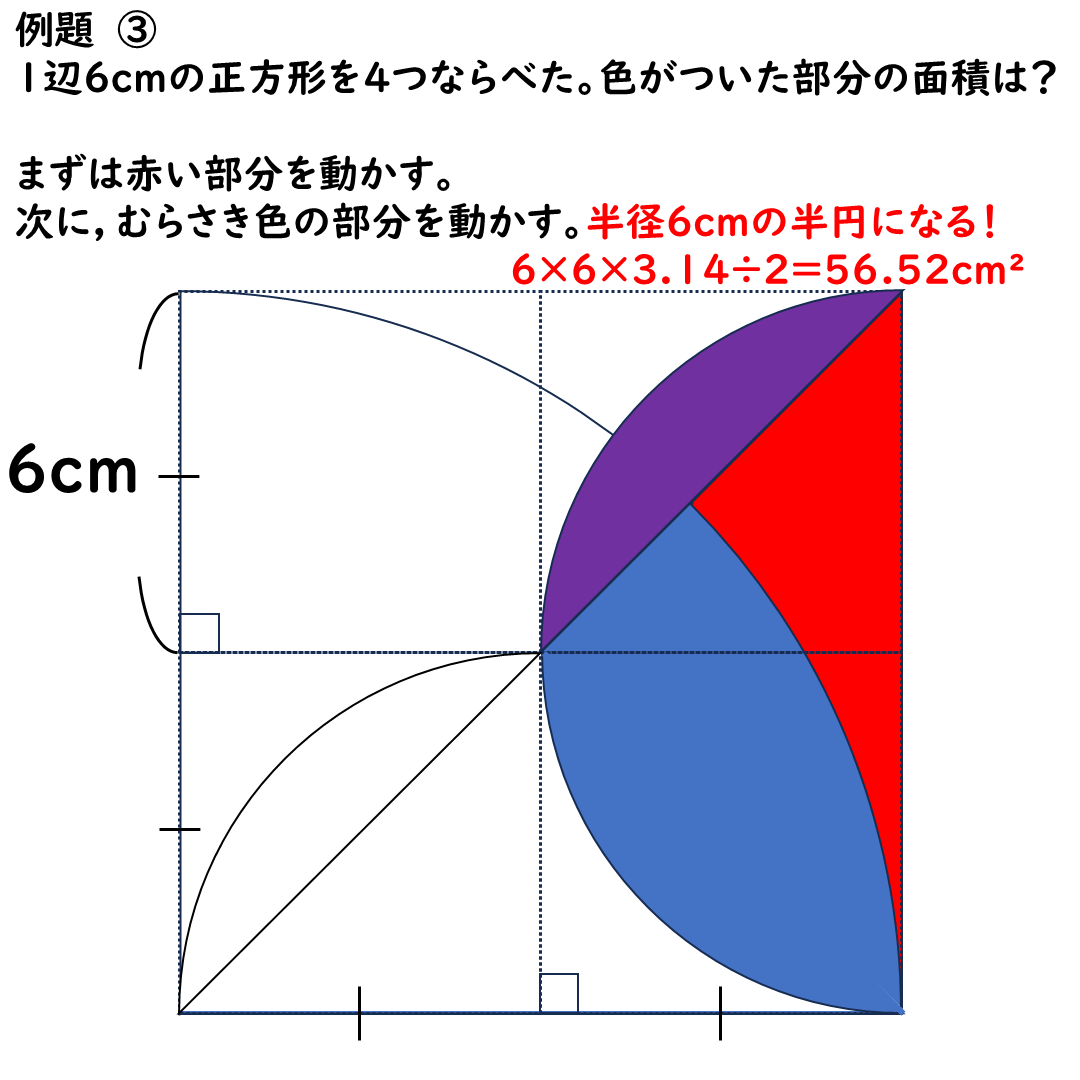
というわけで，

１つ１つ求めるのではなく。

ちょっと立ち止まって

考えてみる，

という問題でした。

保護者の方へのおねがい

お子さんと一緒に解き終わった後，

ああ，やっと終わった終わった。

ではなく。

改めて問題を見返してほしいんですよ。

例えば最後の問題。

もう簡単な問題にしか見えないと

思うのです。

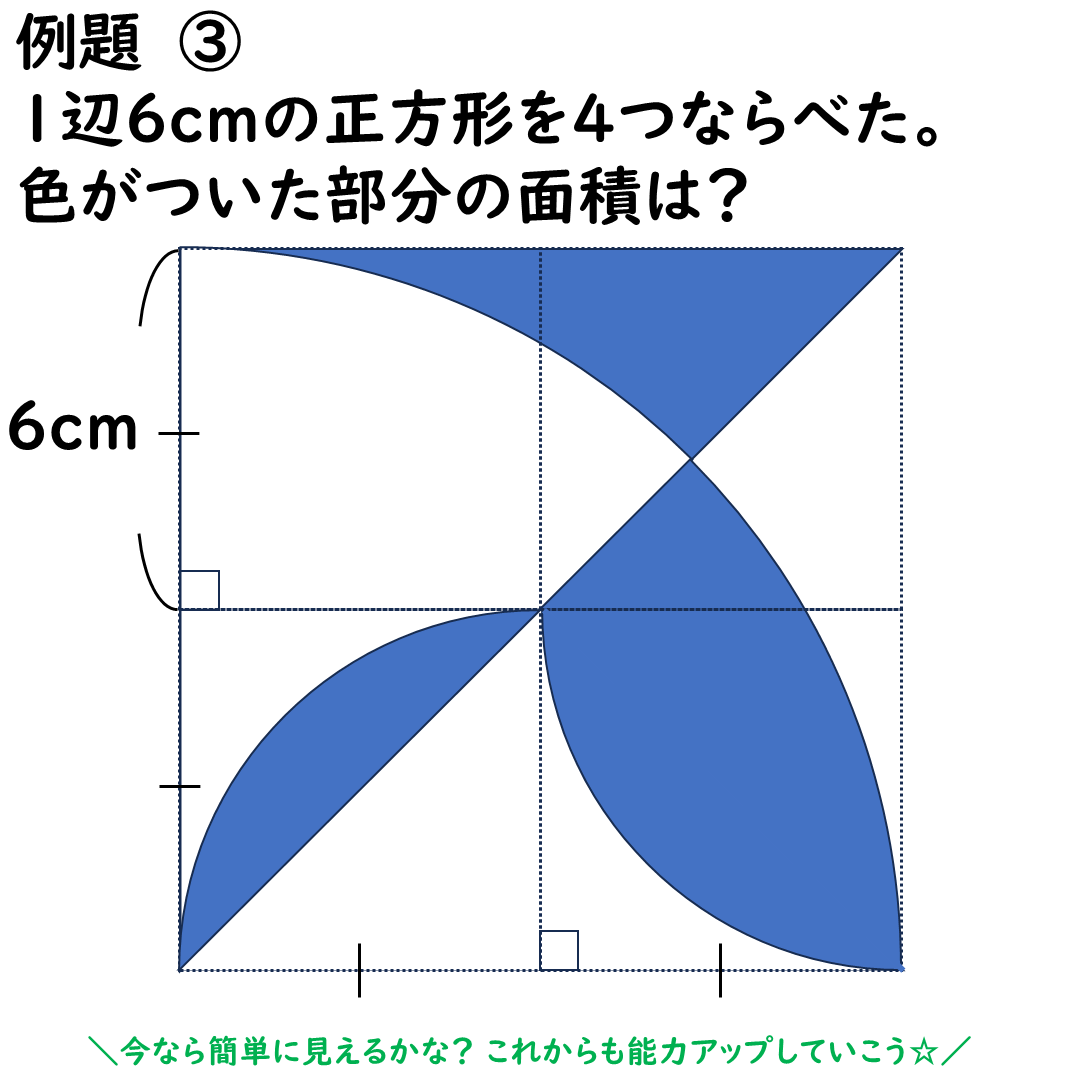
簡単に見えたなら，

問題のチャレンジ前後では

違いがあって，

お子さんは成長しています。

今回，全部で3問を出題しました。

それぞれに工夫のポイントがあり，

単純に解けた！ではなく

新たな見方や考え方が得られること，

学びの楽しさの1つとして

体験してほしいです。

受験とは結局，

どれだけ点数が取れたか勝負ですが，

それだけではただの詰め込み教育。

やるからには，

楽しみながら。

解けなくても

答えや解説から発見があって

今まで知らなかった見方を得て

わくわくする。

私はそれを

親子でリアルタイムで

共有してもらいたいです。