目次
変化の割合を求めよう!
次の問題にチャレンジしてみよう!
<問題>
次の式の変化の割合を
答えよう。
また,
xの増加量が3のとき,
yの増加量も答えなさい。
(1) \(y=3x+2\)
(2) \(y=-4x-5\)
(3) \(\displaystyle y=\frac{4}{3}x+2\)
ヒント
変化の割合は,
答えがそのまま書いてあるよね。
増加量については,
次の式を使うよ。
\(\displaystyle 変化の割合=\frac{yの増加量}{xの増加量}\)
正解はこちら!
<問題>
次の式の変化の割合を答えよう。
また,
xの増加量が3のとき,
yの増加量も答えなさい。
(1) \(y=3x+2\)
こたえ 変化の割合・・・3
yの増加量・・・9
(2) \(y=-4x-5\)
こたえ 変化の割合・・・ー4
yの増加量・・・ー12
(3) \(\displaystyle y=\frac{4}{3}x+2\)
こたえ
変化の割合・・・\(\displaystyle \frac{4}{3}\)
yの増加量・・・4
変化の割合は,\(y=ax+b\) の \(a\) のこと。
傾きとも言います。
式に答えが書いてあるわけです。
次の式は,
変化の割合と増加量の関係です。
これにあてはめることで,
増加量を計算できます。
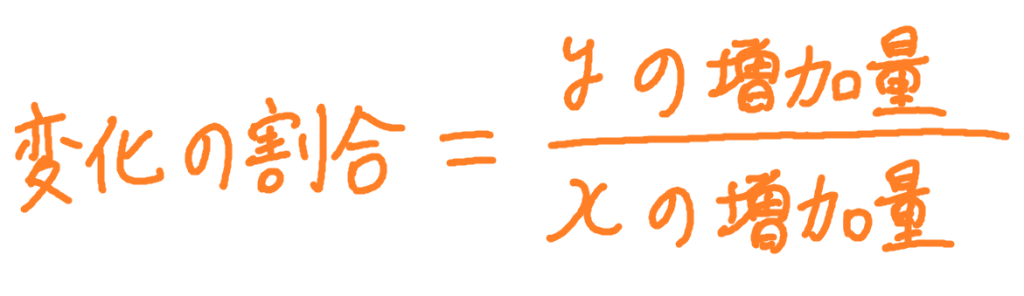
授業動画はこちら!
生徒さんとの解説授業です。
4分16秒です。
ぜひチャレンジしてみてください。