一次関数の式を求めよう！２

一次関数の式を求めよう！２

今回は続編です。

前回はこちらです。

次の問題にチャレンジしてみよう！

＜問題＞次の条件をみたす一次関数の式を求めなさい。

（３）グラフが直線 \(y=4x+2\) に平行で，点（ー３，ー４）を通る。

（４）\(x\) の増加量が３のとき，\(y\) の増加量が５で，点（０，ー１）を通る

正解はこちら！

＜問題＞次の条件をみたす一次関数の式を求めなさい。

（３）グラフが直線 \(y=4x+2\) に平行で，点（ー３，ー４）を通る。

こたえ　\(y=4x+8\)

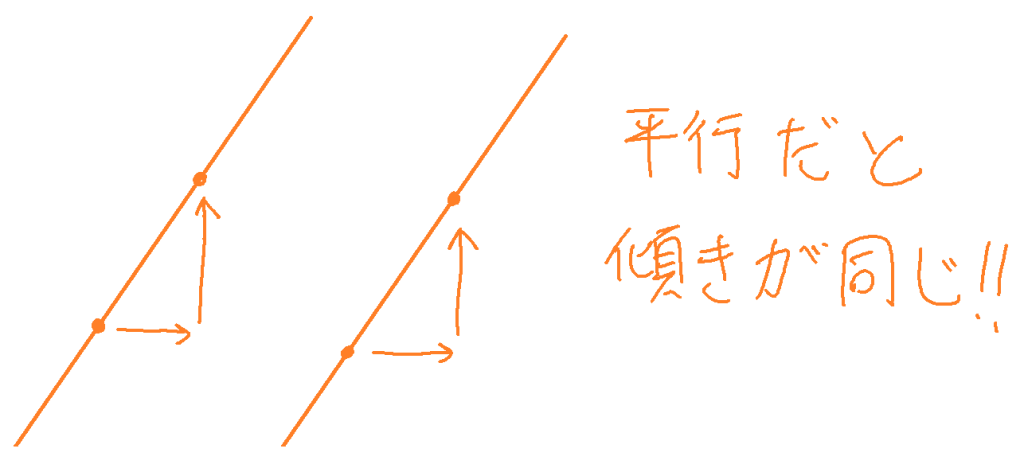
求める直線の式は，\(y=4x+2\) に平行と書いてあります。

その場合，グラフの傾きが同じということになります。つまり，傾きは４です。

\(y=4x+b\) までわかりましたから，あとは点（ー３，ー４）を代入して式を求めていきましょう。

\(-4=4×(-3)+b\) を計算して\(b=8\) 。

（４）\(x\) の増加量が３のとき，\(y\) の増加量が５で，点（０，ー１）を通る

こたえ　\(\displaystyle y=\frac{3}{5}x-1\)

ｘの増加量とｙの増加量が書かれています。

これは，次の関係を使います。

超重要です。

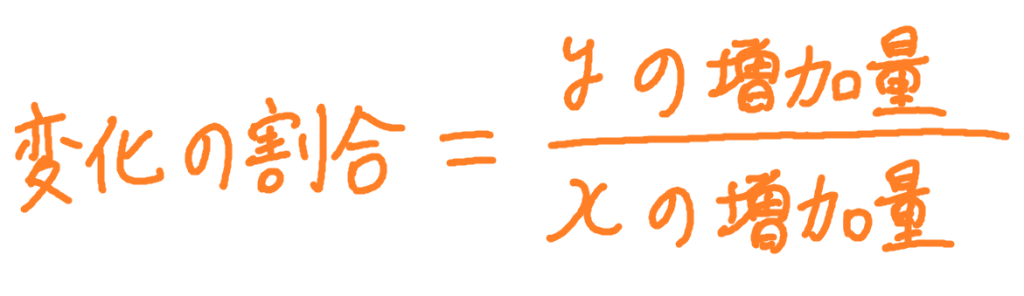
よって，傾き（変化の割合）は \(\displaystyle \frac{3}{5}\) です。

\(\displaystyle y=\frac{3}{5}x+b\) までわかりましたから，あとは切片の点（０，ー１）を入れて完成です。

授業動画はこちら！

生徒さんと一緒に取り組んだ解説授業の動画です。2分12秒です。

ぜひみなさんもチャレンジしてみてください！

おすすめ記事:

一次関数の式を求めよう！ 一次関数の式を求めよう！ 一次関数の式を求めよう！ 一次関数の式を求めよう！ 一次関数を選ぼう！ 一次関数　2直線の交点を求めよう！

最初から1人でやろうとする前に
勝ち方を学んでください。

まずはお声かけください。