平行と合同　正多角形の角度を求める式

正ｎ角形の内角と外角を求める式を考えよう！

 

 

今回のオンライン授業動画はこちら！

 

 

 

 

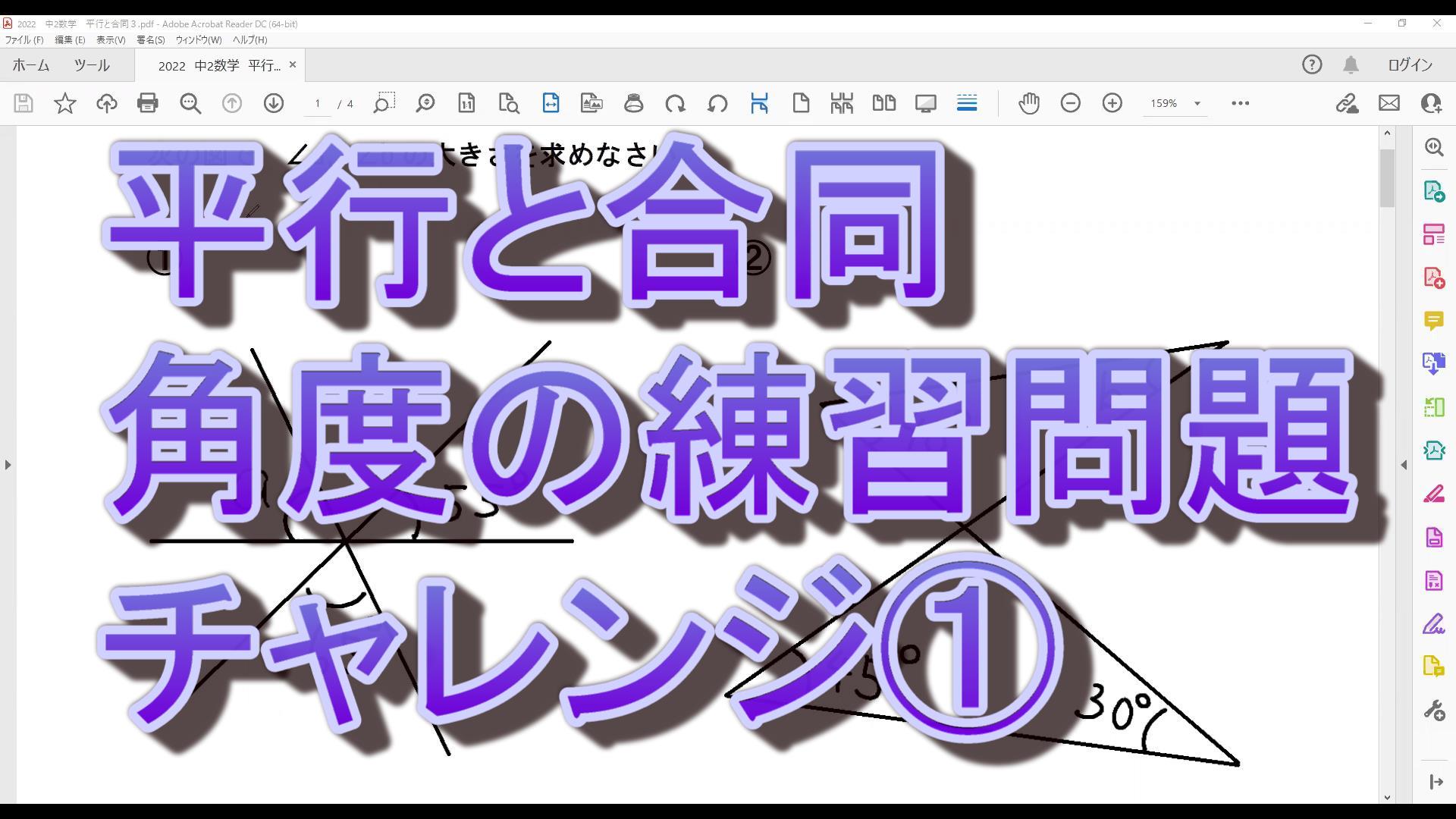
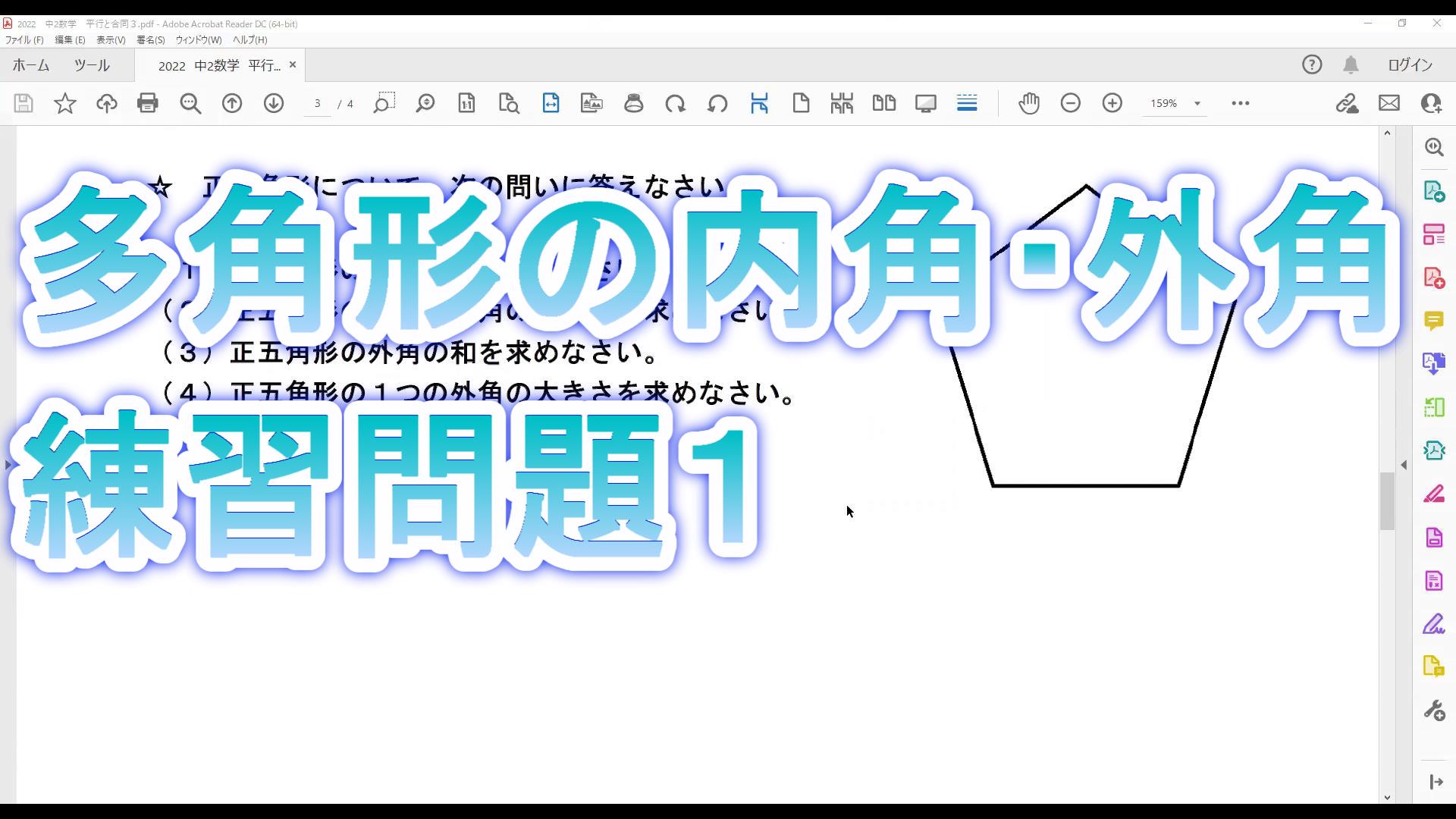
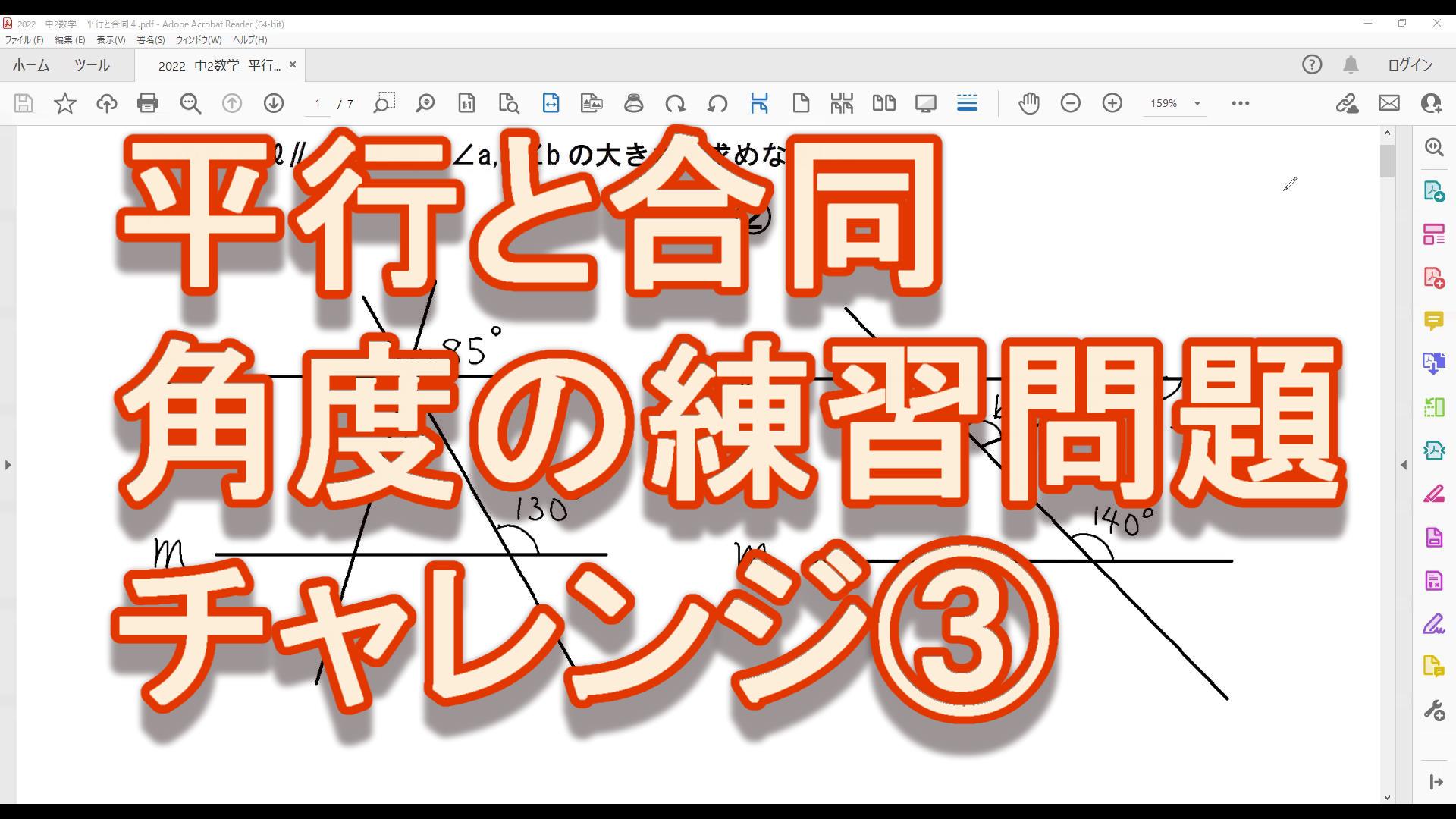
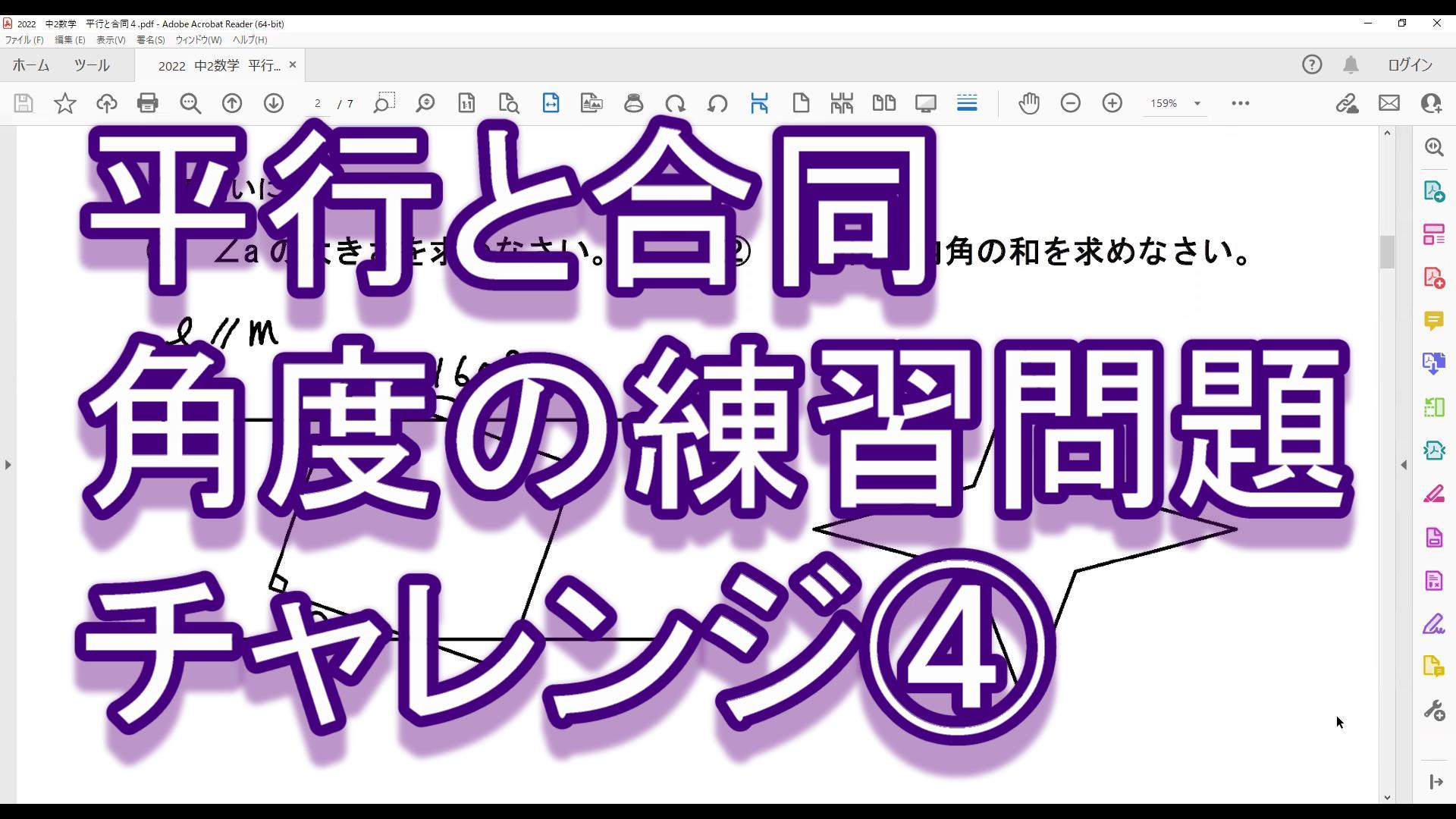
ｎ角形の角度について考える問題です。

 

＜問題＞

次の①～⑤の式は，正ｎ角形の何を表しているだろう？

選択肢があるよ！

 

①　\(\displaystyle 180(n-2)\)

 

②　\(\displaystyle \frac{360}{n}\)

 

③　\(\displaystyle \frac{180(n-2)}{n}\)

 

④　\(\displaystyle 360\)

 

⑤　\(\displaystyle 180-\frac{180(n-2)}{n}\)

 

選択肢

（内角の和　　内角の1つの大きさ　　外角の和　　外角の1つの大きさ）

 

 

 

 

 

 

 

正解はこちら！

 

①　\(\displaystyle 180(n-2)\)

こたえ　内角の和

 

 

②　\(\displaystyle \frac{360}{n}\)

こたえ　外角の１つの大きさ

 

 

③　\(\displaystyle \frac{180(n-2)}{n}\)

こたえ　内角の1つの大きさ

 

 

④　\(\displaystyle 360\)

こたえ　外角の和

 

 

⑤　\(\displaystyle 180-\frac{180(n-2)}{n}\)

こたえ　外角の1つの大きさ

 

 

\(\displaystyle 180-\frac{180(n-2)}{n}\)

\(\displaystyle =180-\frac{180n}{n}+\frac{360}{n}\)

\(\displaystyle =180-180+\frac{360}{n}\)

\(\displaystyle =\frac{360}{n}\)

 

結局，計算したら外角の1つの大きさの式と同じになるよ！

180度から，内角の1つの大きさをひくと，外角が出るよ！

 

 

 

オンライン授業動画も合わせて視聴してみてください！